Table of Contents (click to expand)
Opposite of Infinity is the smallest number there is.
No, the answer isn’t zero. Infinity is the largest number there is, so the opposite of infinity would be the smallest number there is. Zero would mean nothing, so what we’re looking for is a number just greater than zero. However, as we’ll find out, determining this number isn’t as simple as pointing to the number 1.
Recommended Video for you:
Infinities Are Weird
Infinity has baffled humanity since antiquity. One must realize that infinity is not a concrete number, but rather an idea; it exists only in abstraction. Infinity cannot be a concrete number, say, x, because we can, by the logic of addition, add 1 to x and create a new infinity. We can then add another 1 to create a larger infinity. We can, in fact, add infinity to infinity to create perhaps the infinity of all infinities, but then we can add to this infinity another 1 and…you know the drill.

The microscopic realm isn’t any different. The opposite of infinity is called infinitesimal, and its nature is equally bizarre. Unlike whole numbers, real numbers aren’t rigid. Their splintered nature allows us to find and create infinite numbers between any two numbers. A number can be combined as many times as it can be divided. There could be a hundred numbers between 0 and 1, from 0.01-0.99, or even millions, one just has to add zeroes after the decimal point — divide it increasingly to create new numbers. So, while 0.00000000000000001 seems infinitesimal, one can just divide it by 10 to create a new infinitesimal — 0.000000000000000001.
So, infinitesimal, like infinity, exists only in abstraction, yet its uncertain nature is very disconcerting not just for mathematicians, but also physicists.
Also Read: Why Can’t We Divide By Zero?
Infinitesimal Errors
Mathematics is the language we use to express our ideas in physics, so an inconsistency in math translates to an inconsistency in physics, in our knowledge of nature – of reality. The inconsistency arises from our uncertainty of the value of infinitesimal, which has been used to derive many crucial formulae. In fact, an entire branch of mathematics is based on infinitesimal, without which, progress in physics would have been sluggish.
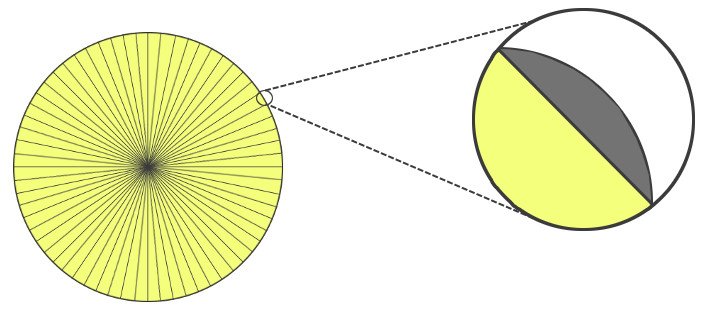
One formula I can think of is the area of a circle. Kepler calculated the area of a circle by dividing it into triangles. The area of the circle, therefore, would be the sum of areas of each triangle. A circle can be divided into four triangles with two diameters, however, the sides of these triangles do not approximate the curves properly, excluding some space, so the area calculated is erroneous.
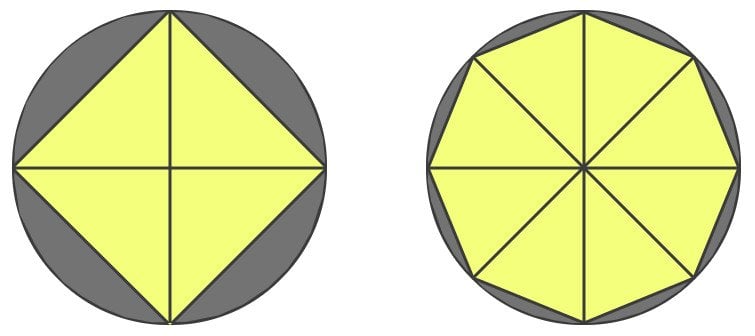
To reduce this error, we can draw more diameters to create more triangles of shorter sides. However, the error is reduced in this way, but it is still finite. So, we further divide the circle into more and more triangles until there is no space left excluded. However, to eliminate this error entirely, we must divide it into an infinite number of triangles. Now, because a line can be interpreted as part of a huge circle, we can say that our circle is composed of infinite lines, which are approximated by the infinitesimal bases of our infinite triangles.
One may notice that the sequence of triangles is reminiscent of a Chinese fan. All the triangles occupy an equal area, but we can convert the fan into a large right-angled triangle by distributing or stretching this area. Their perimeters have changed, but the total area remains the same. The height of this triangle, with the summit being the circle’s center, is the length of the fan — the radius of our circle, and the base, the circle’s circumference. The area is ½ times base times height, which is ½ times r times 2πr, or πr².
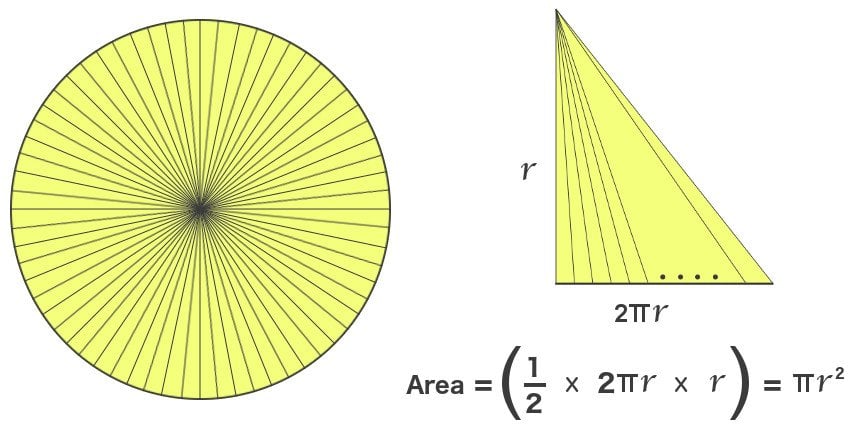
This is, of course, the correct answer, but the outcome is still erroneous. The bases must be truly infinitesimal, so even though Kepler draws really really really thin triangles, we know that he could have drawn more. The moment he stops drawing triangles, he leaves behind spaces, albeit really really really small ones, but still, finite. The curves are then inadequately approximated and the calculation of the area of the circle is slightly erroneous. While this might make a mathematician uncomfortable, the majority “ignore” such differences for, as we have seen, the results procured aren’t incorrect.
Calculus, either invented or discovered by Leibniz and Newton independently, was also founded on infinitesimals. That branch of mathematics is concerned with change, with curves. For instance, when we integrate a function, we essentially calculate the area under the curve it draws. However, like calculating the area of a circle, we calculate it by approximating the curve with infinitesimally thin rectangles. The thinner the rectangles, the smaller the error.
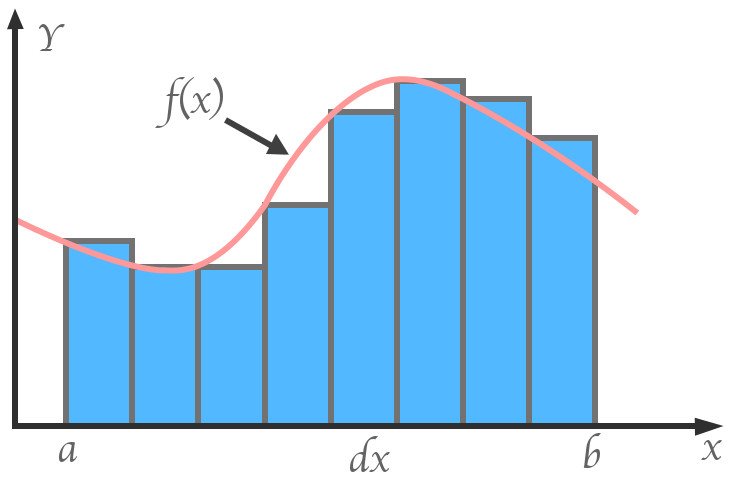
The area of one rectangle is the product of its length — the value on the Y-axis at that point on the curve and its breadth – the infinitesimal unit we call ‘dx’. We calculate the area of each rectangle and sum them to determine the area under the curve. This is very useful in physics; for instance, the area under the velocity curve of a body gives the value of its displacement, but then shouldn’t the outcome be erroneous, just like the area of the circle was?
This ineradicable, insoluble problem bothered mathematicians for two centuries following the advent of calculus until the concept of limits was refined. Limits were implicit in Newton and Leibniz’s work, but they were modified and redefined later in the early 1800s. The new ideas were mathematically rigorous and consistent. The details are beyond the scope of this article, but limits allowed mathematicians to finally get rid of infinitesimals for good. What we still haven’t gotten rid of is the absurdity that is infinity.
Also Read: Can The Area Of A Circle Ever Be Exactly Determined Since Pi Goes On Forever?