What Are Imaginary Numbers? Why Are They So Important?

Imaginary numbers are numbers that are multiplied by the imaginary unit ”. They are important because they allow us to solve equations that would be unsolvable without them.

Imaginary numbers? As if the numbers we already have weren’t enough. The commentary on mathematics’ difficulty has become a platitude. We’re all aware that some proportion of all high schoolers are terrified by the unintelligible language their math textbooks are scribbled with, like Victorian readers encountering Ulysses for the very first time.

However, rather than experiencing relief, their terror is only exacerbated when the turn of a thin page marking the end of another arduous chapter introduced them to an entirely new dimension of numbers – imaginary numbers. Eventually, the introduction of imaginary numbers opened our eyes to an entirely novel branch of mathematics, another of nature’s absurd languages – complex mathematics. Why are they so significant if they’re not even real?

Recommended Video for you:

“Impossible” Numbers: What Are Imaginary Numbers?

If the number 1 is the unit or identity of real numbers, such that each number can be written as that number multiplied by 1, then imaginary numbers are real numbers multiplied with the imaginary identity or unit ‘‘.

The imaginary unit represents a clever way around a mathematical roadblock. Consider the simple quadratic equation . The value of  for which the sum becomes zero must be a number whose square is -1. But that is impossible! Squares of all real numbers, either positive or negative, can only be positive numbers. In other words, the problem has no real number solution.

Even so, let’s solve for  anyway. The solution turns out to be . There is the roadblock – negative numbers don’t have a legitimate square root. This indivisible unit  is denoted by , such that the solution to the given equation becomes . All numbers multiplied by this unit have come to be known as imaginary numbers. The unit can be used to derive the solutions for other similar quadratic equations. Consider . Here,  turns out to be , which can be written as .

Witnessing this, impossible is the first word that would pop into anyone’s mind. The square root of negative numbers is highly counterintuitive, but so were negative numbers when they were first introduced. Even Euler was confounded by them. So, don’t worry if you can’t wrap your head around imaginary numbers; initially, even the most brilliant of mathematicians couldn’t.

The incredulity results from, of course, the denial of the comfort of certainty that we find in rituals to which we are indelibly accustomed. Imagine the astonishment of the Romans when they were introduced to Base-10 numbers. Or, the infinite numbers between them. If zero, or a symbol, a “something” to describe “nothing” wasn’t enough, the concept of negative numbers was introduced – numbers that represent a quantity less than nothing. This was a Roman’s worst nightmare. Despite their horror, we needed these new systems… all of them.

The existence of equations that are unsolvable in a single system is quite common. With only natural numbers,  would be unsolvable, unless we introduce integers. Now, despite the knowledge of both natural numbers and integers, the equation  would be unsolvable without introducing rational numbers. The equation  would be unsolvable without irrational numbers. And finally,  would be unsolvable without imaginary numbers.

One would assume that imaginary numbers arose from our need to solve quadratic equations, but their existence was actually hinted at by a cubic equation. One of the oldest and most popular problems that involved them was “To divide 10 into two parts, the product of which is 40”. This was solved by Girolamo Cardano, who divided 10 into two equal parts of 5. He squared them (25) and subtracted 40 from it, which left him with -15. He concluded that the square root of -15 added to or subtracted from 5 gives two parts, the product of which is 40.

Doesn’t make any sense? This would be much easier to understand if the operations were written this way: . A quick calculation would transmute this product into a simple subtraction: 

Now, because  (for simplicity, let’s ignore the other root: ) the operation becomes a sum:

Also Read: What Is I Raised To The Power I?

What Are Complex Numbers?

Subsequently, in 1572, the mathematician Rafael Bombelli published his treatise on algebra, which expounded the nature of imaginary numbers in splendid detail. This made him a central figure in the understanding of complex numbers. Complex numbers are a combination of both real and imaginary numbers. A complex number Z is the sum or subtraction of a real number A and an imaginary number Bi, such that .

Despite this work of genius, Bombelli’s book was frowned upon. The numbers were dubbed fictitious – or even useless – by his peers. Descartes referred to them as imaginary in a tone that verged on ridicule. The numbers accrued acceptance when Euler and Gauss began to recruit them in their work. Other mathematicians gradually caught up and realized how immensely important they are, that these numbers fill an empty void in the subject. However, Descartes’ slur stuck, and we continued to refer to them as imaginary to this day.

In a way, every number seems fictitious. This is the central argument in the debate of whether math was discovered or invented. The Romans invented their system to count whole, countable things, such as to keep count of the number of elephants they lost in a war. The process can be roughly translated to: “Let us represent this exclusive set of elephants with this symbol. The introduction of a new elephant will transform this set into a new, different, exclusive set which can be represented by another symbol and so on.”

In that case, what do negative numbers entail? One can say that a negative number is a highly convenient way to limn debt. Without negative numbers, quantifying debt would have been extremely difficult. Similarly, complex numbers represent rotation. This renders them ubiquitous in branches of physics that involve vectors and waves, such as the laws of electromagnetism and Fourier Transform, an indispensable tool that we use to analyze music.

The new dimension I mentioned in the prelude is real. There is a plane solely dedicated to plotting complex numbers known as the complex plane. To understand what I meant by rotation, let’s step into this new dimension. A complex plane is a 2D plane on which real numbers are plotted on the horizontal axis, known as the real axis, and complex numbers are plotted on the vertical axis, known as the imaginary axis.

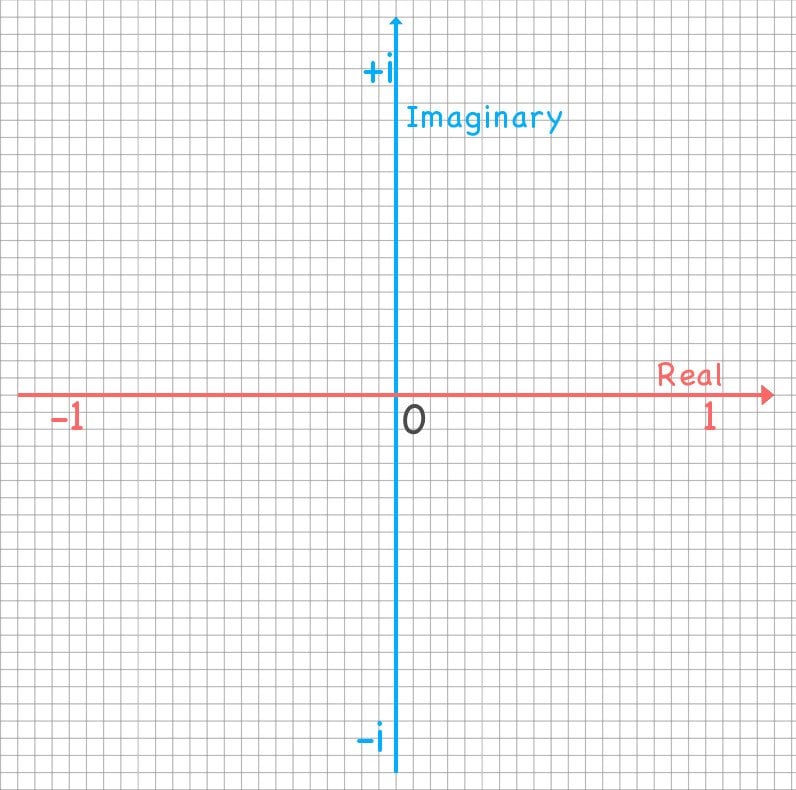
A peculiar pattern can be observed each time we multiply a real number with . Graphically, the product represents a counterclockwise rotation of a vector of size  by 90º each time an  is multiplied to it. If we assume the value of  to be 1, only 4 vectors repeatedly emerge:  and ; a quarter of a circle, a semi-circle, a three-quarter circle and a full circle.

However, if we were to rotate this vector by, say, only 45º, the resulting vector would lie in the middle of the two axes; the area it sweeps represents a small part – in this case, exactly one-eighth of a circle. A 45º line implies the equivalence of coordinates or, as it is popularly known, the  line. If one such coordinate is (A, B): (1,1), then one can conclude that the drawn vector represents the complex number .

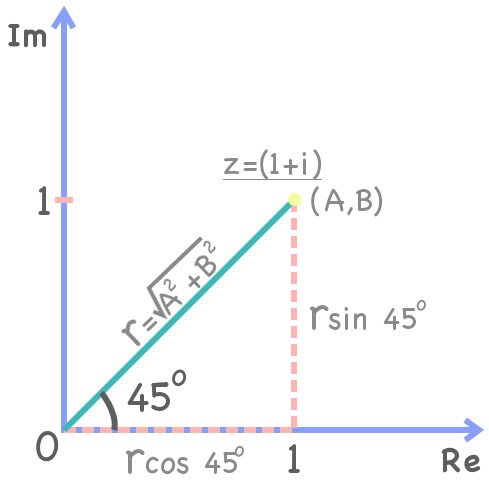
The same vector can also be represented as a vector sum of its horizontal and vertical components — . Here,  is the hypotenuse of a triangle formed by the vector and its perpendicular components and  is the angle the vector makes with the horizontal axis. The modulus ’s value is the Pythagorean sum of the two components. This property binds trigonometry and complex numbers in a conjugal relationship, rendering them utterly inseparable.

No wonder they are so ubiquitous in electronics and wave theory. This characteristic illustrates how deeply rotation is ingrained in complex numbers. This makes for efficient problem solving, problems that concern rotation, problems that would have been troublesome or tedious when tackled with conventional math – doable but inefficient. However, personally, their most commendable achievement remains their direct involvement in the formation of one of the most beautiful structures in abstract math, one of the most beautiful sentences written in nature’s languages.

The curve drawn on a complex plane, known as the Mandelbrot set, looks like an enormous garden that comprises a long nonlinear trail of infinite coniferous trees and spiraling flowers. It is absurd how the menial act of simply plotting coordinates can lead to such an aesthetic marvel. It is a visual treat for Mandala artists, a true testimony to splendor and detail. And remember, all of this came from imaginary numbers. Math never ceases to amaze me.

Also Read: Is There Anything More Complex Than Complex Numbers?