How Were Irrational Numbers Discovered?

In the 5th century BC, the philosopher Hippasus discovered that some numbers could not be expressed as a ratio of two different numbers, and thus were irrational. This discovery contradicted the Pythagorean belief that everything could be understood through numbers, and as a result, Hippasus was killed by the Pythagoreans.

Mathematics is the science of numbers, and just like any other form of science, it is constantly evolving. However, changes in scientific thought are not always welcome, since they contradict the popular belief, even though in most cases, the popular belief is wrong. In a similar fashion, the discovery of irrational numbers challenged the established doctrines of numbers and expanded the world of mathematics forever.

In 5^th century BC Greece, Hippasus was noted as one of the earliest revolutionaries. He was an Italian philosopher who was also a member of group of people who were called the Pythagorean Mathematicians. They believed that “All Is Number”, which meant they had a religious reverence for mathematics and suggested that numbers were the building blocks of the universe.

According to them, everything could be understood through the language of numbers. Be it the movement of stars in the night sky, the music that we listen to, or even the moral decisions of the people. The mathematicians claimed that everything always followed eternal rules and naturally felt threatened when these rules were questioned.

Recommended Video for you:

What Are Rational And Irrational Numbers?

Our earliest basis for numbers and math derives from the practical need to count and measure things. It is intuitive to see how the positive, non-zero, natural numbers would arise “naturally” from the process of counting. Even fractions are easy to comprehend, due to the need to divide measurable quantities into smaller parts. However, the group of philosophers was traditionalist and their understanding of numbers was based on the fact that every number could be represented as a ratio of two different numbers that had no common divisor except 1. For example, 24 could be represented as 24/1, while 0.6 could be represented as 3/5.

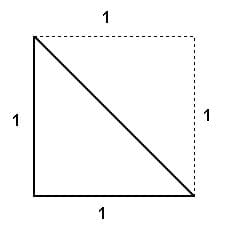
These numbers are known today as rational numbers. The name ‘irrational numbers’ does not literally mean that these numbers are ‘devoid of logic’. Any number that couldn’t be expressed in a similar fashion is an irrational number. Such a number could easily be plotted on a number line, such as by sketching the diagonal of a square. Although people were aware of the existence of such numbers, it hadn’t yet been proven that they contradicted the definition of rational numbers.

What Did Hippasus Do?

Hippasus is credited in history as the first person to prove the existence of ‘irrational’ numbers. His method involved using the technique of contradiction, in which he first assumed that ‘Root 2’ is a rational number. He then went on to show that no such rational number could exist. Therefore, it had to be something different.

The reason that he chose ‘Root 2’ for his calculations is two-fold. Firstly, it is the easiest technique to prove the existence of irrational numbers. Secondly, it has a great significance for Pythagoreans. Pythagoras had himself proven that the sum of squares of the sides in a right triangle is always equal to the square of the hypotenuse.  For the simplest right-angled triangle, which is of unit base and unit height, the length of the hypotenuse is ‘Root 2’. However hard he might try to express this as a ratio, he failed. Instead of giving up, he decided to prove that it couldn’t be done.

Method:

1. He first assumed that ‘Root 2’ is a rational number. Since every rational number can be expressed as a ratio, then according to his assumption, even ‘Root 2’ could be expressed as p/q, which is a ratio. Here, p and q are integers and DO NOT have any common factors except 1, which is how we define the lowest form of a rational number representation. For example, 2 could be represented as 4/2 or 6/3, but as a rule, it is represented by its lowest form 2/1.
2. Next, he said that since q isn’t zero, it could be multiplied on both sides.
3. If both sides are squared, 2(q)²=p²
4. We know that squares of odd numbers always give an odd number, whereas the square of an even number always gives an even number. For example 5²=25, 31²=961, 52²=2704 etc. Since q is an integer, p would have to be an even integer, since it is equal to 2 times q². Hence, p could be replaced by 2x, where x is any integer, so that 2x is always even.
5. On replacing p with 2x in the equation, we obtain 2q²=4x² or q²=2x². This implies that q is also an even integer, since it is 2 times x².
6. Interestingly, the initial condition was that p and q could not have any common factors. However, through simple algebra, we seem to have arrived at the conclusion that both p and q are even integers! If they are even, they would always have 2 as a common factor, which contradicts our condition.
7. This implies that our initial assumption of ‘Root 2’­ being a rational number is false and therefore has to be irrational.

Why Did They Kill Hippasus?

The discovery of irrational numbers could have changed mathematics as the world knew it back in 5^th century BC, but change doesn’t come easy for traditionalists, even more so for fanatics! They considered his discovery to be a ridicule of the absolute truth, and condemned him to death. He was flung into the sea and his work was destroyed. Some believe that the Pythagoreans were so horrified by the idea of irrationality that they threw Hippassus overboard on a sea voyage and vowed to keep the existence of irrational numbers a secret.

Basically, he was wrongfully punished for a crime that brought mathematics to a new frontier by people who were supposed to be pursuing the same goal. Ancient Greece sounds like a pretty ironic place…