Is There Anything More Complex Than Complex Numbers?

There are multiple number systems in mathematics that are more complicated than complex numbers, such as the quaternions.

When we were kids, the only numbers we cared about were the ones we needed for counting. How many eyes do you have? Two! How old are you? Seven! How many candies do you want? Well… countless, but you get the gist.

We did not need numbers other than those used for counting things because they seemed to naturally appear in nature, and thus, the natural numbers were born.

As you grew up and failed more and more tests, you came to understand the importance of zero. You ended up adding this zero to your existing set of numbers and got whole numbers.

Things kept getting more complicated. At some point, you met negative people in life who introduced you to the concept of negative integers.

There were also rational and irrational people who let out a bombardment of completely weird kinds of numbers on you.

However, this was all okay because you knew they were all real, but the happiness was short-lived. The numbers got you so bad that soon enough you were imagining them. You just couldn’t keep up because they kept getting more complex, and eventually you just sat down and wondered, “Is this ever going to end?

These complex numbers seem pretty complicated, right? Can I stop there or is there something even more complex than complex numbers?”

Spoiler alert: Yes, there is something even more complicated… and it gets worse.

Recommended Video for you:

What Are Complex Numbers?

Let’s look at imaginary numbers first. What is an imaginary number and what makes it imaginary? First of all, imaginary numbers are not included in the set of real numbers. Real numbers consist of all the integers, as well as rational and irrational numbers.

Now, you might feel like real numbers contain all the numbers there are, but that’s not quite right. Think about this, what is the square root of 4? You know the answer to this, right? It’s either 2 or -2 (because both numbers, when multiplied by themselves, give the same number).

Fairly easy, right? Now try this, what is the square root of -4? Let’s think about that. What number when multiplied by itself, gives -4? The answer can’t be 2 or -2 because you need to multiply them with each other and not themselves (since 2 and -2 are two completely different numbers).

What we use at such times is an imaginary number i. The value of i is  (making ). Thus, we can write that the square root of -4 is 2i. Any number when paired with i becomes an imaginary number.

A complex number is a combination of a real number and an imaginary number. It has the form:

Complex Number = Real Number + Imaginary Number

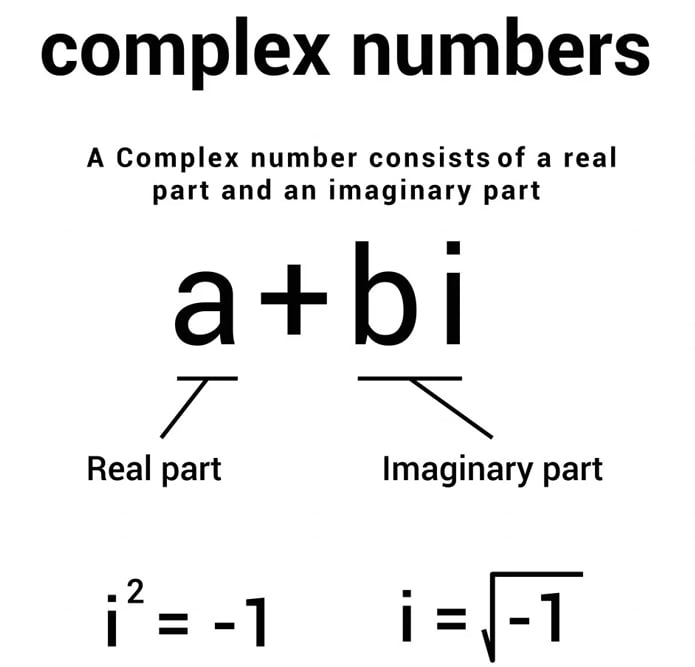
For example, we can have a complex number 4+3i, where 4 is the real part and 3i is the imaginary part.

How Do Complex Numbers ‘Rotate’?

Let’s first imagine these numbers on a graph. Ever since we were kids, we have been taught the number line. A number line can show all the real numbers from  to .

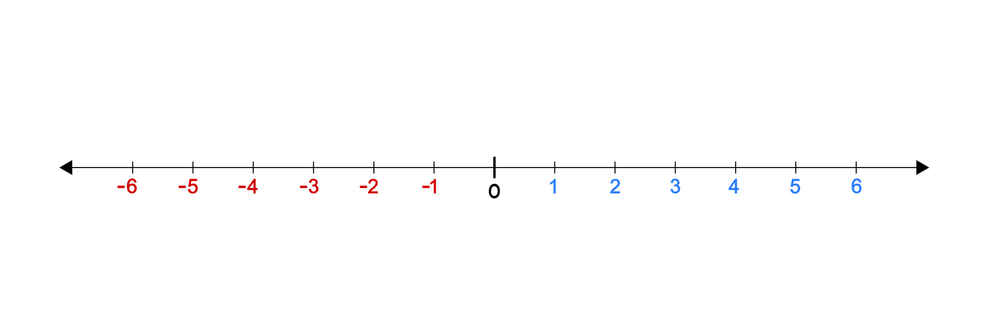
You see, a line is just 1-dimensional, so you only need one dimension to represent the real numbers. One can also say that real numbers are 1-dimensional.

Now, let’s see how we can represent complex numbers. As mentioned earlier, complex numbers have two parts—one real and one imaginary—so in order to represent them graphically, we need two lines, one line for the real part, just as before, and one line for the imaginary part, in the units of i.

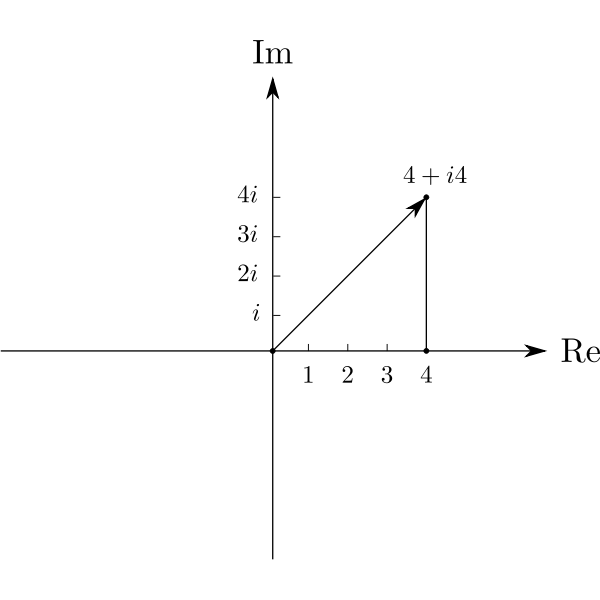
Thus, complex numbers need two lines or axes to be represented graphically, so they are 2-dimensional, and there is one very interesting thing you can do in two dimensions… rotate!

On a straight line, we can move only forward or backward, but in a 2-D plane, we can move up-down, left-right, or even mover in a complete circle by rotating 360 degrees.

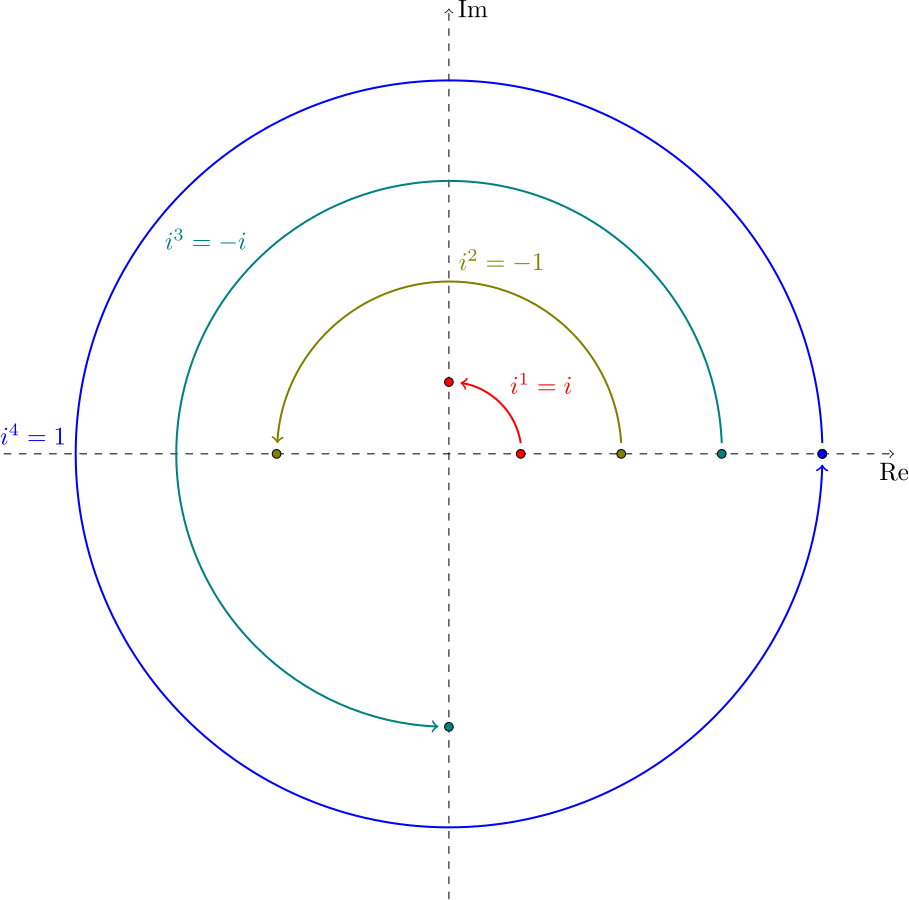
We can move on the horizontal axis by adding or subtracting a real number and we can move on the vertical line by adding or subtracting an imaginary number, but if we multiply a complex number by i, then we end up rotating the number (it’s like picking the number and moving it on the perimeter of a circle and then placing it at some other angle) through a certain angle.

So How Do You Rotate In 3 Dimensions?

That exact question was troubling William Hamilton while he was on a walk with his wife. He was hit with the sudden realization that a 4-dimensional number would solve the issue.

It is believed that he carved the first rule of his new 4-D numbers, known as Quaternions, right there on the Brougham bridge, which is:

This is very similar to the  rule seen for the imaginary numbers.

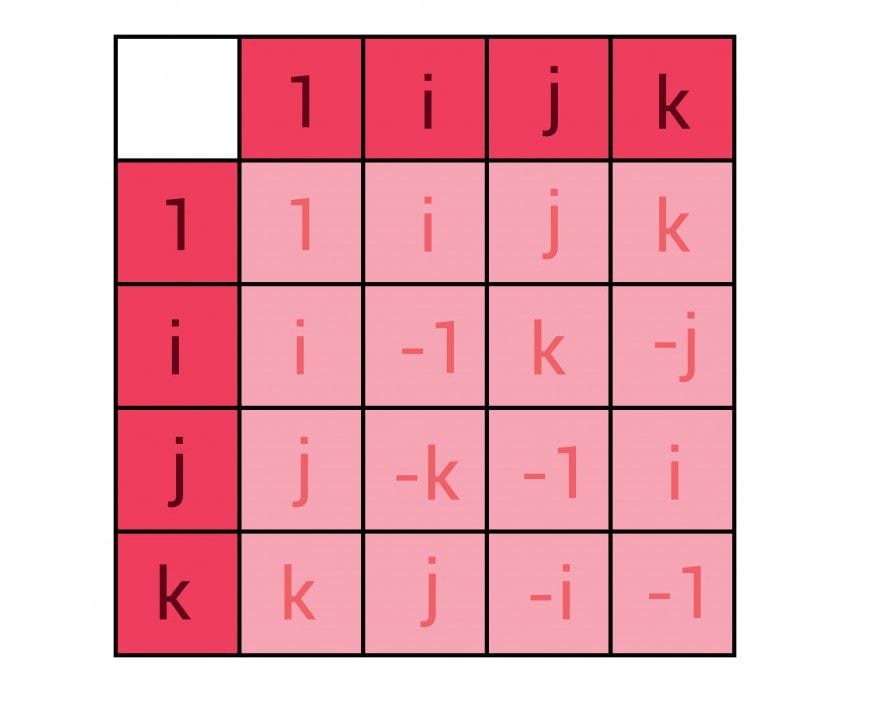
And just like complex numbers, a quaternion is written as a combination of these numbers, along with a real number, for example: 6+2i+4j+7k.

As we have seen in the 2-D case of complex numbers, multiplication by i rotates the number in the 2-D plane; in the case of quaternions, multiplication by any one of i, j, k, or combinations of them rotates a number in 3 dimensions.

This is an extremely important property of quaternions that is used in graphics programming to make animated objects rotate in their environment. In fact, quaternions are also used to map and program the rotation of your smartphone and tablets.

Conclusion

So yes, there are more complex number systems than the complex numbers, one of which we saw here in the form of quaternions—the 4-dimensional numbers. There are even systems of 8-dimensional and 16-dimensional numbers, but they’re not very useful and are therefore hardly ever discussed (even in hardcore mathematics groups).

While things do get much more complex than complex numbers, you don’t have to worry about that. We’re more than happy with our small group of real numbers, because they will always be our real friends.