What Is Imaginary Time?

Imaginary time is a mathematical simplification of time that is used in several equations across quantum mechanics and general relativity.

What happened at the beginning of the universe? Most people would simplify and say that there was a Big Bang and then everything spontaneously burst into existence. That statement certainly has an element of truth, to some extent.

However, what exactly happened at the beginning of time itself? And what happened before that? Questions like these have eluded the scientific community to this day.

When we start to look at things at the beginning of the universe, or even before the beginning, nothing is what it seems. The math gets fuzzy, the physics gets hazy, and conventionally accepted “truths” tend to fall apart.

How would one even begin to understand the universe at a time so close to the beginning (t=10^-33 seconds)? That number has thirty-three zeroes after the decimal point! Trying to solve problems in physics at that stage of our universe’s lifecycle gets incredibly tedious. Actually, tedious might be an understatement… it gets downright impossible!

This impossible nature is primarily because, close to the very beginning of time, we approach what is called a singularity.

A singularity is the theorized state of the universe prior to the Big Bang. As we get closer to a singularity, the conventional laws of physics begin to break down. The scientific community needed a workaround for this. How would they analyze the state of the universe that close to the beginning without dealing with the pesky, physics-bending singularity?

Enter… imaginary time!

Recommended Video for you:

What Is Imaginary Time?

Simply put, imaginary time is a mathematical simplification of time used in several equations across quantum mechanics and general relativity.

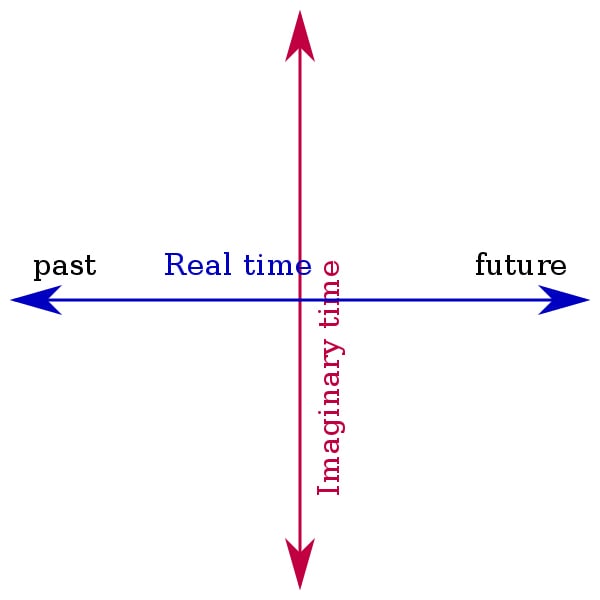
Think of real-time as a horizontal line. A single point on that line is a moment in time. To the left of that point is the past and to the right is the future.

Now imagine a second line perpendicular to real-time. This essentially represents imaginary time. Being perpendicular to real-time, it allows for everything to occur all at once. Since humans can only perceive single moments in time, wrapping your head around ‘imaginary time’ may prove difficult.

However, by allowing for everything to happen simultaneously, we’re able to avoid the idea of a beginning. Without a starting point, imaginary time becomes something that has always been in existence. There is no boundary from where ‘imaginary time’ started. In imaginary time, there was no big bang and hence, close to the beginning of real-time, imaginary time still remains very much like any other point in time. There is no fuzzy physics or hazy mathematics. There is no occurrence of that pesky singularity.

The concept of imaginary time may not immediately seem useful or easier to visualize, but mathematically, it becomes a physicist’s best friend when he or she is tired of dealing with singularities in all their calculations.

So how do we create this convenient perpendicular line of time? Do we arbitrarily sketch a line anywhere in space and call it ‘imaginary time’? I wish it were that simple, but when dealing with four-dimensional space-time, “simple” is seldom on the menu, so let’s begin.

How Do You Convert Real-time To Imaginary Time?

The three dimensions of space, along with the dimension of real-time, form what is known as Minkowski’s spacetime. By incorporating all four dimensions, Minkowski’s spacetime becomes an area where one can plot anything that occurs in the universe simply by specifying its time and spatial orientation.

Of course, visualizing four dimensions is no easy feat. Some of the numbers may make mathematical sense, but don’t physically translate well. Moreover, there is also a boundary, which can be a cause for alarm that we discussed earlier.

Minkowski’s spacetime must be altered to make it simpler. For this, we can translate the complexity of Minkowski’s spacetime into conventional geometrical space, which makes it easier to understand and solve for. This geometrical space is known as Euclidean space.

Wick Rotation

The translation is done using what’s known as Wick’s rotation. This involves substituting the component of time in Minkowski’s space with the value for ‘imaginary time’. This involves multiplying the value of real-time by √−1, which is an imaginary number denoted by ‘i’. 

Remember the flat line of real-time we discussed earlier? By multiplying the value of real-time by ‘i’, we are essentially rotating that line and turning it into a perpendicular. Once we convert Minkowski’s space into Euclidean space by rotating the time axis, we are left with space that lacks a boundary, and thus lacks any scope to contain a pesky singularity. Once we solve whatever we need to solve at a time close to the Big Bang, we can then resubstitute the values, i.e., undo Wick’s Rotation and find the final result in real spacetime, i.e., Minkowski’s spacetime.

Use Of Imaginary Numbers In Science

However, the use of “imaginary” time met with some resistance from the scientific community. In fact, an entire section of the community has long been at war with ‘imaginary’ numbers altogether. They basically believe that it is a ridiculous notion. How could any number representing a real quantity be imaginary?

If we said that, where would the imagination end? Why not just make everything imaginary? A whole world made of imagination. A sort of Wonderland, perhaps with a girl named Alice exploring it for an inexplicable reason. Do we even need a reason? That could be imaginary too! We could suggest that a little rabbit caught her attention, so she followed him down a rabbit hole.

Alice In Wonderland

In fact, this is very close to the true origin story of Alice in Wonderland. The original story published in 1865 was written by Lewis Carroll, a pen name adopted by a mathematician of the era by the name of Charles Dodgson. Dodgson did not believe that it was justified to use imaginary numbers in mathematics.

He considered the notion to be utterly irresponsible. The original takeaway from his story was the sheer ridiculousness of a world with imaginary entities.

Think back to the Mad Hatter’s tea party. There have been several versions of this scene over the years, but every version stayed true to one attribute—the party was outrageous. It was a party where it was always tea-time, no matter the time, because time had left the room. According to Charles Dodgson, the whole world would eventually turn into a massive Mad Hatter’s tea party if imaginary numbers had their way.

On the other end of the spectrum sat one of the most brilliant minds in modern physics, Stephen Hawking. In Hawking’s book, The Universe in a Nutshell, buried deep among the pages of wisdom is a special nugget concerning ‘imaginary time’.

He stated that several mathematical models incorporating the variable for imaginary time are also able to predict a certain phenomenon that we can already observe in the universe. Of course, this begs the question… how imaginary is ‘imaginary time’?

If it’s able to make accurate ‘real-world’ predictions, doesn’t it warrant the title of ‘real’? Rather than being relegated to little more than a mathematical simplification, Hawking argued that perhaps it’s time to reconsider our perspective of time itself. ‘Imaginary time’ may indeed be just as real as our narrow perception of linear time.