Table of Contents (click to expand)
Quantum mechanics is the branch of physics that studies the behavior of matter and energy in the presence of an observer. It is the foundation of modern physics and the theory of the wave-particle duality.
Legendary Nobel Prize-winning physicist Richard Feynman famously quipped that if you think you understand quantum physics, you don’t understand it at all. Although it was said in jest, we have since come a long way in our understanding of quantum mechanics. It is due to this understanding that we have been able to make significant technological leaps, such as the invention of the computer, lasers, digital cameras and nuclear power plants, just to name a few. Without a sound understanding of quantum mechanics, could we have even dreamed of controlling something as unpredictable as nuclear power? To dive into a deeper understanding of quantum mechanics, let’s first look at the three fundamental pillars upon which quantum mechanics is built.
Recommended Video for you:
The Three Pillars
Quantum Mechanics is a subject that was developed slowly, over many decades. Its origins began with a set of controversial mathematical explanations for controversial experiments that did not fit within the capabilities of good old classical mechanics to explain. In the 20th century, around the same time Albert Einstein was releasing his theory of relativity, a separate mathematical revolution was taking place in the physics realm concerning the motion of things at very high speeds. High speeds is a rather vague distinction, but in this, we assume it to be concerned with things traveling close to the speed of light. Unlike the theory of relativity, the birth of Quantum Mechanics cannot be attributed to one person. It was a combination of multiple scientists who laid down the three foundational pillars of QM (an abbreviation of Quantum Mechanics).
The first of these principles is Quantized Properties. Quantized properties give the position, speed, color and other properties of a particle that can sometimes only occur in specific set amounts and instances. This was very different from the notion of classical mechanics of that time, which said that such properties should exist in a smooth continuous spectrum. This was something that scientists found to be unique and soon coined the term quantized particles. The next pillar of the field was the particle nature of light. The notion that light could be a particle was initially met with colossal criticism, as it ran contrary to the well-established line of thought that light behaved in the form of waves, which scientists had concluded after numerous experiments proving the wave nature of light. The wave nature of matter is the final conceptual pillar on which Quantum Physics was built. Whether you can wrap your head around it or not, matter also tends to show wave-like properties. Again, this was a surprise for most people, as this was contrary to all scientific experiments conducted up to that point. Now, let’s take a look at these three pillars of quantum physics in more detail.
Quantized Properties
In 1900, German Physicist Max Planck wanted to explain the distribution of the colors emitted over the spectrum in the glow of red-hot and white-hot objects. A classic example of this relates to light bulb filaments. In the event of trying to formulate the equation that would describe this formula, Planck went on to mathematically explain the distribution of the colors. Planck realized that this distribution implied that combinations of certain colors (albeit a considerable number) were emitted. The colors that were emitted also showed a strange peculiarity, wherein the emitted colors were a multiple of a base value. Somehow, the colors appeared to be quantized!
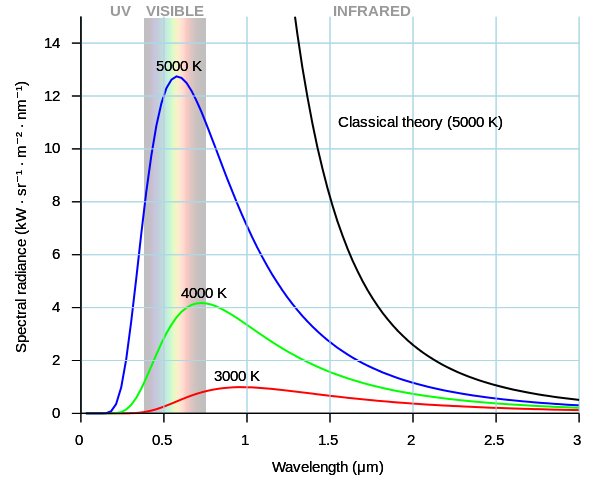
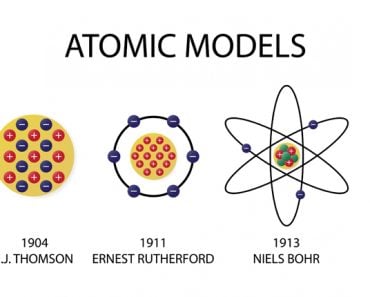
This was unexpected and quite contradictory, as light had previously been considered as a wave, which meant it had to be continuous. This also suggested that colors should be a continuous spectrum, and not quantized. Planck’s equation also contained a significant number, now widely known as Planck’s Constant. Quantization not only proved to be a pillar of QM, but also served as the substrate for other theories in physics. Einstein used Plank’s hypothesis of quantization to explain why the temperature of a solid changed by different amounts if you put the same amount of heat into a material, but changed the starting temperature. Niels Bohr also used it to disprove the planetary model of the atom and was able to triumphantly prove the theory of electrons moving in orbitals and requiring energy to jump from one orbital to another.
Particles Of Light
In 1905, Einstein wrote a revolutionary paper in which he envisioned light not as a wave, but as more of a continuous stream of energy packets known as quanta. Einstein hypothesized that the packet of energy could either be generated or absorbed whole, specifically, by an electron when it wants to jump from one state to another. With this new line of thought in terms of envisioning light, Einstein offered explanations of nine different phenomena, including the emission of varying light that Planck had brought about in the filament of the light bulb.
Using the particle nature of light, Einstein explained how electrons were able to eject from the surfaces of certain metals, which went on to become the photoelectric effect. It was due to this knowledge of the photoelectric effect that he was given the Nobel Prize in 1921. It was only after two decades, in 1923, that Einstein’s hypothesis confirmed by a scientist named Arthur Compton. He showed that the scattering of light by an electron beam resulted in the generation of colors. This went on to prove not only the particle nature of light in terms of quanta, but also the fact that even matter was of a particle nature. In today’s age, the dual nature of light—exhibiting both wave and particle-like qualities—is a widely known fact and has become the foundation of QM.
Waves Of Matter And Heisenberg’s Uncertainty Principle
It was only after the discovery of the electron in 1896 that the line of thought that matter could be of particle nature began. After the experimental proof that the nature of light is dual, being both a wave and a particle, scientists were even more inclined to move towards the notion that matter could also be dual. The first scientist who was able to make significant headway in this direction was Louis De Broglie. In 1924, de Broglie used Einstein’s theory of Special Relativity to prove that particles exhibited a wave-like nature and waves exhibited a particle-like nature.
Then, in 1925, two scientists working independently and using separate lines of mathematical thinking went on to explain how electrons whizzed around the atom. The movement of the electron that must be noted here was something that classical mechanics had hopelessly failed to explain. The German physicist Werner Heisenberg achieved the proof through a mathematical method called Matrix Mechanics. A second Austrian physicist, Erwin Schrodinger, developed a technique called wave mechanics. In 1926, Schrodinger proved that these two methods are equivalent, although certain scientists feel that Matrix Mechanics was more complete. The Heisenberg-Schrodinger model of the atom ended up replacing the Rutherford-Bohr model of the atom. The speculation of the new model was that electrons behaved more like a wave when they were closer to the nucleus. In this model of the atom, the electron follows a wave function property and occupies orbitals, not orbits. Unlike the circular orbits of the Rutherford-Bohr model, atomic orbitals have a variety of shapes, ranging from spheres to dumbbells and daisies.
Also in 1927, Heisenberg made another contribution to QM. He reasoned that since matter behaves as a wave, some properties, such as the electrons’ position and speed, is complementary to one another. To break that down into simpler terms, there is a limit up to which each property of the electron can be simultaneously measured with precision. This went on to be known as Heisenberg’s Uncertainty Principle. The more precisely you can observe the position of the electron, the less accurate one you can be in measuring its speed, and vice versa.
Bringing It All Together
The principle of quantization, wave-particle duality and the uncertainty principle ushered in the new era of QM. In 1927, Paul Dirac applied the quantum understanding of electric and magnetic waves to give rise to Quantum Field Theory (QFT). QFT treated all particles, such as photons and electrons, as excited states of the underlying physical world. However, work could not further progress because there was a roadblock in QFT; many results were pointing towards infinity, which did not make any quantifiable physical sense.
After a decade of stagnation, Hans Bethe made a breakthrough in 1947 using a technique called renormalization. Here, Bethe realized that all infinite results related to two phenomena (specifically “electron self-energy” and “vacuum polarization”), such that the observed values of electron mass and electron charge could be used to make all the infinities disappear. Since this breakthrough, QFT has been able to serve as the foundational explanation for electromagnetism, weak nuclear forces, strong nuclear force, and even gravity! The first insight provided by QFT was a quantum description of electromagnetism through “quantum electrodynamics” (QED), which made great strides in the late 1940s and early 1950s. Next came a quantum description of the weak nuclear force, which was unified with electromagnetism to build “electroweak theory” (EWT) in the 1960s. Finally, a quantum treatment of the strong nuclear force emerged using “quantum chromodynamics” (QCD) in the 1960s and 1970s. The theories of QED, EWT and QCD together form the basis of the Standard Model of particle physics. Unfortunately, QFT has yet to produce a quantum theory of gravity. That quest continues to this day in the popular studies of string theory and loop quantum gravity.
