Do We Have Any Mathematical Proof That Pi Is Infinite?

The proof for the infinite length of pi comes from mathematician Johann Lambert, who proved that pi is irrational, and therefore must be infinite.

The sixteenth letter of the Greek alphabet in mathematics holds as much significance in this universe as pepperoni in pizza holds for the average reader. From determining the size of your frisbee to calculating the expanse of our universe, this symbol has changed the world.

Any guesses on what it is?

π.

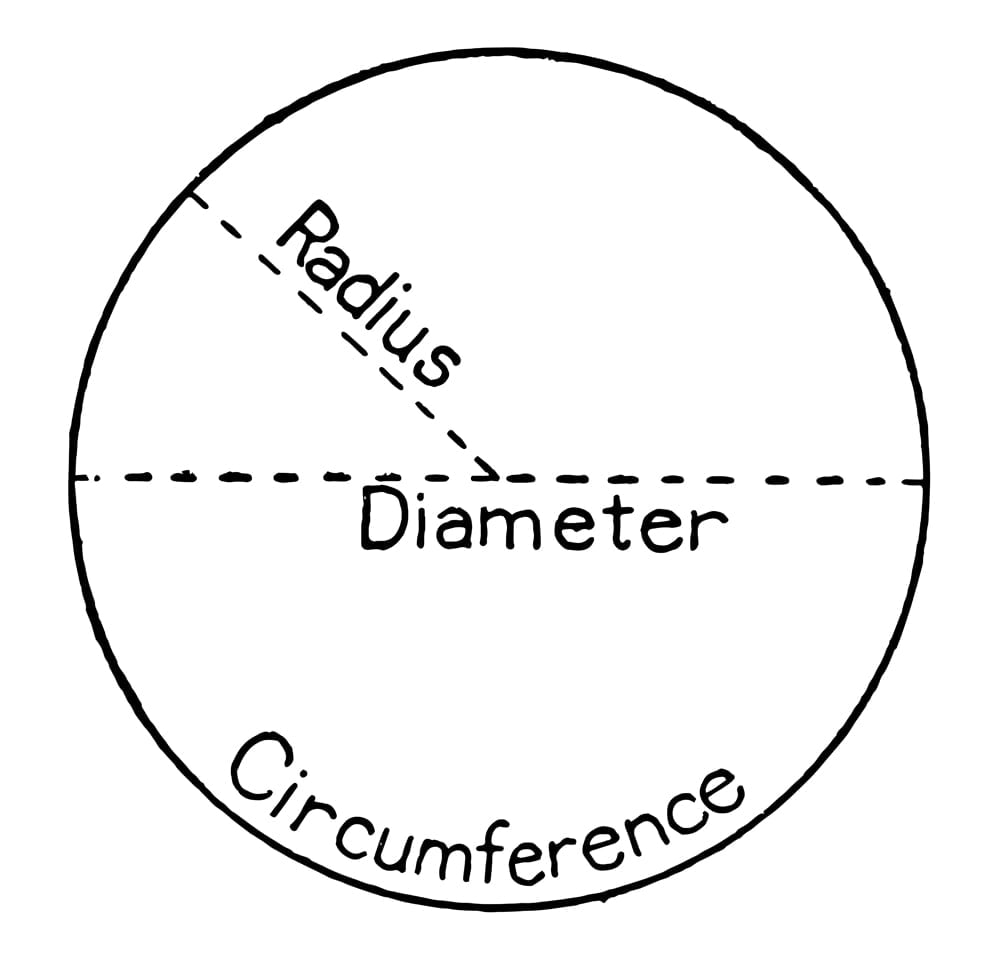
Two vertical lines flagged by one horizontal line: π (pi). You’ve probably heard or even used this symbol in your math class. The circumference of a circle is 2πr, where r is the radius of the circle.

Have you ever wondered about the origin of pi? And do we have any proof that pi is infinite? Moreover, is pi really what we think it is?

Recommended Video for you:

The Origin Of Pi

Our life has been dominated by circular objects from the very beginning. Wooden wheels back then, Hot Wheels today.

As a result of the universal function and presence of the circle, a common discovery that baffled ancient mathematicians all over the world, from India and Greece to Egypt and China. The diameter of a circle was always proportional to its circumference. No matter how large or small the circle was.

That is, the ratio of the circumference of a circle to its diameter always yielded a constant that was independent of the dimensions of the circle. Welsh mathematician William Jones was the first to call this proportionality constant pi because it represented the first letter in the Greek word for perimeter—perimitros. The name has stuck ever since.

No, Pi Isn’t 22/7 – Here’s Why

Many of use were taught that pi is twenty-two divided by seven in grade school. However, it is something more than that—and definitely not 22/7.

Pi is an irrational number.

So in essence, it cannot be expressed as the ratio of two integers that have no other common factor other than one. Then, why 22/7 you ask?

Well, this is actually just an approximation.

22/7 is 3.142; whereas pi is 3.1415—the value differs at only the third digit! The estimated value of pi used by NASA and for other scientific purposes contains around forty digits of pi!

Imagine if they made calculations with 22/7: Neil Armstrong and Buzz  Aldrin could have never reached the moon!

Is Pi Infinite? Why?

When mathematician Johann Lambert proved that pi is irrational, the fact that it is infinite came along at the same time. The reason for this is that all irrational numbers are infinite.

Pi belongs to a group of transcendental numbers. Meaning, it is not a root of any integer, i.e., it is not an algebraic number of any degree, which also makes it irrational. How? Because, a rational number is an algebraic number of degree one. Thus, if a number is transcendental, it is automatically irrational.

We just discussed that they can’t be expressed as a ratio of 2 numbers, which makes their decimal expansion endless. Their decimal expansion is non-terminating and non-recurring, i.e., the number never ends and never repeats. The reason for this is that if we have a finite decimal, 0.2378, for example, it can be represented as 2378/10000 or 1189/5000.

So, it can be expressed as a fraction, which makes it rational! So, for a number to be irrational, it cannot be expressed in a fraction and is thus infinite!

Don’t confuse the infinite expression of pi with its infinite value. Pi is finite, whereas its expression is infinite. Pi has a finite value between 3 and 4, precisely, more than 3.1, then 3.15 and so on.

3 < π < 4

Hence, pi is a real number, but since it is irrational, its decimal representation is endless, so we call it infinite.

How Do We Calculate Pi?

There are numerous ways of calculating pi. You can draw a circle, then measure its diameter using a ruler and its circumference using a piece of string. Now, divide the circumference of the circle by its diameter and there you have it—the value of pi! Voila!

The above method only gives us an approximate value of pi that is somewhere near 3. When I said that NASA only uses about 40 digits of pi, the simplest question that must have popped up in your head must be how did we come up with those 40 digits of pi?

Mathematicians all over the world have worked over the centuries to develop theorems and formulae that help us in calculating pi. The most respected methods for finding pi are:

1. Gregory- Leibniz
2. Newton
3. John Machin
4. Wallis
5. Ramanujan

The Gregory- Leibniz, Newton and Machin series are simpler to grasp and easier to comprehend, whereas the other means of calculating involve higher level of mathematics. A fun fact about pi

How Pi Is Related To ‘G’ – The Gravitational Constant

Take out your calculator and compute the square root of the acceleration due to gravity.

== ~

The square root of g is almost equal to the value of pi! Is that a coincidence?

There is an equation that typically depicts the relation between the time period and the length of a pendulum.

For an ideal pendulum of length one meter, the time period is 2 seconds. Boom! Using T=2 and L=1, we get,

π² = g

Pi is thus related to gravity!

The Life Of Pi

As you can see, pi is indeed an influential part of our lives! So influential, in fact, that it has a day of its own—pi day.

Celebrated on the 14th of March every year since its date stamp is 3.14, it also holds a position in the 5 super numbers of mathematics, which includes e, i, 0 and 1! Even the speed of computers is decided by how fast they can calculate the value of pi. Consequently, quantum computers can calculate about 2 quadrillion digits of pi!

The life of pi is as endless as its decimal expansion. The journey of pi has just begun and there are plenty of mysteries still to be unravelled!