Table of Contents (click to expand)
The proof is not as straightforward as it seems. While the idea behind it is not incorrect, the way it is presented is misleading. The proof hinges on the assumption that the sum of all positive integers 1+2+3+4…to infinity is equal to -1/12, which is not true.
What is 1+1? Pfft easy – it’s 2. What is 2+3? Well, slightly tougher, but doable, it’s 5. Next, what is 5+6? With no more fingers left to count on, a third hand would tell you it’s 11. All well and good. Now, what if I asked you to count infinite fingers tethered to infinite hands, or otherwise, the sum of all positive integers 1+2+3+4…to infinity? And what if I successfully proved that the answer, and you might want to sit down for this one… is -1/12?
How could the sum of whole numbers be a fraction? How could the sum of positive numbers be a negative number? The astounding and completely non-intuitive proof has been previously penned by elite mathematicians, such as Ramanujan.

The proof is often found in String Theory, an extremely wicked and esoteric mathematical theory, according to which the Universe exists in 26 dimensions. The theory is a promising contestant for being crowned as the Theory of Everything. So, it must be true… right?
Recommended Video for you:
The Proof
There are many ways to prove it, but let me refer to the simplest way I have come across. Consider first this sum S(1) of 1’s.
S(1) = 1-1+1-1+1-1+1…
The ellipses imply that the sum extends to infinity. The outcome of this sum depends on where we stop adding or subtracting the 1s. If we stop at an even 1, the sum crumples to zero, whereas, when we stop at an odd 1, the sum is equal to 1. This uncertainty is perturbing. We can get rid of it by simply taking the average of both extremes, which is ½.
Next, consider these two sums S(2) and S:
S(2) = 1-2+3-4+5-6…
S = 1+2+3+4+…
Now, add S(2) to itself, but with a slight twist. Add the other S(2) by shifting the numbers one place to their right.
2S(2) = 1-2+3-4…
+ 1-2+3-4…
This calculation would clearly result in the series 1-1+1-1+1… which is, if you are paying attention, S(1), whose value, as we’ve shown above, is ½. So, 2S(2) is 1/2 such that the value of S(2) is ¼.
Next, subtract S(2) from S, which gives:
1+2+3+4+… – (1-2+3-4+…) = 0+4+0+8+0+12+0+16…
Which can be also be written as 4 times (1+2+3+4…) or 4S. Now, we’ve got the hat, we just need to point and cast the spell.
We have shown that S-S(2) = 4S, but S(2) is equal to ¼. Which means -3S (exchanging S(2) and 4S) is equal to ¼. Simple multiplication puts the cherry on top and concludes that S = -1/12. Or, 1+2+3+4… = -1/12!
S-S(2) = 4S
∴ -3S = 1/4 (from S(2) = 1/4)
Or, S = -1/12
How Is This Possible?
The proof featured in a video published by the YouTube channel Numberphile ostentatiously titled as ASTOUNDING: 1+2+3+4+5+ … = -1/12. Physicist Edmund Copeland, the one proving it in the video, after accomplishing the feat, ecstatically admits that “it looks like mathematics hocus pocus”.
He adds, “intuitively you want to stop the sequence, but the minute you stop it…” he drops his hand, imitating a karate chop, gesturing that it wouldn’t work. Even summing the series to a googolplex (10 raised to the power 10, which is itself raised to the power 100) wouldn’t result in -1/12; it must be summed necessarily to infinity.
The startling proof illustrated in simplicity that verges on obviousness enabled the video to gather nearly 1.5 million views in the very first month it was published. However, it also caused an outrage amongst mathematicians, as its title is ostensible and the proof equally skewed.

The math deals with what is called an infinite series, a sum that goes on forever and ever. The sums can be grouped into three categories – convergent, oscillating and divergent. A convergent series is a sum that converges to a finite value, such as 1/1+1/2+1/4+1/8+… which converges to roughly 2. An oscillating series is a sum whose result vacillates between two values. This would be the very first series S(1) we encountered – 1-1+1-1+1-1…
And finally, a divergent series is a sum that progressively diverges to a larger, immeasurable value, namely infinity. The series 1+2+3+4+… is a divergent sum because it progressively becomes bigger and bigger until it reaches infinity. If this is so, or at least it logically seems to be, how did Ed Copeland manage to converge it, and even further… to a negative number, as if by some subtle magic?
Subtle magic is the appropriate term to define the video. It is an illusion where the essential details are quite cunningly swept under the rug. Consider the first series on which the proof seems to hinge — 1-1+1-1+1… The narrator here makes an expedient assumption that the value of this sum can be averaged to ½. Not entirely wrong, but grievously misleading.

Mathematicians like Euler deplored the uncertainty of oscillating and divergent sums. To get rid of which, they devised an argument that would somehow quantify them or ‘make’ them convergent. This witchcraft stems from a branch of complex mathematics known as analytic continuation. However, the method merely transmutes a divergent or oscillating sum into a sparsely different sum.
This means that we’re not summing the same sum anymore, but a sum that resembles the original sum very closely. Furthermore, the new sum isn’t equal to, say 1/2, in the usual sense of equal to, but it rather implies that the sum is assigned to or associated with the value ½. It is the value of the modified, weakly converging series that we assign to our diverging series. So, the assumption S(1) = ½ is not as trivial as I’ve made it appear above.

Similarly, every sum used in the proof is conveniently ‘converged’ with the help of this method, even the final sum – 1+2+3+4+… = -1/12. However, the method assumes a superior complexity when applied to it.
The Physics
But what about the proof’s use in String Theory that I mentioned in the prelude? The video zooms into a page in the two-volume textbook String Theory by Joseph Polchinski where the sum is cited as a formula. The proof is, in fact, used in physics problems, such as the Casimir Effect or when calculating the dimensionality of the Universe in Bosonic String Theory. Does its practicality make it viable?
Casimir Effect
The Casimir Effect is a phenomenon observed between two uncharged conductive plates. According to it, there exists an attractive force between these plates due to the presence of virtual particles bred by random quantum fluctuations. Problems such as these often entail divergent sums. In fact, the Casimir effect’s solution involves the very same sum 1+2+3+4+…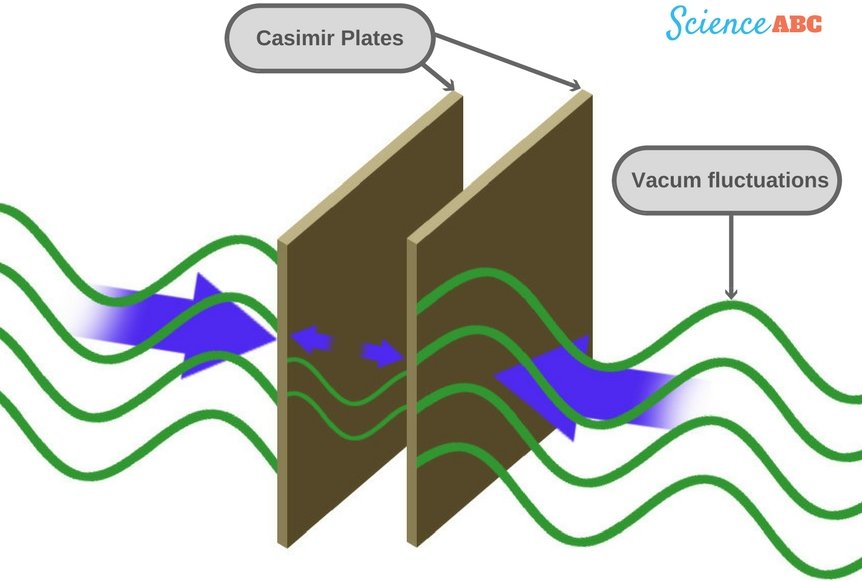
This would either imply that there is an infinite amount of energy seething between the plates, which is obviously nonsense. Or, there occurs a “dampening”, by which the energy becomes finite. The dampening or convergence is analogous to the convergence achieved by analytic continuation, expounded above.
Even the textbook does not explicitly use an equality sign, but rather an arrow that points the summation towards -1/12. The “dampening” is the acknowledgment of the fact that an unknown force is at work. Of course, the true sum of all natural numbers is not a negative fraction.













