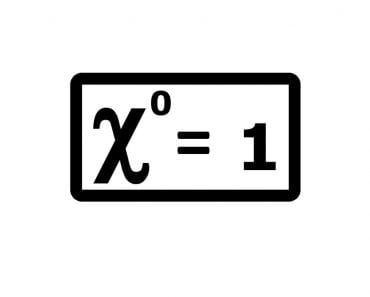Table of Contents (click to expand)
Dividing by zero is “undefined” or, to put it more impolitely, “nonsense” because it is contradictory or paradoxical. Mathematics is logical, like an intricate house of cards. The consistency of a structure relies on the consistency of the structure below it, which relies on the consistency of the structure below that. Essentially, the entire structure is built on the very first structure, let’s say, 1+1=2. Division by zero contradicts the most fundamental principle itself.
Veteran comedian Steven Wright once joked that black holes are where God divided by zero. Since mathematics arose several millennia ago, Man has disputed and reformed many conventions to keep his love affair with math alive. Centuries ago, the square root of negative numbers was believed to be non-existent until Gerolamo Cardano, in the 16th century, introduced the world to complex numbers, a branch of mathematics that entirely hinges on the square root of negative numbers.

However, there is one rule yet to broken, which is division by zero. And if dividing a number by zero is sacrilege, perhaps a cardinal sin, what is the result of zero divided by zero? If someone were to compute it, would the universe immediately begin to collapse in on itself? Let’s find out why the operation of dividing by zero is “undefined” or to put it more impolitely, “nonsense”.
Recommended Video for you:
Is It Really Equal To Infinity?
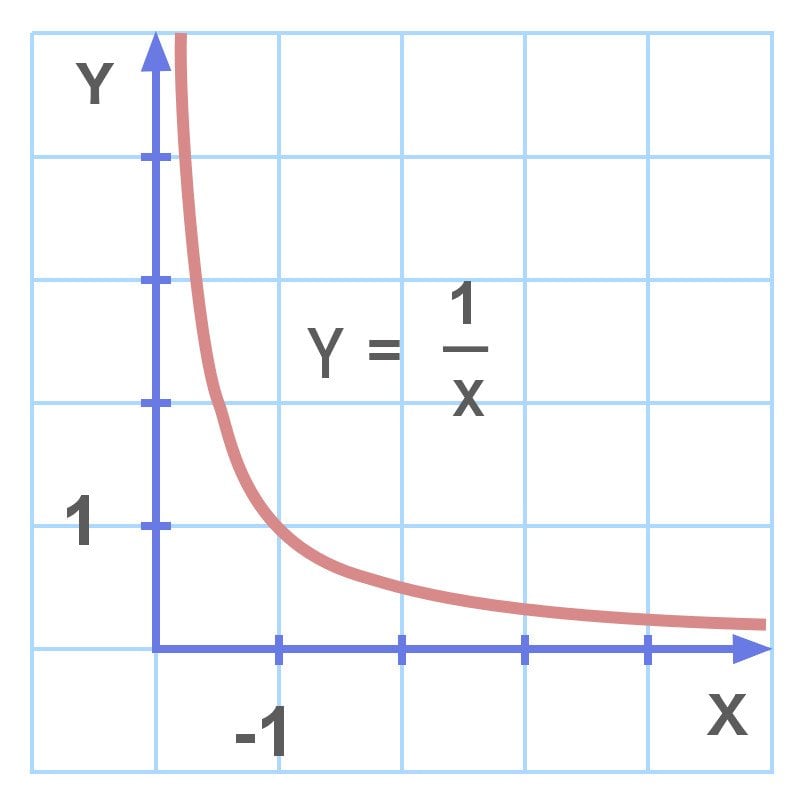
For convenience, a fraction in which the denominator is zero is often equated with infinity. This argument has some merit, considering the nature of the inverse function. You have likely observed that dividing a number by smaller and smaller numbers produces larger and larger numbers. For instance, consider these fractions:





As the numbers get infinitesimally smaller, the trend can be traced toward infinity. However, tending to infinity and being equal to infinity are two very different notions. The result seems to be on its way to infinity, but it never arrives.
Infinity is not a rigid number, but rather an idea; it only exists in abstraction. However, if we were to treat infinity like a distinct number and equate it with the fraction 1/0, we’d encounter absurd mathematical anomalies, particularly the most fallacious of all the maxims in mathematics:

for 

One can determine why this fraction is meaningless by referring to the definition of division. The most basic definition of division is, of course, to break something into parts of a certain size. For instance, when we divide 20 by two, the result is two parts of size 10 each. What then does it mean to divide 20 by zero? The result is no longer parts of a finite size. It would have been finite and very large, even when we divide it by 0.000000000000001, but the moment we divide it by zero, the logic of division is no longer preserved, and the result is unclear.
Another way to define division is as glorified subtraction. The outcome of 100 divided by 10 is the number of times we can subtract 10 from 100 until the result is 0. The result, I would hope you know, is 10. However, again, dividing 100 by 0 seems to be infinite, as the subtraction goes on forever.
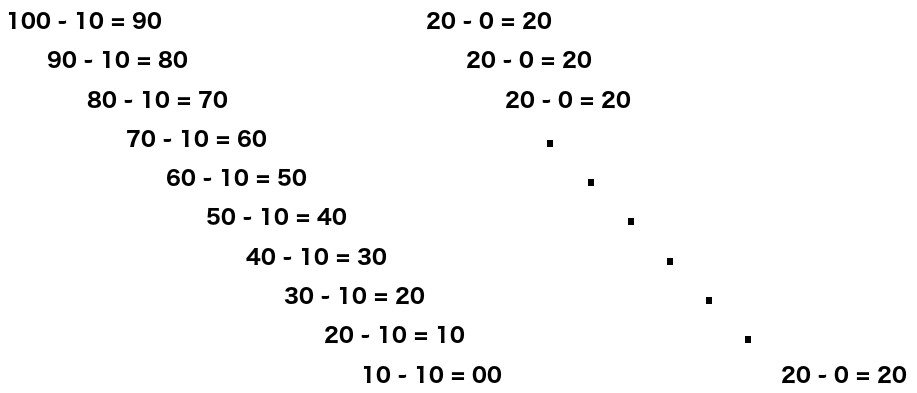
Is the result therefore infinity? Not really. As mentioned earlier, the logic of the operation isn’t consistent with our axioms. To verify whether 100 divided by 10 is really 10, we can add 10 ten times to check if the sum really is 100, which it is. We simply add the number being subtracted the number of times we obtained from the division. Therefore, to verify whether 100 divided by 0 is infinity, we must add zero infinite times. However, how could the sum 0+0+0+… possibly be equal to 100?
This brings us to our second question.
What Is 0/0?
Let’s assume that the result isn’t infinity, but rather a finite value, which we will denote with ‘x’. The operation then implies that x multiplied by 0 is 100, which is just as ridiculous as the contradictions we obtained in the previous section.

What’s not contradictory and illogical is the statement that anything multiplied by zero is zero. Thus, the equation then assumes the following form:

This can be reconfigured and written as:

Notice how this is true for any value of x. It doesn’t matter if x is a whole number, rational number, integer or complex number. This is atrocious, considering that for it to be true, not only must one equal two, but one must also equal every other number that exists! The infinite contradictions cause the entire number system to break down and the universe will immediately begin to collapse in on itself!
While it’s physically impossible to achieve this, mathematicians instead say that the division is “undefined” because it is contradictory or paradoxical. Mathematics is logical, like an intricate house of cards. The consistency of a structure relies on the consistency of the structure below it, which relies on the consistency of the structure below that. Essentially, the entire structure is built on the very first structure, let’s say, 1+1=2. Division by zero contradicts the most fundamental principle itself.