Table of Contents (click to expand)
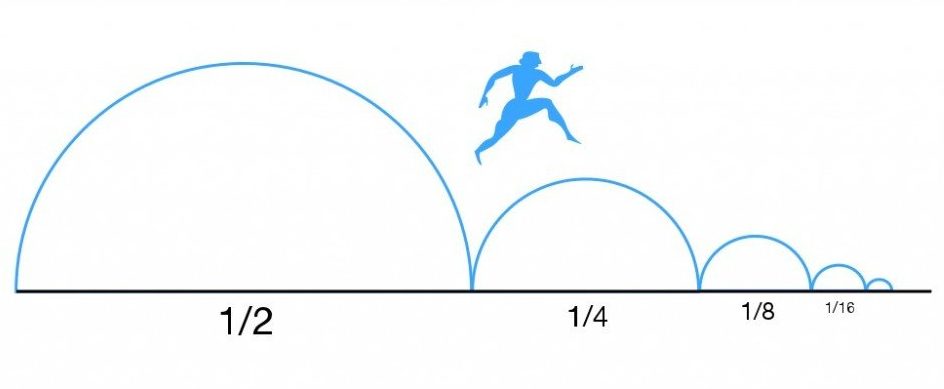
Zeno’s Dichotomy Paradox is the philosophical argument that states that an infinite number of things cannot be performed in a finite amount of time. The paradox is based on the idea that if you are in the middle of a room and want to get to the door, you must first walk halfway to the door, then halfway from the point where you previously stopped. You need to keep repeating this until you reach the door, but you will never actually reach the door because with each motion, you only cover half the distance of the previous steps.
Suppose, says the ancient philosopher Zeno of Elea, that you are in the middle of a room and want to get out. The door is open and nothing is blocking your path. Go ahead and walk to the door—except there is a tiny problem. To get there, you must walk halfway to the door, then halfway from the point where you previously stopped. You need to keep repeating this until you reach the door. Sounds pretty simple, right? How long do you think it would take before you reach the door? Better yet, do you think you would reach the door in your lifetime?
Recommended Video for you:
Implications
Now, as straightforward as that seems, the answer to the above question is that you will never end up reaching the door. To top it all off, even if you do try an infinite number of times (infinity isn’t a number, but for the sake of argument), you still wouldn’t be able to reach the door. The plain answer to the question is that with each motion, you do get closer to the door, but your succeeding steps will only cover half the distance of the previous steps. The steps you take consequently never really close the gap. There’s also another neat piece of parlor logic that can be applied here, apart from the step method. When it comes to respect to time, an infinite number of things cannot be performed in a finite amount of time, so the person cannot leave the room.

Zeno’s argument, at a cursory glance, might seem very silly, but this argument (and three others) worked together to criticize some of the most respected and ancient ideas about space, time and motion. However, more than a philosophical standpoint, we will also consider the mathematical implications. What Zeno noticed was that a given distance seems to be equal to the sum of all those halves. In modern terms, Zeno stumbled upon what is known as a limit, which became a fundamental tool in physics and mathematics from the 18th century onwards.
Where It Matters
Infinites bother people, and not just from a philosophical standpoint. The fact that you can add up something seamlessly infinite and end up with something perfectly quantifiable seems a bit dodgy from the onset. Basically, if one were to add up to infinity, it would be a failure, as we would not be able to complete the task. However, another revered philosopher comes to the rescue in this situation, none other than Aristotle. Aristotle goes on to say that not all infinites are the same. Some are actual infinites, while others are known as merely potential ones, which can go on as long as you like without any definite end-point. The easiest analogy for this is counting. A person can count as high as they want, but as soon as one feels that they have reached the highest number they possibly can reach, you can always add a one to it and make it bigger. That makes counting a potential infinity. What happens in Zeno’s paradox is similar to counting.
This became a major problem when physics started using new mathematical concepts, such as calculus. These methods seemed to provide practical feasibility, but they relied on infinitesimal distances that the scientists of the time could not justify. What if Newton’s greatest mathematical brainchild was just as absurd as Zeno’s paradox? Thus, a lot of bright minds jumped onto this bandwagon to try and get to the bottom of these lurking infinity issues. This is where the idea of the limit was born.
Understanding The Depths
Before we get into understanding limits and fully unpack Zeno’s Dichotomy, we will have to understand two standard notations, both of which Zeno himself could not have wrapped his head around, given his ancient knowledge base. The first is the zig-zag E, which is popularly known as sigma (∑). This is the capital letter for sigma in Greek. The second notation is the term lim itself. Sigma is the Greek alphabet’s equivalent to the English S. Here, S stands for the sum. Although the term sum can be thrown around in mathematics for quite a few things, here it refers to ‘counting up’.
At the bottom of the sigma is the little equation, ‘i=1’, and on top of it is ‘n’. These are primary clues in place that give us important parameters about the equation at hand. Imagine, in this instance, that sigma is a building with n stories. We go in on the ground floor, which is ‘i=1’ and start hiking up the stairs. Each time we reach a new landing, we add 1 to ‘i‘ and then find the value of the thing after the sigma sign. We make a note of that result and move on to the next floor. When we reach the top ‘i=n’, we add up all the values we have accumulated so far and take that as the final result. Now, if we apply this to Zeno’s Dichotomy and say that the person takes ten steps, then the person is this much closer to the door:
![]()
Let’s take a moment to understand how this sum makes sense. First, it is half the distance, and then a quarter of the original and then one-eighth, progressively becoming smaller. Adding all of these will give us a number that tells us we are very close to the door, but not quite there yet. However, there’s a nice catch here if you observe closely. We set the limit as ten steps, not like in Zeno’s original paradox. He says that no matter how many we take, we will get closer and closer, but never quite reach the exit. This is where the term “limit” comes into the picture.
![]()
Take a look at the equation above. As n gets bigger, 1/n gets smaller and smaller. It gets extremely close to 0 when n is very big.
What’s more, if you give any ‘margin of error’, however small, you can always find the value of n so that 1/n is closer to 0 than your margin of error. From that point onwards, as n increases, 1/n always stays within the margin of error. It is famously said that n tends to infinity, and 1/n tends to 0. In conclusion, we can say that approaching a limit by an infinite number of smaller and smaller steps sounds like philosophical wordplay, but it lies at the heart of calculus as one of the most useful mathematical inventions of all time.













