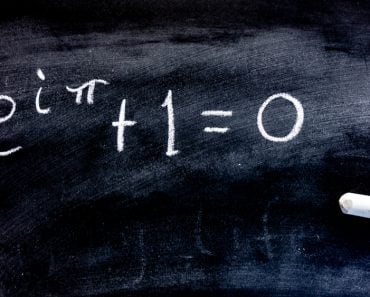Zero Power Rule: Why Is A Number Raised To Power Zero Equal To One?

The number one is raised to the power of zero because it is the multiplicative identity. The number one is raised to any power and it will still equal one.

Seriously? This was definitely taught in high school, but as well all know, most of what was taught in high school now seems redundant. I mean, do you remember having to recall that mitochondria are the powerhouse of the cell while doing your taxes? Yep, me neither.

Nonetheless, this article poses a tantalizing query! These queries illustrate that we mentally photographed and framed certain mathematical expressions ages ago, but have now forgotten all the events that led up to this picture. These expressions have become crucial tenets – principles that we blindly accept without any skepticism. Their proofs have long eluded us.

Let me remind you that the rule — a number raised to the power zero is one — isn’t arbitrary or a convention; nothing is arbitrary in math. This is, in fact, true for many such basic, yet perplexing queries, including why the factorial of zero is one.

These are highly basic or primary problems, as they are deeply rooted in the constitution of their corresponding disciplines itself. Thus, they require thorough conceptual knowledge, which most of us lack, probably because we never effectively put it to use.

First, let’s go back to the basics.

Recommended Video for you:

The Exponential Function

An exponential function is a function that assumes the form xª, where x represents a constant, known as the base, and ‘a’, the power of this function, can be any number. Initially, the constants were only raised to positive numbers. However, the function’s domain expanded and the number to which the constant could be raised extended to a fraction, negative, a negative fraction or even a complex number!

The function represents a large self-multiplication operation of a number that is multiplied by itself, hitched onto whose shoulders is the power number, or the number of times the number self-multiplies. For instance, 3³ represents the operation 3x3x3, which is 27. However, consider (81)½. Its outcome is a number that, when raised to the power 2, gives us 81 (9, if you didn’t know). Simply, a fractional power represents a root of the base number.

Furthermore, negative powers represent the reciprocal of the exponential function, such that now the function is the exponential function with the positive power divided by one. For instance, 3^-2 implies (1/3)². Another principle that is imperative to remember is when two exponential functions with the same base are multiplied to each other, the outcome is the base raised to the sum of both powers. For instance, (3×3) x (3) is 27 or 3³ or 3²⁺¹.

Another way of looking at the exponential function is in terms of combinations. 2³ represents all the sets of three numbers where each number is either of two numbers, let’s say 1 and 0. The two numbers can be combined in 8 ways – (000), (001), (010), (011), (100), (101), (110), (111) giving 2³ as 8.

So, what does 2º represent?

Why Is Any Number To The Power Of Zero Equal To 1?

Considering the myriad ways in which the exponential function can be defined, one can solve for xº by referring to every single definition, which is really the fairest way to go about it.

First, let’s refer to the combinational definition. To get a more palpable idea replace the numbers with physical objects. How do we arrange a pen and a pencil in sets that contain none of them? Only one, by not placing them at all!

Well, I’ll admit that this sounds extremely fishy. So, instead, we’ll refer to the next principle. Consider this pattern:

Pattern 1 :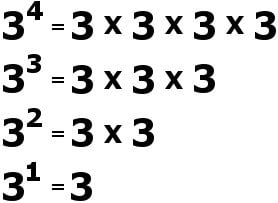

The pattern can also be extended to negative numbers, giving:

Pattern 2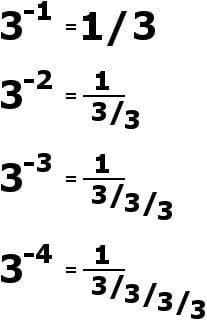

To summarize, we can write x^a-1  is equal to x^a /x (this reduction doesn’t even need a long pattern; we can arrive at it by cleverly tampering with the multiplication principle itself). Now, when a is 1, the value of xº becomes x¹/x, which is 1.

However, in my opinion, the most instructive proof would be the multiplication approach. If we multiply xª with x^-b, the outcome according to the multiplicative rule would be x^a+(-b) or x^a-b. Now if the numbers a and b are equal, the outcome would be xº.

Now, because x^-b can be written as 1/x^b, the above multiplication can be written as xª divided by x^b. And if a and b are equal, then the two numbers are equal, giving us xº = 1! For instance, 3³ multiplied by 3^-3 is  3³ x 1/ 3³, giving 3º=1.

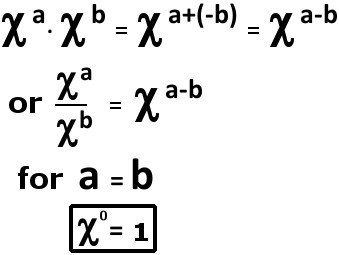
Hence, proved!