What Is Euler’s Number?

Euler’s Number is an irrational mathematical constant represented by the letter ‘e’ that forms the base of all natural logarithms

The mathematical constant ‘e’, popularly known as Euler’s number, is arguably the most important number in modern mathematics. I’m not exaggerating when I say that Euler’s number has touched each and every one of our lives in some way at some point in time.  From trigonometry to compound interest calculations, it appears everywhere!

Recommended Video for you:

What Is Euler’s Number?

Numerically, e = 2.7182818284…

More specifically, it is a number with infinite digits beyond the decimal point; it follows no discernible pattern and cannot be represented as a definite fraction. Essentially an irrational number, it forms the base natural logarithms, i.e., ‘ln’. The number facilitates the forecasting of numerous growth rates, from the growth of financial indices to the rate of the spread of diseases. Any growth in a financial index or the growth of a disease-spreading virus would eventually follow a pattern governed by ‘e’. Let’s look at a simple example to better understand how this constant comes about.

Imagine that your investment-savvy friend asks for $100 and claims that he can double it in a year. At the end of the year, he’ll give you $200, guaranteeing you a 100% return on investment. If that’s true, if you ask for your investment back in 6 months, theoretically, he should give you a return of 50%, which would total $150. If you take the $150 at the end of 6 months and put it back in his “fund” for the remaining 6 months, at the end of the year, you would receive $225. That’s an extra $25.

Now, what if you took your money out each month and re-invested it? You would be making about $271. And what if you took your money out at the end of each day? You would make approximately $271.82… See where this is going? Instead of doubling your money, you’ve managed to grow it exponentially. In other words, you’ve made your money grow by a factor of ‘e’.

Evidently, e is the result of:

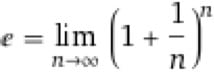
As ‘n’ grows larger, the resultant value approaches Euler’s number.

This is all too familiar for high school students learning about compound interest. If your principal is set to double at the end of the year, but you continue to reinvest the daily interest accrued, thus compounding your interest, your principal will eventually end up growing by a factor roughly equal to ‘e’

This interesting mathematical constant has an equally interesting origin story.

Also Read: Euler’s Identity: ‘The Most Beautiful Theorem In Mathematics’

The Origin Of Euler’s Number

Euler’s number first appeared when John Napier, a 16th century mathematician, was looking for a way to simplify the process of multiplication. He devised a process called dynamic analogy, through which multiplication would be converted to addition; concurrently, division became simple subtraction. He created two columns where the product of two numbers in one column was analogous to the sum of two numbers in the second column. In fact, this was a preliminary version of today’s natural logarithmic tables. Throughout his process, Napier never actually acknowledged the presence of ‘e’, but was using it without explicit realization. Today, it’s common knowledge that ‘e’ forms the base of every natural logarithm.

Over a century later, Euler’s number was explicitly identified. Gottfried Leibniz, a competitor of Sir Isaac Newton, discovered the constant during his work on calculus. Its first mention was recorded in a letter that Leibniz wrote to Christian Goldbach, in which he named the constant ‘b’. However, it was much later, around the 18^th century, when Leonhard Euler gave the mathematical constant its modern designation ‘e’ and detailed several of its astonishing properties. Oddly enough, ‘e’ does not stand for Euler’s name, but is instead a result of his love for vowels. When Leonhard found that ‘a’ had already been taken, he couldn’t wait to jump at the next one and eagerly picked ‘e’ to represent his special discovery.

However, it’s surprising that a mathematical constant that had such a significant impact on modern mathematics was discovered at such a late stage in human civilization. In contrast, the constant (22/7) that we all affectionately call Pi was first discovered sometime around 550 BC!

So we have a basic idea about what ‘e’ means and where it came from, but what’s the big deal? Why is this constant supposed to revolutionize modern mathematics?

Also Read: What Makes Natural Logarithms “Natural”?

Euler’s Identity: Properties Of Euler’s Number

Euler’s number has several interesting properties that crosses the spectrum of mathematical topics. The differential of e^x is e^x. Its integral is simply e^x + C (constant). If you took a differential of the natural logarithm of e^x (ln e^x) you would arrive at 1/x.

In trigonometry, ‘e’ also helps to derive an interesting result:

e^ix = cos x + i sin x.

This manages to establish a relationship between two trigonometrical functions (sin and cos) and i (√-1), which is quite the feat! Moreover, if you assume that the value of x = π, the formula gives rise to yet another interesting relationship.

e^iπ = cos π + i sin π

cos π = -1 and sin π = 0

Consequently, we arrive at an elegant and powerful result combining three of the most interesting variables in mathematics: ‘e’, ‘i’ and ‘π’.

e^iπ = -1

This is more commonly written as:

e^iπ + 1 = 0

This is popularly known as ‘Euler’s Identity’.

These identities and properties provide a useful tool for those dealing with complex analysis, such as money managers on Wall Street, computer programmers designing the next revolutionary app, or scientists at NASA planning the next mission to Mars. The implications of Euler’s number are clearly far-reaching!

While this article certainly doesn’t represent an exhaustive list of the properties and features of Euler’s number, it is a great starting point to pique your interest. Those hungry for more in-depth information can now pop over to an academic article about Euler’s number and you won’t be entirely clueless about what’s being discussed!