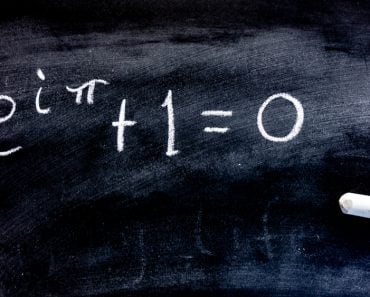An imaginary number raised to an imaginary number turns out to be real. However, while learning complex analysis, one learns that an exponential with respect to an imaginary number does not have a single, fixed value. Rather, the function is multi-valued — the value we arrived at in our calculation is just one of many values.
The imaginary unit 
represents the square root of -1, such that 
. Imaginary numbers live in a world of their own; the numbers are counted on an entirely different plane or axis that is solely devised for them. However, imaginary numbers have acquired a somewhat nefarious reputation, considering that their discovery has compounded the difficulty of problems that math was already replete with. I mean, as if the numbers we already had weren’t enough?
Our problem, however, combines not just one, but two of the many haunting aspects of mathematics. If itself is so difficult to comprehend, what could 
be? You might be surprised to know that unlike , the value of is a real number! How is that possible?
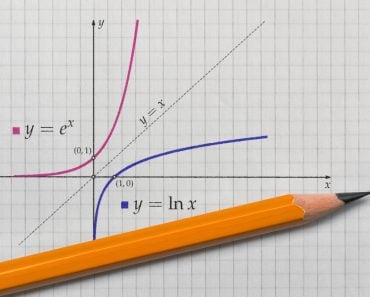
First, we must revise one of the most common, but least understood, mathematical operations — logarithms. Let me remind you how they work: If 
, then 
. For instance, given that 
, 
. Here, b is called the base of the logarithmic operation.
To solve the problem at hand, the base of our operation is 
, or Euler’s number, with a value of 2.71828… If 
, then 
. The logarithm with the base is known as a “natural logarithm”. It is imperative to understand that the exponential and logarithmic functions are inverse functions. This is very important for our calculation.
The second thing to recall is that can be written as a complex number 
, which can also be written as 
. However, according to Euler’s formula, 
. Therefore, 
is equal to 
.
Now, let’s say 
. Applying logarithm on both sides of the equation, we get:
Remember that logarithmic and exponential functions are inverse functions, such that 
. Thus, from the above expression, one can discern:
Applying the exponential on both sides of the equation:
Again, we encounter the inverse functions together. They neutralize to give the outcome:
Thus, an imaginary number raised to an imaginary number turns out to be real. However, while learning complex analysis, one learns that an exponential with respect to does not have a single, fixed value. Rather, the function is multi-valued — the value we arrived at in our calculation is just one of many values. This is because the value of isn’t particularly , but 
, 
and every odd multiple of 
. Therefore, the value of also varies from 
to 
, 
and so on.
Recommended Video for you:
