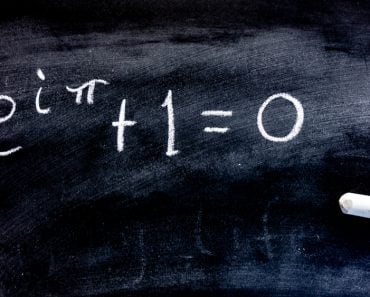Table of Contents (click to expand)
Pi is so important because it is a transcendental, irrational number – the digits occurring after the decimal point are inexhaustible. They go on forever and ever. The number of digits is currently known to surpass 2 trillion! This implies that the number 3.14 or even 3.145926 is an outrageous approximation.
It is everywhere. It is in the blinding disk drawn by the Sun and on both sides of my unlit cigarette. It is in the outline of capacious domes worn like skull caps by sanctimonious cathedrals. It is in the letter ‘O’ painted so cautiously on my keyboard and the physiognomy of the number ‘9’ just above it. It is at the blunt end of a pin and in the heart of magnificent sunflowers. π truly is everywhere.
I was first introduced to π in middle school, in what seemed to be an interminable chapter called Measurements. The long chapter illuminated the many ways we can gauge aesthetics – the perimeter of a rectangle, the area of a circle and the volume of spheres. I had never looked at these whimsical shapes so analytically before. All the shapes harboring a curve were described with the help of a constant that appeared to be a miniature pair of diverging swings hanging from an extended metal bar – π. The chapter claimed its value was equal to the ratio 22/7.
The indulgent authors of the textbook tested us with problems involving a calculation where an adroit trade of symbols across the equal-to sign would ensure that the ratio is canceled, and the calculation loses its complexity. Back then, multiplications had to be performed manually, without the help of calculators. Impatient kids would use the value 3.14 — the quotient of the division 22/7 — and become trapped in the web of arduous decimalized calculations.
Circles are some of the most ubiquitous shapes in the Universe. However, their nonlinear shape makes studying them quite difficult. Even something as trivial as finding the area of a circle is a challenge. One thing is obvious – the circumference or area of a circle is directly proportional to its diameter; as the ring expands, logically, so does the area it covers. The two can therefore only be linked with a constant — the ratio of the two proportional quantities, namely diameter and circumference. Because the ratio is so intimately linked to circumference, the Greeks called it π, which is Greek for ‘p’, the starting letter of the word periphery.
Recommended Video for you:
The Circle’s Absurdity
The absurdity fostered by something as innocuous as a circle compelled the Greeks to determine this constant. One way to do this is tightly packaging the circle in another shape and measuring the area of this package. They circumscribed the circle with straight-edged polygons. The difference between the area of this polygon and the negative space left between the two would give us the area of the circle and therefore, the value of this constant. Consider the simplest polygon — a square — that can be used to demonstrate this.
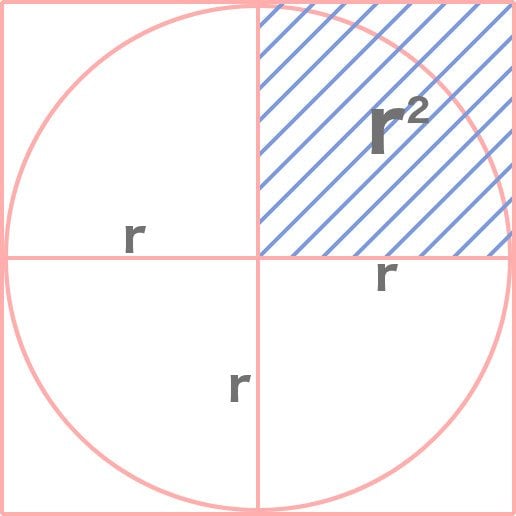
This is nothing but a pizza in a square box. Now, the area of one square is 
, such that the area of the entire square is 
. However, discounting the negative space, it is clear that the area of the inscribed circle must be less than . This gives us an upper limit to the value of π. What’s more, the area is surely greater than 
, which also gives us the lower limit. Thus, we have realized that the value of π lies between 3 and 4. Babylonians believed that the area of a circle is three times the square of its radius, which implied that the value of π is 3. A few Babylonian texts, however, inferred π to a more precise value of 3.125.
In the above example, a more fitting polygon would enable us to calculate it with superior precision. This is exactly what Archimedes, arguably one of the greatest scientific and inquisitive minds of antiquity, did. He devised a way that allowed him to calculate π’s value to any degree. Archimedes initially inscribed and circumscribed not squares, but hexagons, in and around the circle. Then he doubled their sides until the polygons approximated it almost perfectly. This continued until he drew a highly detailed 96-sided polygon that would fit the curved line like an envelope. Archimedes arrived at a window for this constant between 3 10/71 and 3 1/7.
In fact, Archimedes was so engrossed with his diagrams that when a Roman soldier tried to arrest him while the city was under siege, he reportedly berated the soldier and asked him not to “disturb my circles”. Hearing this, the soldier grew incensed and decapitated him with his sword. Due to his unflinching diligence, the ratio is also known as the Archimedes constant.
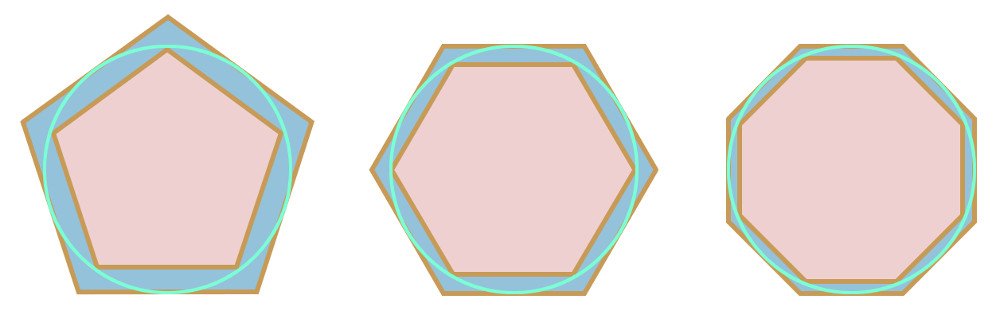
Later, in the 5th century A.D, Chinese mathematicians further squeezed the walls on π — they found that it lay somewhere between 3.1415926 and 3.1415927, an unprecedented accuracy that Europe wouldn’t attain until the 16th century. Due to its tediousness, the polygon technique grew outdated and defunct, but it left us with a profound dilemma — is a circle corner-less or composed of infinite corners?
The vestigial method was replaced by the proficient tools of modern math. Euler used the infinite series method to discover a few more buried values. His raging popularity in Europe drove other mathematicians to denote the ratio by the anachronistic symbol ‘π’, a symbol he used “for the purpose of brevity”. Subsequently, Newton used the binomial theorem to calculate the value of π to 16 digits after the decimal point.
Approximation And Uncertainty
Back to middle school, where my misery worsened when I realized that all my toiling was futile. The chapter ended with a grim conclusion. Pi, as we learned, is a transcendental, irrational number – the digits occurring after the decimal point are inexhaustible. They go on forever and ever. The number of digits is currently known to surpass 2 trillion! This implies that the number 3.14 or even 3.145926 is an outrageous approximation, which therefore implied that the areas of different shapes I so drudgingly calculated were inevitably erroneous.
In fact, if we were to calculate the areas with a value of π extended to the number of seconds in 4,000 years, the entirety of time since we discovered π, we’d still be approximating! Because our investigations are not based on π’s true value, but rather an approximation, our predictions are also bound to be approximations. The discoverer of this characteristic proved that the square root of π is also transcendental — the number cannot be the root of a non-zero polynomial equation with integer coefficients. This profound finding finally settled a perennial problem in geometry that asked – how must one “square a circle?”
The “squaring a circle” is an age-old challenge to construct a square with the same area as a circle using finite steps and a straightedge. The latter is impossible to accomplish since the side of this square turns out to be the square root of π, which we have learned is an interminable trail of numbers. The straightedge can be divided into only so many units; the moment we stop dividing, we commit the grievous fallacy. Convenience comes at the cost of precision; the resulting square, like the area of the circle in my textbook, is then merely an approximation, not the same circle.
Furthermore, the trillion digits fall into no pattern whatsoever – their distribution is truly random. This is particularly infuriating for humans, who are essentially pattern-seeking creatures. To my despair, π’s tentacles weren’t constrained to mathematical ventures… they also sidled into cultural avenues. I made π’s acquaintance again while reading Carl Sagan’s science fiction novel Contact, which depicted that the creator of the Universe buried a secret message within the digits of π.
Such stories spark fascination that often verges on sanctity. How could the mere ratio of a circle’s circumference and its diameter conceal such profound significance, such varied and dense complexity that left even Newton nonplussed? The fascination fuels speculation, which eventually found that the digits appear non-random at one point, where a sequence of six consecutive 9’s emerges. They begin at the 762nd decimal place, a position famously nicknamed the Feynman point, after the genius physicist Richard Feynman.
Of Computers, Prodigies And Misfortune
Finally, the advent of computers enabled automatic calculation of π’s trailing digits. John von Neumann’s ENIAC took a prolonged period of 70 hours to calculate π to 2,037 digits. Subsequently, better processors accrued more precision – 7,450 in 1957, 10,000 in 1958 and 1 million in 1973. Now, superlative computers have surpassed the trillion-digit mark. One site is solely dedicated to enumerating the initial 100,000 digits. However, why do we vehemently churn these numbers when calculating the circumference of the observable Universe to the accuracy of an atom requires the value of π to only 40 digits? Is it to satiate something transcendental like wonder or curiosity? Or is it something smug like seeking praise for breaking a record?
The latter might be the answer to why people participate in piphilology, the learning of mnemonic techniques to try to remember the seemingly infinite number of digits. The current record is held by Rajeev Meena who recited 70,000 digits in 9 hours and 27 minutes! Computer scientists actually calculate π as a benchmark test for computers. The extensive multiplications test a computer’s processing speed and encourage the development of efficient algorithms to facilitate the exacting process. In fact, in an episode of Star Trek, an evil supercomputer is ingeniously halted after it is asked to calculate the value of π. That’s genius!
Yet such a demanding computation did not agitate everyone. While the ordeals of my middle-school math classes traumatized me, math prodigy Zacharias Dase reveled in calculating the value of π to 200 digits in his head. However, there existed someone who was even more unfortunate than me – British mathematician William Shanks, who spent almost 15 years calculating π to 707 digits, but a tiny mistake, a miscalculation while computing the 528th digit, rendered the subsequent numbers incorrect!
Life Of Pi
Due to its affiliation with circles and curves, it is found in a myriad of fields that pertain to curvature or rotation. In fact, π is so deeply linked with circles that at the 359th place following the decimal, you will find the number 360! Pi is also used to derive Euler’s Identity, what is acclaimed to be the ‘the most beautiful theorem in mathematics’. It is found squeezed between constants and numbers larger than it in the equations of General Relativity, the modern theory of gravity that governs the movement of the cosmos. It is even found in Quantum Mechanics, the realm of atomic and subatomic particles where probability reigns supreme (see Heisenberg’s uncertainty principle).
However, it is also found in places one would seldom expect. It is prevalent in numerical statistics, number theory, conspiracy theories (the first 144 digits add up to 666, the number of El Diablo) and on the walls of a circular room called the Pi room in the Palais de la Decouverte, a beautiful science museum in Paris. The walls are transcribed with the corrected version of the 707 digits so laboriously computed by Shanks.
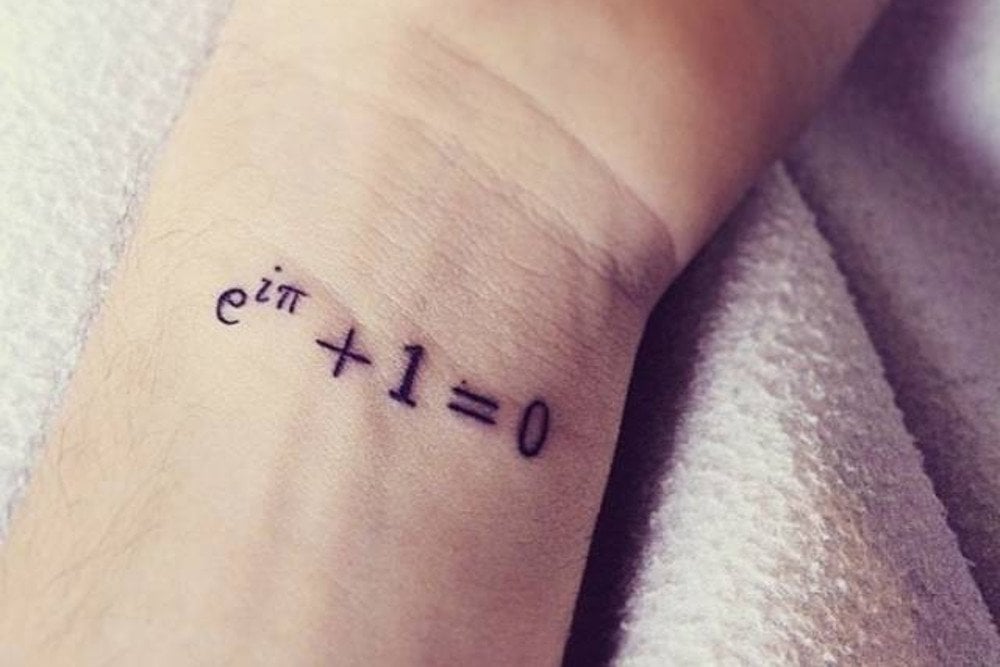
During Nortel’s auction of valuable technological patents in 2011, Google made a series of peculiarly particular bids that were later identified to be mathematical and scientific constants, such as the distance between the Sun and Earth. When the bid reached $3 billion, Google retorted with $3.14159 billion, which was, of course, a reference to π. One source wanly commented, “Either they were supremely confident or they were bored.” Their shenanigans, however, were ineffectual, as all bids were turned down.
The captivating mystery of pi has earned it the honor of being the most identifiable mathematical constant amongst the pantheon, which includes Euler’s e. Its overwhelming popularity has coerced the U.S. House of Representatives to declare March 14th as Pi Day to encourage students and teachers to spread awareness and celebrate its importance. The celebrations commence at 1:59. The anniversary was even more significant in 2015 when the date and time lined up so ceremoniously as 3/14/15 at 9:26:53 (you might want to read the article again if you don’t get these references).
Even the food industry couldn’t shy away from the celebration — cafes and dessert parlors in a range of cities are looking forward to selling ‘Pies on Pi day’ at a beguiling price of, exactly what you guessed — $3.14. Don’t forget to share the pie, and the article. Happy Pi Day!
