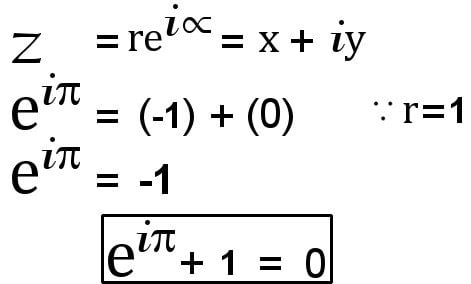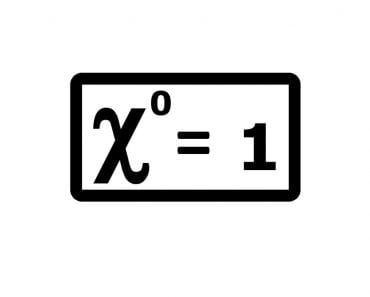Table of Contents (click to expand)
Euler’s identity is held to be the “gold standard of mathematical beauty” because it links seemingly different branches of mathematics in an exquisitely simple manner. The expression possesses Euler’s number ‘e’, the base of natural logarithms that is extensively recruited in calculus. It also possesses ‘i’, the complex or imaginary unit, which is the square root of -1.
Leonhard Euler was an 18th-century Swiss-born physicist who developed numerous concepts that are indispensable to modern mathematics. A highly prolific mathematician, Euler is considered to be one of the greatest of all time for his inestimable contributions.
Throughout his life, Euler published an estimated 885 papers and books regarding mathematics and other disciplines, such as philosophy. Euler persisted to publish even after losing his vision, to which he is reported to have wittily remarked: “Now I will have fewer distractions.” Known for his diligence, Euler compensated for the loss of vision with his meticulous memory and acute mental calculations.

Euler spent his afternoons learning mathematical lessons from Johann Bernoulli, the foremost mathematician at that time. Influenced by his work, Euler made great advancements in calculus, geometry and trigonometry. However, his most popular work concerns exponentials and complex numbers. He devised an expression that is dubbed by a poll in the Mathematical Intelligencer as “the most beautiful theorem in mathematics.”
Recommended Video for you:
Euler’s Identity
Euler’s identity is an expression that lies at the heart of complex number theory. The expression raises a tantalizing query: what happens to a positive number when we raise it to an imaginary power?
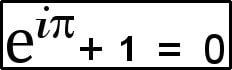
Why Is It So Important?
Euler’s highly revered expression is held to be the “gold standard of mathematical beauty” because it links seemingly different branches of mathematics in an exquisitely simple manner. Its ability to represent a deep fundamental mathematical truth with a 1-inch equation is what delights mathematicians all around the world.
Its aesthetics stem from the astonishing connection between mathematics’ fundamental identities and royal constants.
- The expression possesses Euler’s number ‘e’, the base of natural logarithms that is extensively recruited in calculus. It is a transcendental number whose value is 2.71828….
- It possesses ‘i’, the complex or imaginary unit, which is the square root of -1 or the solution of the function ‘x²+1=0’. It is of utmost importance in electrical engineering and has provided great insights in quantum mechanics.
- It possesses ‘π’, another transcendental number obtained by the ratio of a circle’s circumference to its diameter. Its value is 3.14159… This constant does not need any further introduction, as it is the most popular mathematical constant, ubiquitous in fields from Euclidian geometry to General Relativity.
- It possesses the first natural number ‘1’, the multiplicative identity — any number multiplied by this identity results in the same number itself.
- It possesses the first whole number ‘0’, the additive identity – any number added to this identity results in the same number itself.
In thereby combines mathematics’ five fundamental constants.
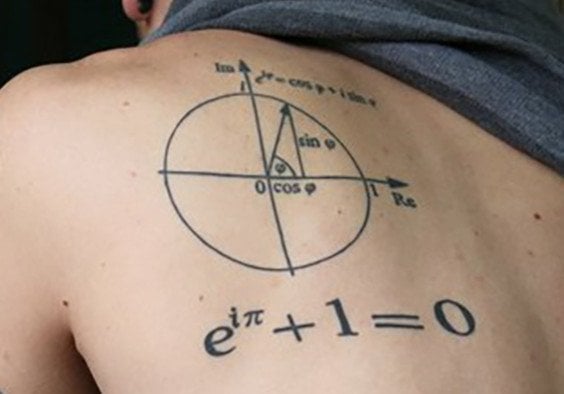
Enamored by this simple theorem, Stanford mathematics professor compared it to a Shakespearean sonnet “that captures the very essence of love, or a painting that brings out the beauty of the human form that is far more than just skin deep.” Even Richard Feynman couldn’t resist calling it “our jewel” and the “most remarkable formula in mathematics.”
A poll of readers conducted by Physics World named Euler’s identity alongside Maxwell’s equation as the “greatest equation ever.” Euler’s brilliance was so acclaimed that, in the poll conducted by Mathematical Intelligencer mentioned earlier, Euler was responsible for three out of top five expressions!
Proof
We can derive the expression with the help of two arguments. The first one relies on Taylor’s theory regarding the expansion of trigonometric functions. Taylor’s expansion is based on the principles of calculus. How the sequences are derived is irrelevant right now and beyond the scope of this article.
Originally, the exponential operation ‘x raised to power y’ was defined only when the value of y was positive (including between 0 and 1, which signified a root of x, such as x raised to half implies the square root of x). However, the Taylor series expansion linked two distinct areas, giving form to what is known as Euler’s formula. Those who are interested can find the detailed proof of how we arrived at Euler’s formula here.
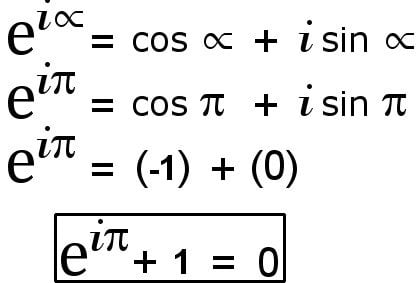
Euler’s identity is, therefore, a special case of Euler’s formula where the angle is 180º or π radians, such that the values on the righthand side become (-1) + 0 or simply, -1.
The second argument derives Euler’s formula graphically on a 2-D complex plane. A two-dimensional complex plane is composed of two axes. The horizontal axis is the real axis, which represents real numbers, while the vertical axis is the complex axis and represents all the complex numbers. A complex number on this plane is represented by ‘x + iy’.
On this plane, draw a circle of radius ‘1 unit’ with its center at the origin. Being a unit circle, the value of r — the radius of the circle this vector will draw — is here 1. Furthermore, when the complex number, represented by a vector touching the circle’s circumference, is rotated to the edge of the second quadrant, the angle it makes with the real axis is 180º or π radians.
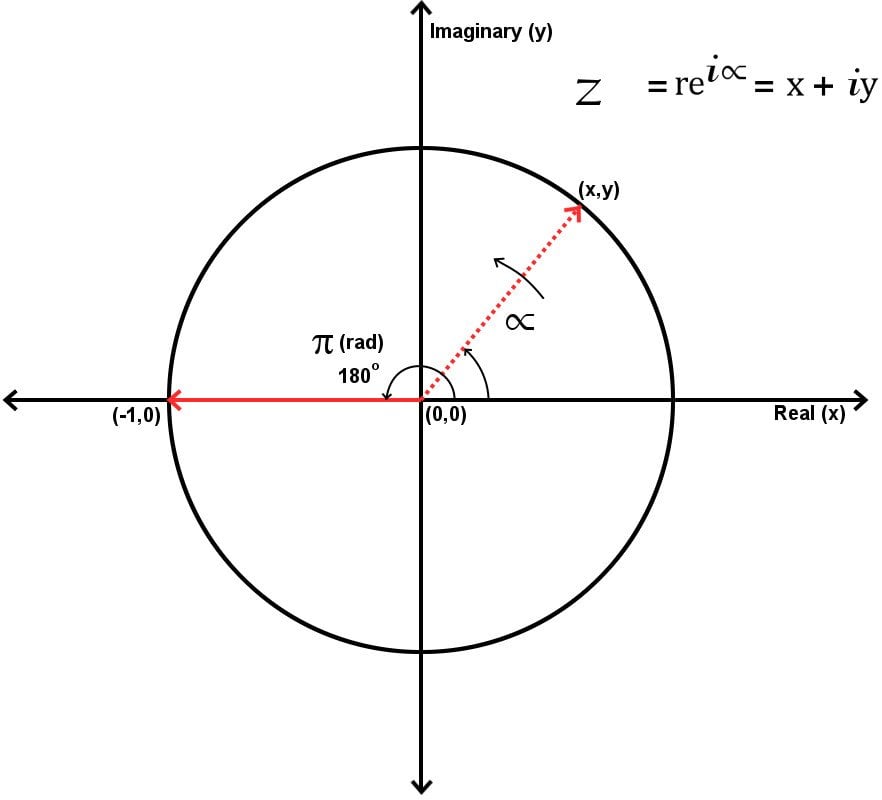
At the point where it touches the horizontal axis, its coordinates are (-1,0). Referring to the polar form of complex numbers, one can easily discern that