Table of Contents (click to expand)
The sanctity arises from how innocuous, yet influential, these numbers are. A new number in the pattern can be generated by simply adding the previous two numbers.
Mathematics is the study of patterns. While all patterns tend to conform to the stringent rules of logic, only a few of them foster creativity. It is absurd to me how a single, one-inch equation can momentarily possess your hand and lead you to draw the most exquisite of figures. It’s remarkable how these complex figures can be reduced to three symbols and two parallel lines. I use the term possess because, for this moment, we blindly do what the equations command, and trusting the prophecy, we begin to mark dots, which in the beginning seem unconnectable.
However, we continue to acquiesce. The tools clink and the obnoxious ruler refuses to be lifted until the impression on the paper is essentially a collection of infinite dots; black dots left by the pencil and white dots pecked by the compass. The infinite dots unlock themselves quickly and obediently align just as the logic requires them to. While the minimalist delights in a circle, the abstractionist delights in a polyhedron.
Then there are numerical patterns, a sequence of numbers that periodically repeat. Human beings are inherently pattern-seeking creatures. In fact, we are so adept at connecting the dots that these patterns aren’t exclusive to dots, but are also extended to contexts. The appearance of a pattern or figure with a vice or a virtue correlates the occurrence of the two. They have been the driving force behind cults in a myriad of societies.

There is an element of piousness that people have long associated with certain figures and groups, such as The Illuminati. On the other hand, scientists and mathematicians prefer to associate a form of intellectual mystery to such patterns. Consider the Wow! Signal, a pattern of alphabets received unexpectedly among numbers by Ohio’s Big Ear radio telescope, hinting at extraterrestrial activity.
However, there also exists a pattern of numbers that incites not merely mystery, but sanctity, for it emerges in places one would never expect. Consider this pattern — 13-3-2-21-1-1-8-5 — drawn by the murdered museum curator Jacques Saunière as a hint for Tom Hanks in The Da Vinci Code.
Recommended Video for you:
What Are Fibonacci Numbers?
The hint was a small, jumbled portion of numbers from the Fibonacci sequence. The sanctity arises from how innocuous, yet influential, these numbers are. A new number in the pattern can be generated by simply adding the previous two numbers. Starting from 0 and 1 (Fibonacci originally listed them starting from 1 and 1, but modern mathematicians prefer 0 and 1), we get:
0,1,1,2,3,5,8,13,21,34,55,89,144…610,987,1597…
We can find any ‘n’th digit in the sequence using this expression: xn=xn-1+xn-2
Fibonacci was known to be the most talented Western mathematician of the Middle Ages. Originally born as Leonardo Pisano, the name Fibonacci was coined by a French historian. The name, now quite popular in every household, is short for “Fillius Bonacci”, which translates to “son of Bonaccio”, where Bonaccio refers to his father.

Fibonacci was tremendously fascinated by Hindu-Arabic mathematics. Europeans at that time continued to use the extensive set of Roman numbers, while the Hindus and Arabs had been enjoying the virtues of the Hindu-Arabic number system — Base-10 numbers ranging from 0-9 — for generations. He decided to bring these ideas to Europe by publishing them in his highly revered work Liber Abaci.
The book became a legend. However, its popularity was eventually reduced to only two contributions: first, the number system, without which the advancements of modern mathematics would not have been possible; and second, a hypothetical, unrealistic problem about the breeding of rabbits. The Fibonacci numbers first featured as the solution to this problem.
The Mystery Of Fibonacci Numbers
However, there seems to be an inconsistency in abstract math. Doing abstract math is like counting the triangles in The Louvre. Sure, it’s fun to do, but is it of any use? However, it is in our nature to investigate. The predisposition to patternize, whether mathematically or behaviorally, cannot be neglected. Regardless of its futility, our fascination with patterns is persuasive enough to seek them.
Consider the Pisano Periods derived from the Fibonacci sequence. A Pisano Period, named after Fibonacci himself, is a set of numbers that cyclically repeat themselves. The numbers are remainders obtained from the division of Fibonacci numbers and a positive real number.

One can divide the sequence with any number to obtain such a cyclic pattern. For instance, when the numbers are divided by 7, a period of 16 numbers emerge. Similarly, the period’s length is 20 when the divisor is 5. Even dividing by 1/3 results in a long tape of recurring, identical snippets. However, mathematicians haven’t discovered a general formula that predicts the length of one period when the sequence is divided by a particular number.
Another raging perplexity is the infinite right-angled triangles hidden in the sequence. Starting with 5, every second number in the sequence is the hypotenuse of a right-angled triangle whose longer side is the sum of all sides of the preceding triangle and the shorter side is the difference between the skipped number and the shorter side of the preceding triangle. A pictorial explanation will help these triangles be better understood.
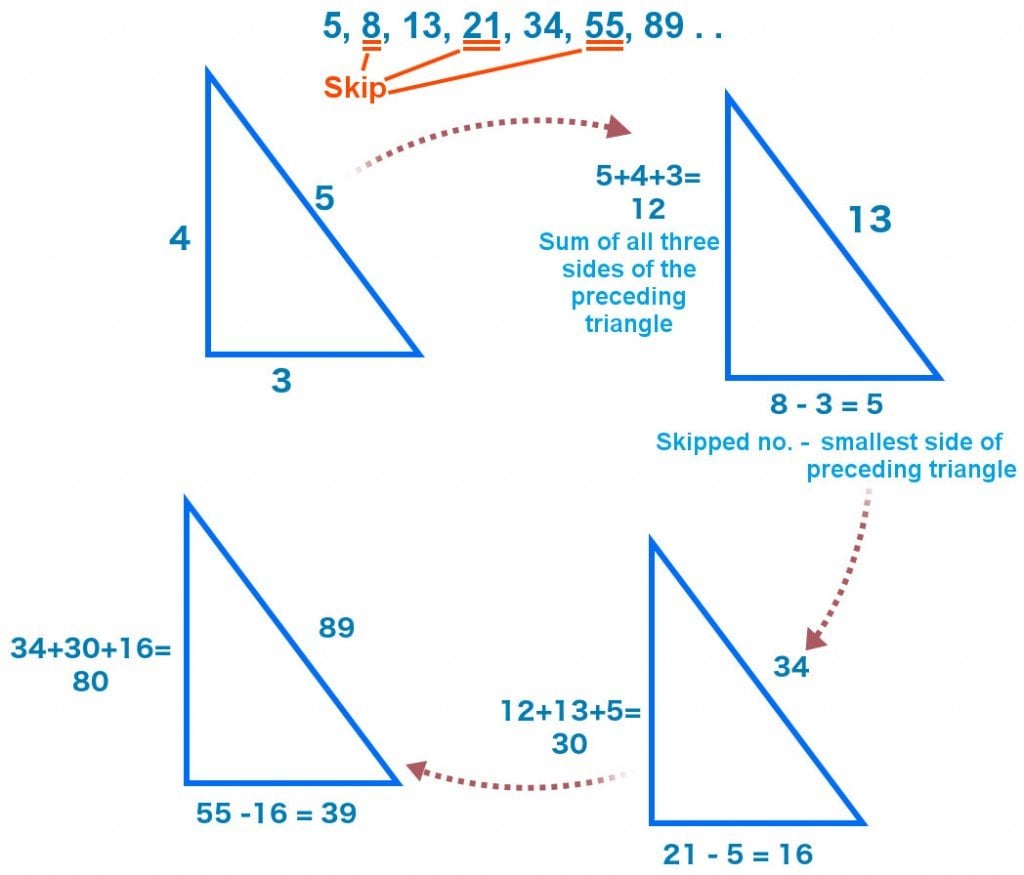
The utility of abstract math has been the primary argument in the debate questioning whether math was invented or discovered. There are theories that illustrate the highest order of mathematical genius and rigor but are utterly isolated from the real world. For instance, Newton invented calculus particularly to determine the equation of the trajectory that Earth was following around the Sun. Of course, calculus turned out to be lucrative in a myriad of other domains too, but can we say the same thing about Riemann’s Hypothesis?
However, there are rare instances where highly esoteric abstract math becomes applicable. For instance, Riemann developed his absurd concepts of curved geometry in the 1850s, which seemed inapplicable until Einstein used them to rediscover the laws of gravity in his General Theory of Relativity. The unpredictability of these mathematical marriages still perturbs us.
This is the case with the mystical nature of Fibonacci numbers too. Despite being discovered in the Middle Ages, they have been discovered and rediscovered, to everyone’s bewilderment, in places that we never expected. Our fascination with Fibonacci numbers extends to such an extent that an entire magazine is dedicated to its peculiarities, called the Fibonacci Quarterly.
Consider Pascal’s triangle. When Pascal was consulted by a gambler about the odds of the outcomes of a die and the nature of stakes, he invented the theory of probability to solve these problems. Pascal’s triangle is a neat triangle formed by binomial coefficients. The triangle acts as a table that one refers to while expanding the binomial equation.
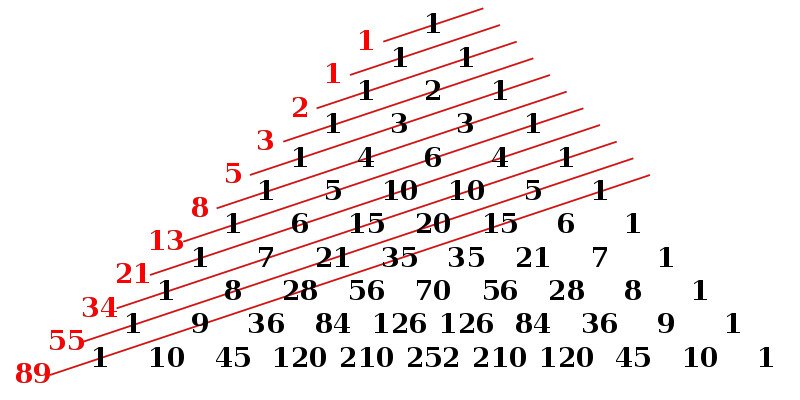
However, if you were to draw diagonals moving down the triangle and sum the numbers residing on each individual diagonal, then the series of numbers equated with each diagonal represent, as you might have guessed, the Fibonacci numbers. The theory of probability was founded 400 years after Liber Abaci was published.
Or, consider the Mandelbrot set, a mathematical function that can be limned by a beautiful diagram drawn in the complex plane. The diagram appears to be a heart-shaped leaf with tiny buds on its edges. These buds are suffused with incredibly thin thorns. The diagram represents a fractal, a structure whose every single part is made up of itself. Which means that if you were to keep zooming in on it, you’d find that the structure recurs in an infinite loop.
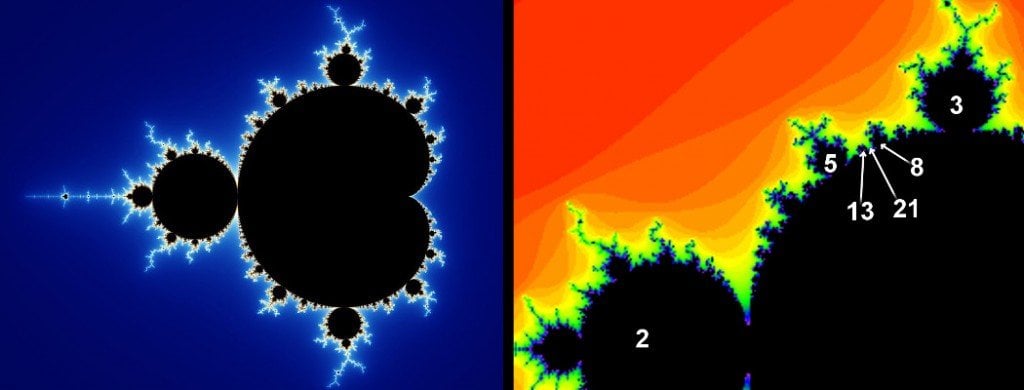
As we zoom into the buds on the edges, we see that the bud enlarges into the original leaf and three new buds emerge on its edges. If one were to keep zooming in, he would witness this procession go on and on forever. However, as we peek deeper and deeper, we observe that the number of thorns on every new bud increases. The increment in numbers mimics a certain pattern; it’s the Fibonacci sequence! Who could’ve possibly predicted this?
The sequence also turns up in economics and in tracing the pedigree of male bees. It is extensively used in computer science, where it is used to generate perceivably random numbers by algorithms called Pseudorandom Number Generators. I use perceivably because the generated numbers aren’t truly random; they always depend on a previous input.
It is also used in sorting algorithms in which dividing the area into proportions that are two consecutive Fibonacci numbers, and not two equal parts. This renders the hunting down of a location to the simplest mathematical operations — addition and subtraction. Whereas, binary sorting (dividing into two equal parts) requires the use of multiplication, division and bit shifting. The sequence is also used to derive various other important mathematical identities. However, its most important application is found in our gardens.
What Is The Fibonacci Spiral?
The Greeks always pondered whether there exists a factual description of beauty, an innate property or essence, as they called it, that would leave no room for subjectivity. For instance, a triangle can be defined as any three-sided body wherein the sum of all three angles formed between these sides must add to no more or less than 180 degrees. The growth of another side between two vertices, however small, sees that the body ceases to be a triangle. Could there be a similar exclusive criterion to judge the beauty of a daisy?

The Greeks did eventually discover this essence. According to them, the most beautiful way to divide a line into two parts is to divide them in a ratio such that the longer part divided by the shorter part is equal to the whole divided by the longer part. They called this the Golden Ratio, and its value is 1.618…
Consequently, they based their art and architecture on this ratio. An example is the architecture of The Parthenon, whose sides are in the Golden Ratio. Even Renaissance artists were in cahoots with each other about the use of this ratio. A plethora of their artwork relies on the ratio to amplify its aesthetic appeal.
What does this treasured ratio have to do with the Fibonacci numbers? Kepler once observed that “as 5 is to 8 so is 8 to 13, practically, and as 8 is to 13, so is 13 to 21 almost.” The ratio of two consecutive Fibonacci numbers is approximately equal to *incipient slow claps* the golden ratio! This links Fibonacci numbers to one of the most recognized spirals on the Internet.
The squares of Fibonacci numbers can be written like this:
1,1,4,9,25,64,169,441…
Nothing mysterious? Let’s add a bunch of them together:
1+1+4 = 6
1+1+4+9 = 15
1+1+4+9+25 = 40
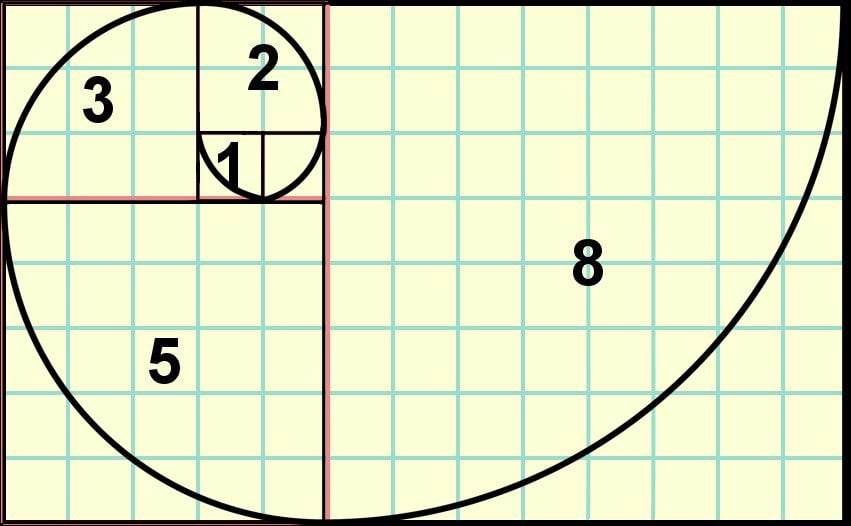
Look closer and you’ll notice that 6 is the product of 2 and 3, 15 a product of 3 and 5, and 40 a product of 5 and 8. A conjugal relationship between Fibonacci numbers and the golden ratio becomes conspicuous — the two numbers constituting these products are consecutive Fibonacci numbers! Now, let’s perform the above summation pictorially. Each number squared can be represented by a square whose side measures to be the same number of units that is being squared.
So, the square of one is represented by a square of side one unit. This square is then added to the next square in the sequence — another square of side one unit. Next, the 1×2 rectangle is added to a square of side two units, which is then further added to a square of side three units and so on. We realize that the products were actually the areas of these emerging rectangles.
Because the products were consecutive Fibonacci numbers, one can discern that the ratio of the two sides of any single rectangle is the golden ratio! As the number of sums approaches infinity, the ratio of sides of the incumbent growing rectangle approaches the ratio’s exact value. A curve emanating from the center and passing through every square’s corners gradually grows into a spiral – the golden spiral, steadily deviating at an angle called the golden angle.

The golden spiral can be found in a myriad of places in nature, from the shape of our galaxy to a nautilus shell. It governs the arrangement of pine cones and the fruitlets of a pineapple. My favorite is its occurence in the arrangement of seeds cluttered in the center of a sunflower. However, using the term “clutter” would be shamelessly overlooking the magnitude of rigor that nature spent while organizing these seeds.

The seeds aren’t aligned like the spokes of a wheel; they gradually digress outwards. The angle of digression is the golden angle. It seems that nature voluntarily opted for this ratio because dividing the circle by an irrational number caused no seed to have a neighbor at the same angle from the center. This resulted in highly efficient packing, leaving almost no room for negative space. The number of spirals, you ask? 55 in one direction, 89 in the other. Both Fibonacci numbers, of course!













