Table of Contents (click to expand)
A twin prime is a prime number that is either two less or two more than another prime number. A cousin prime is a prime number that differs from another by a gap of 4. A sexy prime is a prime number that differs from another by a gap of 6.
Numbers hold a certain sense of intrinsic beauty that most of us cannot deny. Even if you do fit in the cadre of people who feel an aversion towards numbers, there are still patterns that almost anyone can see. Today, we will be looking at a few such patterns that arise in the series of numbers known as primes. Now, before we step into investigating these patterns, let’s first take a brief overview of what prime numbers actually are.
Recommended Video for you:
Prime Numbers
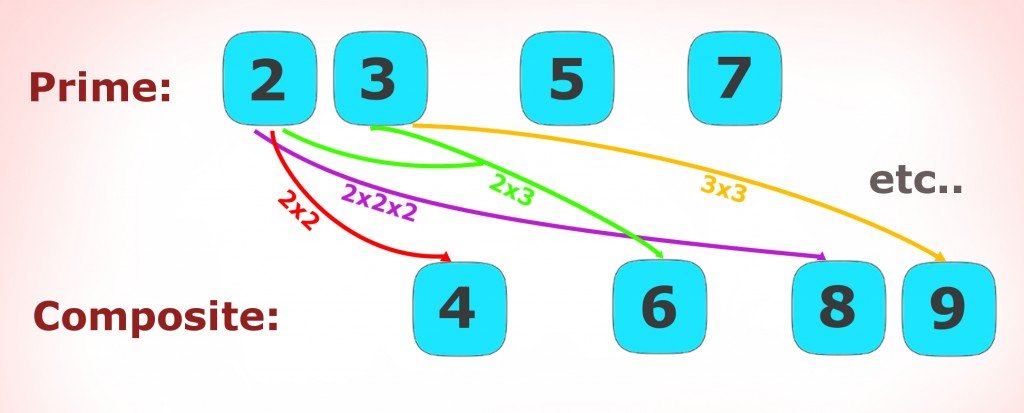
A prime number is a number that can be defined as a natural number. Without straying away too much from the topic at hand, a natural number can simply be defined as those numbers that are used for counting and ordering. To further elaborate, prime numbers are whole numbers greater than 1 that cannot be obtained as the product of any other whole number. It can only be obtained as the product of one and the number itself. Let’s take the example of two numbers—5 and 6. Now, 5 is a prime number because we cannot obtain it from the multiplication of any other whole number preceding it, such as 2 and 3. It can only be obtained by taking the product of 1 and 5 (the number itself). Now, the number 6 does not follow the definition of a prime. It can be obtained as the product of 2 and 3. It can also be obtained as the product of 1 and 6. Such a number that has more multiples apart from 1 and itself are known as composite numbers.
Twin Primes
A twin prime can be defined as a prime number that is either two less or two more than another prime number. Putting this in more simple terms, they are two primes that have a gap of two between them. What makes them highly unique is the fact that they become exceedingly rare as one examines larger ranges. It is still unknown as to whether there is an infinite number of infinite primes. Although substantial and pioneering work has been done by eminent mathematicians, such as Yitang Zhang, James Maynard and Terence Tao, it is still yet to be conclusively proven.

Now, let’s take a look at the first set of twin primes:
(3, 5), (5, 7), (11, 13), (17, 19), (29, 31), (41, 43), (59, 61), (71, 73), (101, 103), (107, 109), (137, 139), …
The unique property in the above pairs is that 5 is the only number to appear in two distinct twin prime numbers. We can only give a generalized form into which all twin primes fall, and that is (6n-1,6n+1) where n must be a natural number. The sum of all the twin pair numbers are divisible by 12. This applies to all twin pairs except the pair (3,5), as the sum of this pair is not divisible by 12.
Cousin Primes
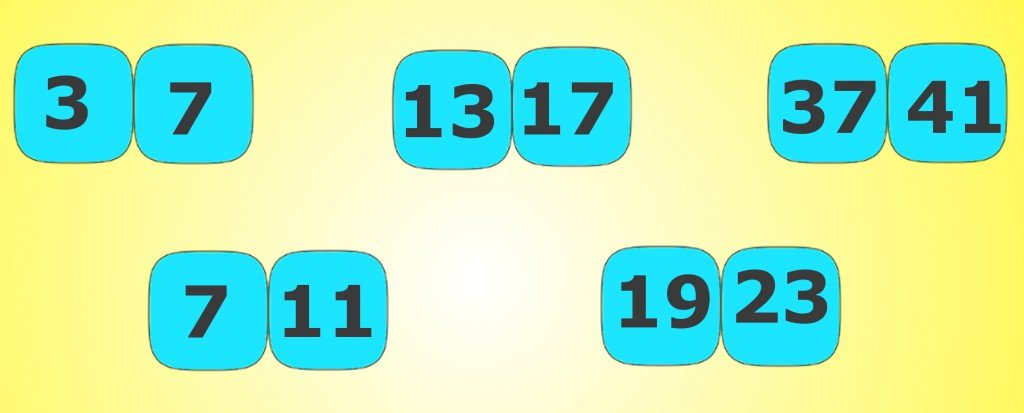
Cousin primes are those primary numbers that differ from another by a gap of 4. The only prime belonging to two pairs of cousin primes is 7. One of the numbers in n, n+4, and n+8 will always be divisible by 3, which makes it in such a way where n=3 is the only way all three numbers can be prime. Some of the cousin primes below 1000 are:
(3, 7), (7, 11), (13, 17), (19, 23), (37, 41), (43, 47), (67, 71), (79, 83), (97, 101), (103, 107), (109, 113), (127, 131), (163, 167), (193, 197), (223, 227), (229, 233), (277, 281), (307, 311), (313, 317), (349, 353), (379, 383), (397, 401), (439, 443), (457, 461), (463,467), (487, 491), (499, 503), (613, 617), (643, 647), (673, 677), (739, 743), (757, 761), (769, 773), (823, 827), (853, 857), (859, 863), (877, 881), (883, 887), (907, 911), (937, 941), (967, 971)
In the year 2009, the largest known cousin prime for (p, p+4) is:
p = (311778476 · 587502 · 9001# · (587502 · 9001# + 1) + 210)·(587502 · 9001# − 1)/35 + 1; where the term 9001# is known as a primorial. The term n# stands for the product of 2*3*5*7… of all primes lesser than or equal to n. In mathematics, and more particularly in number theory, a primorial is a function from natural numbers to natural numbers similar to the factorial function, but rather than successively multiplying positive integers, only prime numbers are multiplied.
Sexy Primes
In mathematics, sexy primes can be defined as those primes that differ from another by a gap of 6. An example of this is 5 and 11. A fun fact about sexy primes is that the name is a pun stemming from the Latin word for six, which is sex! In fact, unlike its predecessors, sexy primes come in what are known as constellations. There are three types of groupings for sexy primes.
The first kind of grouping is known as Sexy prime pairs. As the name suggests, these are primes that come in pairs. The sexy prime pairs under 500 are:
(5,11), (7,13), (11,17), (13,19), (17,23), (23,29), (31,37), (37,43), (41,47), (47,53), (53,59), (61,67), (67,73), (73,79), (83,89), (97,103), (101,107), (103,109), (107,113), (131,137), (151,157), (157,163), (167,173), (173,179), (191,197), (193,199), (223,229), (227,233), (233,239), (251,257), (257,263), (263,269), (271,277), (277,283), (307,313), (311,317), (331,337), (347,353), (353,359), (367,373), (373,379), (383,389), (433,439), (443,449), (457,463), (461,467).
As of May 2009, the largest known sexy prime was found by Ken Davis and has 11,593 digits. The primes are (p, p+6) for
p = (117924851 × 587502 × 9001# × (587502 × 9001# + 1) + 210) × (587502 × 9001# − 1)/35 + 5.
9001# = 2×3×5×…×9001 is a primorial, i.e., the product of primes ≤ 9001.
Sexy primes can be extended to larger constellations. Triplets of primes (p, p + 6, p + 12) such that p + 18 is composite are called sexy prime triplets. Those below 1000 are:
(5,11,17), (7,13,19), (17,23,29), (31,37,43), (47,53,59), (67,73,79), (97,103,109), (101,107,113), (151,157,163), (167,173,179), (227,233,239), (257,263,269), (271,277,283), (347,353,359), (367,373,379), (557,563,569), (587,593,599), (607,613,619), (647,653,659), (727,733,739), (941,947,953), (971,977,983).
As of 2013, the largest known sexy prime triplet, found by Ken Davis had 5,132 digits:
p = (84055657369 · 205881 · 4001# · (205881 · 4001# + 1) + 210) · (205881 · 4001# – 1) / 35 + 1.
Sexy prime quadruplets (p, p + 6, p + 12, p + 18) can only begin with primes ending in a 1 in their decimal representation (except for the quadruplet with p = 5). The sexy prime quadruplets below 1000 are:
(5,11,17,23), (11,17,23,29), (41,47,53,59), (61,67,73,79), (251,257,263,269), (601,607,613,619), (641,647,653,659).
In November 2005, the largest known sexy prime quadruplet, found by Jens Kruse Andersen, had 1,002 digits:
p = 411784973 · 2347# + 3301.
In September 2010, Ken Davis announced a 1,004-digit quadruplet with p = 23333 + 1582534968299.
There are also sexy prime quintuplets but for all practical purposes, our knowledge and inquiry up to sexy prime quadruplets would prove more than sufficient to tackle most math lectures you might be facing in number theory or prime numbers in general!













