Too tired to read? Listen on Spotify:
Prime numbers are used in cryptography because they are difficult to factorize. This means that it is difficult to find the prime factors of a composite number without knowing the factors to begin with. This makes it difficult for someone to intercept a message and read it without the proper key.
A hacker or thief attempting to crack a 400-digit encryption code that obscures your credit card details, with a computer that tests 1 million combinations per second, would take around 10 raised to the power 194 seconds to accomplish the feat. The Universe is 10 raised to the power 18 seconds old. As far as I know, cracking such a code then seems to be quite a tedious task.
When Fermat, primarily known for Fermat’s Last Theorem, discovered a subtle method to determine whether a number is prime or composite, his peers couldn’t comprehend the proof’s utility. The proof, for most of its existence, was perceived as a statue is – beautiful, but utterly useless. In fact, discoveries regarding prime numbers were venerated for merely the essence of discovery — for disclosing and making sense of the hidden complexities in mathematics, for solving a curious puzzle — except that they didn’t contribute any substantial solutions to the problems of the real world.
This was until 400 years later when the Internet was born, and the privacy of its billion users, from the content of confidential emails to transactions on e-commerce websites, relied solely on prime numbers.
Recommended Video for you:
Trapdoor
Prime numbers are commonly referred to as the “atoms” of the numerical realm, for they are the fundamental, indivisible units that make up every number. For instance, 10 can be written as a product of 2 and 5, two prime numbers. Or, 150 as a product of 15 and 10, which can be further broken down and written as the product of 3, 5, 2 and 5 – all prime numbers. Or, a larger number such as 126, 356, which is composed of larger prime numbers 2,2,31 and 1019.
This process of reducing a composite number to a product of prime numbers is known as prime factorization. For a computer, multiplying two prime numbers, each even 100 digits long, isn’t that difficult, however, factorizing the product back into its components is notoriously difficult, even for supercomputers. It is this shortcoming that Rivest, Shamir and Adleman exploited to create RSA encryption in 1977. In cryptography jargon, this unidirectionality is known as a “trapdoor”.

The Keys
Let’s say that C is a product of two prime numbers P and Q. While encrypting, say, your credit card details, the number C is used to generate the “public” key. This key, as its name suggests, is available to the public, meaning that it can be intercepted and read by anyone in the network. Banks are known to use public keys that are 617 digits long to secure your private transactions.
A public key secures private information by locking it in a box whose handles are tightly clasped with a several hundred-digit combination-lock. The box itself can be accessed by anyone, but the content inside it can’t. While a thief may furtively steal the box, he can’t unlock it without knowing the combination, without possessing the “private” key. This private key is only possessed by the sender and receiver of the content — the bank and you, the proprietor of the credit card.
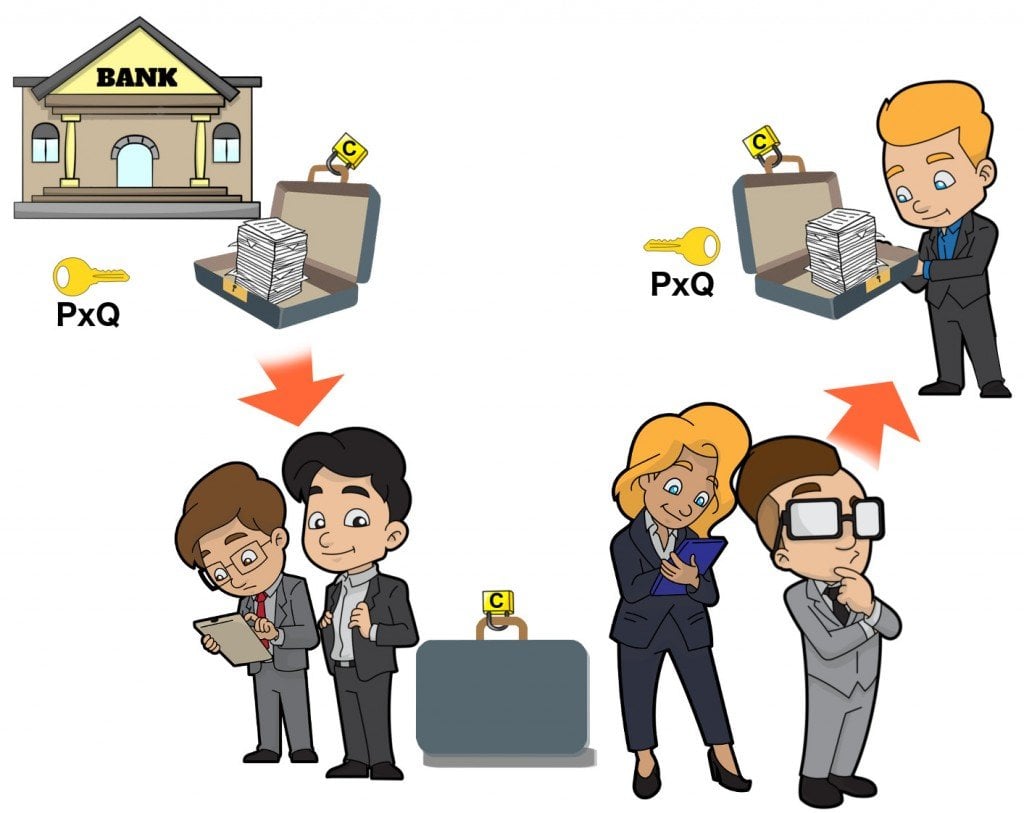
The private key constitutes the two prime numbers P and Q, which were multiplied to produce C, the public key. Without their knowledge, the thief, to peek in, must factorize C, which could take him thousands of years if the numbers are hundreds of digits long. And trust me, there are a lot of huge prime numbers. The largest I found is 2 raised to the power 43,112,609 subtracted by 1 whose primality was verified by a computer. If you were to write this number on an A4-size paper, it would take you a total of 4376 papers, yes, a tremendously thick stack of 4,376 papers, to complete the sequence.
Lastly, factorization is not impossible; it can be done. It is just exorbitantly time-consuming. As technology progresses, we might be able to crunch numbers more quickly. Quantum computers might be highly successful in achieving this, but currently, there are years, and probably decades, before they become fully-functional and ubiquitous. The largest numbers a computer drudgingly factorized into their primes were, 2 raised to the power 512 and recently, 2 raised to the power 768-digit long. Messages are encrypted by 2 raised to the power 1024-digit long public keys, some even by a 2 raised to the power 2048-digit long public key. So, don’t worry, your drunk texts are in safe hands.













