Table of Contents (click to expand)
You can count on your fingers up to 1023.
One mathematical tool that we always carry around with us is our hands. As the most basic form of a calculator, it lets us count in a number of ways. However, it’s rather useless to only have the power of counting just 10 digits. Imagine if you wanted to count the number of hairs on Trump’s head; you’d need more fingers, although not too many. We’re not saying that you NEED to do that, but it’s rather nice to have the option.
Recommended Video for you:
Rookie: 10
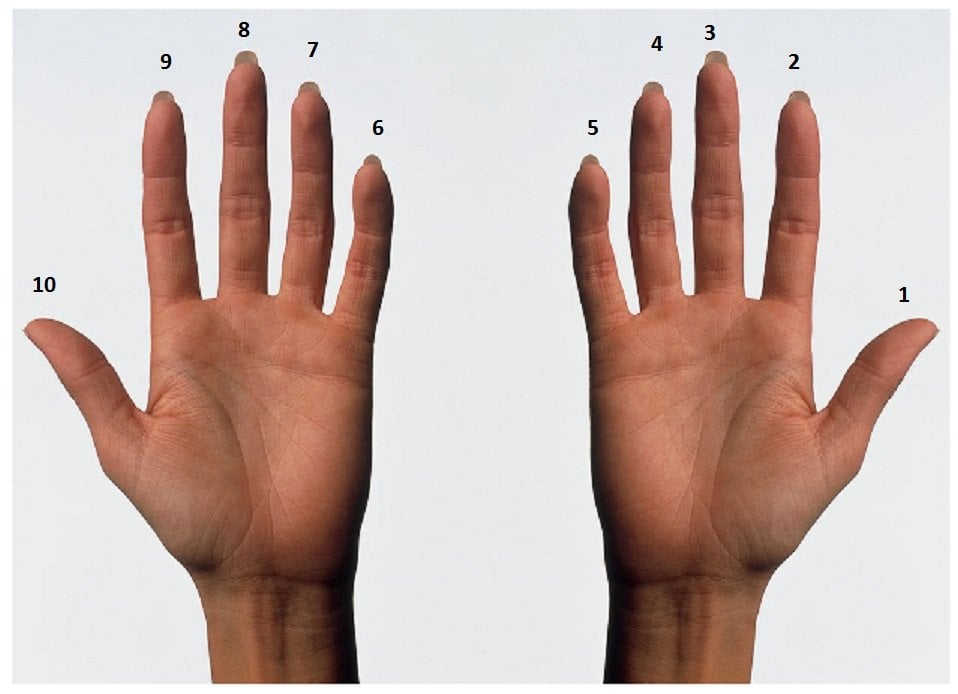
The human hand has 5 fingers, or to be precise, one thumb and four fingers. So, with both hands, it’s very easy to count to 10. In this case, there’s no particular order in which an individual assigns a value to a particular finger. The little finger on his left hand could very well be 5 or 6, according to each person’s preference. The only requirement is that the individual never repeats the use of the same finger.
Amateur: 24
Most people probably use the three segments (knuckle spaces) on their fingers to count even higher. Each segment would count as one number, bringing the highest possible count to 12 when using 4 fingers on each hand. In this method, there is also no preference for any particular finger, although the individual is required to follow a single direction, namely up-down or down-up, to avoid errors.
Professional: 576
In some cultures, people assign one of their hands as a counter for the other hand! What this means is that, they assign one of their hands, let’s say their left hand, as the ‘strong’ counter, while the right hand is the ‘weak’ counter. The individual begins counting segments on his weak hand and, after he reaches 12, he touches the first segment on the strong counter. At that point, he counts back from 1 to 12 on his weak counter, all while touching the first segment on his strong hand. After he has 12 on the weak hand, he moves down one segment on his strong hand. This allows him to count to 12×12=144.
This technique is improved if he decides to use the segments as well as the creases on his finger that separate the segments. Every human finger has three segments, meaning that there are three lines to divide them. If we also count those lines as units, we would get 6×4=24 units on each hand, giving us the ability to count to 24×24=576!
Expert: 1023
Now we’re getting into some serious mathematics within the art of finger counting. Most ‘brilliant’ mathematicians who showcase a talent for mental computing use the technique of ‘Positional Notation’. What this means is that every number in our decimal system uses a position of power (base)- 10 to represent itself. All of the numbers that we use in daily life are just a set of digits multiplied to powers of 10 and later added.
For example: 257 in our commonly used decimal system is actually 2×100+5×10+7×1, which is ordered using 102, 101, 100 etc.
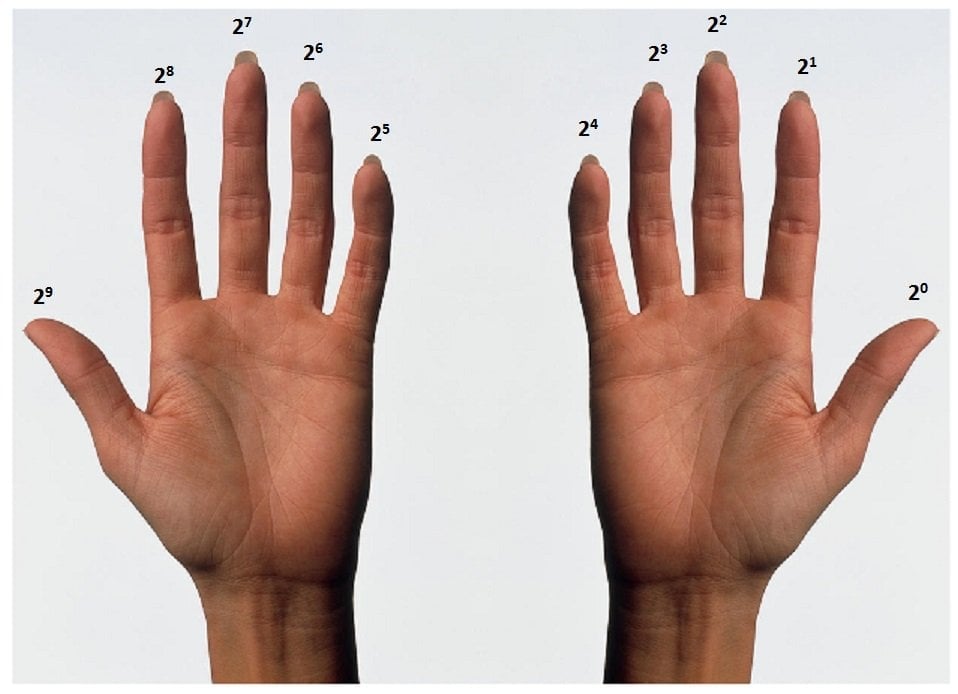
Similarly, if the base were to be 2, as in binary language, then 86 would be represented as 1010110, which translates to 1×26+0x25+1×24+0x23+1×22+1×21+0x20
Since our fingers can only have two positions – open and closed – counting base 10 is difficult, if not impossible. We can use the binary system in which powers of 2 are assigned to the fingers and 1 represents an open finger, while 0 represents a closed finger. This method can allow you to calculate up to the number that is the sum of the initial 10 powers of 2 (all fingers open). Hence, its upper limit is 1+2+4+8+16+32+64+128+256+512=1023 which happens only when all of our fingers are ‘open’.
Computers use this system of binary positioning to understand everything, since they can only interpret whether a signal is HIGH or LOW. High is understood to be 1, whereas Low is understood to be 0. This just goes on to prove that every calculation, no matter how hard it may seem, can actually be done using the binary system, but not with our fingers alone!

Considering all the useful applications to this technique of positional calculation, we should also mention its drawbacks. Let’s say you have to buy 4 bananas. Putting up 4 fingers to show how many you want is pretty straightforward, because it has a real meaning imprinted in our brains. Putting up just the middle finger to signify 22 is unnatural because we don’t identify it the same way. It’s rather rude too, if you think about it.
However, it does have the potential to simplify basic math with older children. Counting in binary on your fingers means that you can calculate sums and differences larger than ten and multiply quickly by two and powers of two.

Savant: Infinity!
If a person is dexterous enough to assign even a half-bend as a possibility of finger-bending, they could significantly increase their counting prowess. Since the base would now be 3, it would be possible to count up to a total of 310-1, which is 59058!
So, it might now be apparent that we can count as high as the number of recognizable shapes we can make with our fingers. These methods rely on the fact that we need visual cues in the form of the shapes that our fingers take. If we could simply bypass this condition and use only our sense of touch, we could count even further with relative ease.
For example, if we use our thumbs to assign the sides of our fingers different values, we could increase the number of countable units. Although the accuracy for this counting process decreases as we move onto higher numbers, the fact that we can theoretically do it is pretty amazing!