Why Is The Factorial Of Zero Equal To One?

The factorial of zero is one because there is only one way to arrange zero number of objects.

The query is reminiscent of why a number raised to the power zero is equal to one, a query I resolved in an earlier article. Also, let me reassure what I have previously assured while explaining that obvious, shamelessly taken-for-granted, yet inexplicable fact – the relation is not arbitrary.

There are three ways to delineate why the factorial of zero is equal to one.

Recommended Video for you:

Complete The Pattern

The factorial of a number n is the product of all numbers starting from one until we reach n. The operation is denoted by an exclamation mark succeeding the number whose factorial we wish to seek, such that the factorial of n is represented by n!. Numerically, the trails of multiplication can be illustrated in this manner:

1! = 1*1 = 1

2! = 1*2 = 2

3! = 1*2*3 = 6

4! = 1*2*3*4 = 24

.

.

.

If, (n-1)! = 1*2*3*4…(n-3)*(n-2)*(n-1)

Then, logically, n! = 1*2*3*4…(n-3)*(n-2)*(n-1)*n

Or, n! = n*(n-1)! – (i)

If you look at these trails carefully, a pattern will reveal itself. Let’s complete it until it manages to produce legitimate results:

4!/4 = 3!

3!/3 = 2!

2!/2 = 1!

1!/1 = 0!

Or, 0! = 1

One can arrive at this result by simply plugging in 1 for ‘n’ in (i) to get:

1! = 1*(1-1)!

1 = 1*0!

Or, 0! = 1

However, this explanation tells us nothing about why factorials of negative numbers cannot exist. Let’s turn towards our pattern again to find out why.

.

.

2!/2 = 1!

1!/1 = 0!

0!/0 = …uh-oh

I’d agree that these methods are a little fishy; they are seemingly sly, implicit ways to determine the factorial of zero. It is like arguing in favor of a straw-man. However, one can find an explanation in a field whose entire existence hinges on calculating factorials — combinatorics.

Arrangements

It was known as early as the 12^th century that there are n! ways to arrange n number of different objects. This act of arranging objects is known as a permutation. Let me give you a simple example to explain why there are n! ways to arrange n objects.

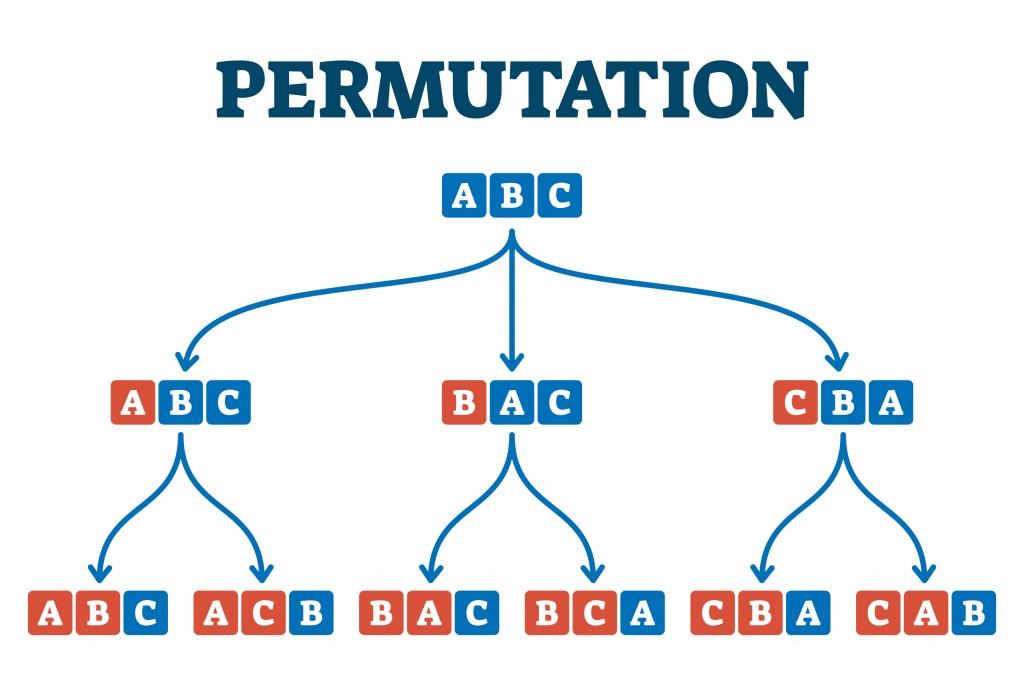
Consider 4 chairs that must be occupied by 4 people. The first chair can be occupied by any one of these four people, such that the resulting number of choices are 4. Now, that one chair is occupied, we have 3 choices that are potential occupants for the next chair. Similarly, the next chair presents two choices, and the last chair presents a single choice; it is occupied by the last man standing. Therefore, the total number of choices we have are 4x3x2x1 or 4!. Or, one can say that there are 4! ways to arrange 4 distinct chairs.

Thus, when the value of ‘n’ is equal to zero, the question translates to what are the different ways in which one can arrange zero number of objects? One, of course! There is only one permutation or one way to arrange nothing because there is nothing to arrange itself. WHAT? Honestly, this pertains to a branch of philosophy, albeit one of the obnoxious or phony notions that freshmen pontificate about after reading Nietzsche quotes on Pinterest.

Let’s consider an example that involves physical objects, as it might make for a better understanding. Factorials are also central to computing combinations – a process that also determines arrangements, but unlike permutation, the order of things is irrelevant. The difference between permutation and combination is the difference between a coded lock and a bowl bearing a mélange of diced fruits. Coded locks are often wrongly called “combination locks” when they should actually be called permutation locks, since 123 and 321 cannot both unlock it.

A general formula to determine the number of ways ‘k’ objects can be arranged amongst ‘n’ places is:

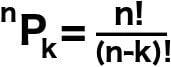
Whereas, to determine the numbers of ways to choose or combine ‘k’ objects from ‘n’ objects is:

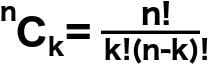
This allows us to, say, determine the number of ways in which two balls can be selected from a bag that contains five balls of different colors. Because the order of the selected balls is not important, we refer to the second formula for computing the entailed combinations.

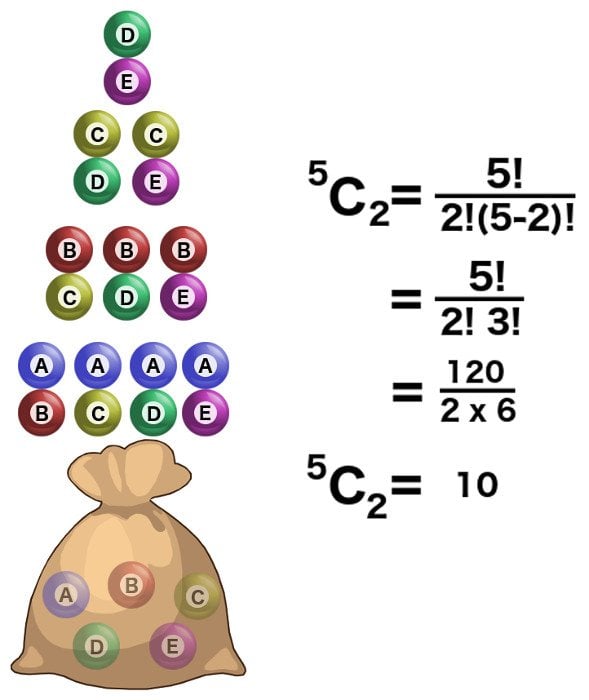
Now, what if the values of ‘n’ and ‘k’ are exactly same? Let’s substitute these values and find out. We observe that the factorial of zero is obtained in the denominator.

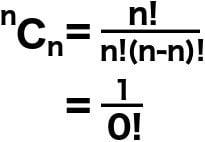
But how do we comprehend this mathematical calculation visually, in terms of our example? The calculation is essentially a solution to a question that asks: what are the different number of ways in which we can choose three balls from a bag that contains only three balls? Well, one of course! Picking them in any order would not make a difference! Equate the calculation with one and the factorial of zero turns out to be *drum roll*…… one!