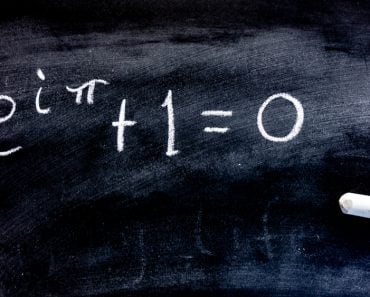Computers calculate the value of Pi up to trillions of digits by making use of infinite series formulas that have been developed by mathematicians.
The movie ‘Life of Pi’ was released in 2012. Back then, there was a scene in the film that puzzled me every time. It’s the part where Piscine Patel tries and succeeds, to establish the short form of his name to ‘Pi’. I remember thinking every time I saw it, “So he wrote hundreds of digits of 
on the board, that’s easy. You just keep dividing 22 by 7 in your head. I could have done that!”
But as I grew older, I realized how wrong I was. He wasn’t just dividing 22 by 7 in his head. He had memorized the value of up to hundreds of digits (see, now that is impressive). 22/7 is simply an approximation for , and will only give an accurate value till two decimal places ( = 3.14159265……. whereas, 22/7 = 3.1428571……).
Recommended Video for you:
How Do We Calculate The Value Of Pi?
Let’s say you have a circle (if not, just construct one). Measure its diameter using a scale and its circumference using a string. Now, if you divide the value of circumference by the diameter, you will probably get the quotient as 3.1415… (approx.). You will also observe that the division is never-ending. This is a value called Pi (). If we represent this mathematically,
Circumference of circle = 2 r
Diameter of circle = 2 r
So, Circumference/Diameter = (2 r) / (2 r) =
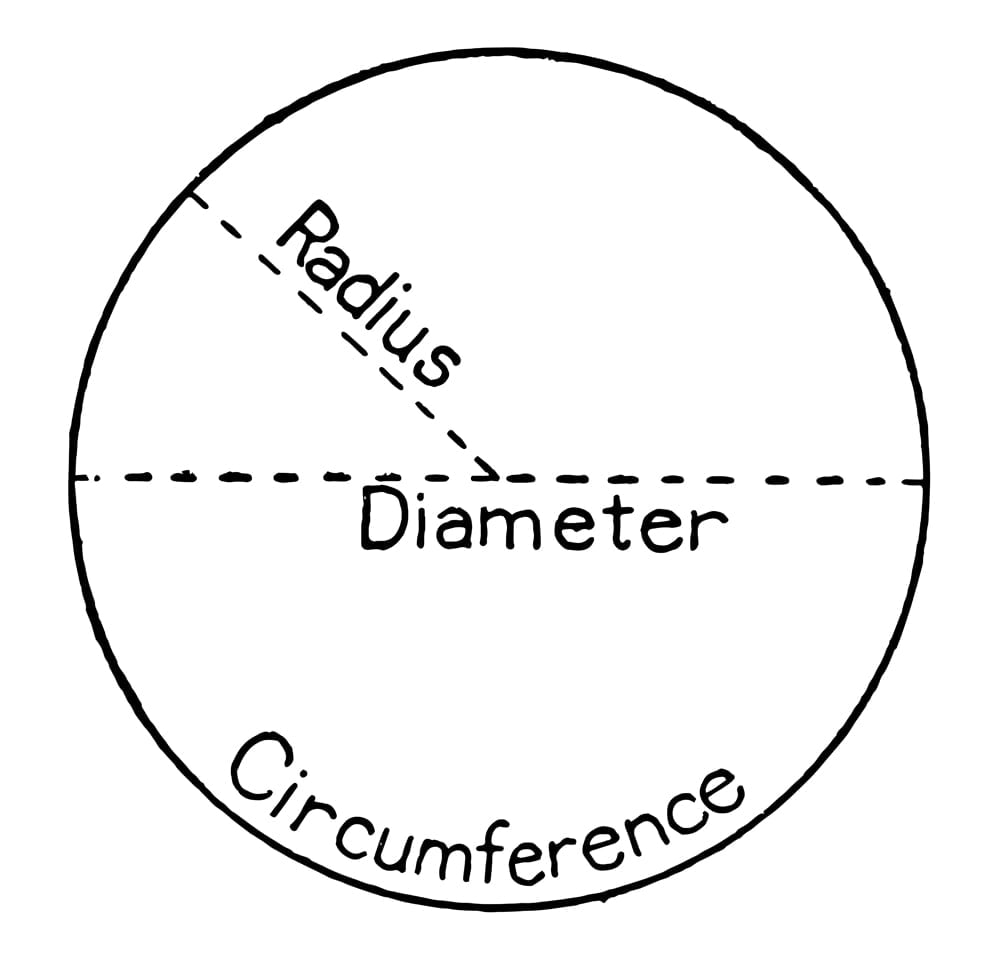
The method of measurements used above is how Babylonians and Greeks discovered it thousands of years ago. Since then, many approximations have been made about the value of this number.
However, even today, when we have calculated about 2.7 trillion digits of , we are nowhere close to the precise value. A number of books use the fraction 22/7 as the value of , yet even that is simply an approximation (in fact, 22/7 is closer to the actual value of than 3.14 is).
Why Don’t We Have The Precise Value Of Pi?
The truth is, we don’t know the precise value of because it is an irrational number.
An irrational number is a number that can not be represented in the form of a fraction. The digits after the decimal are never-ending and non- recurring, i.e., they don’t appear in a particular sequence. That is also the reason why 22/7 is only an approximation for and not its real value.
Now, if we don’t even know all the digits of , how are computers able to calculate them for us? After all, computers are programmed by humans themselves, right?
The answer to that is yes, computers are programmed by humans. But we need to understand exactly how computers work, in order to figure out this answer.
How Do Computers Work?
Computers basically work on algorithms. A computer is simply a machine. And a machine doesn’t make decisions on its own as we do. It works according to a set of instructions or steps that we feed into it. And it follows these sets of instructions until we tell it to stop. Of course, it wouldn’t be able to stop on its own, since it does not have the ability to make that decision.
Also, remember that is a number with infinite decimal places. This means that if we are to calculate the value of using a computer, it will have to follow a set of instructions an infinite number of times, since the digits of go on forever.
So, this means, if somehow, we are able to figure out this set of instructions that generate the precise value of if it is computed an infinite number of times, then the computer can do the entire calculation by itself. And it will keep calculating until we give the instruction to stop.
What Is The Algorithm For Our Calculation?
In our case, this set of operations is called an infinite series. An infinite series is an infinite sequence of values that follow a particular rule throughout.
For example, we have the series-
1/2, 1/4, 1/8…….
Each term here is multiplied by half of the previous term.
If we add them,
This is termed as an infinite series. It can be written in short using the symbol ‘sigma’: –
In this case, the addition of all terms S amounts to 1. In case you are confused as to how it can be 1, here is an illustration of the proof:
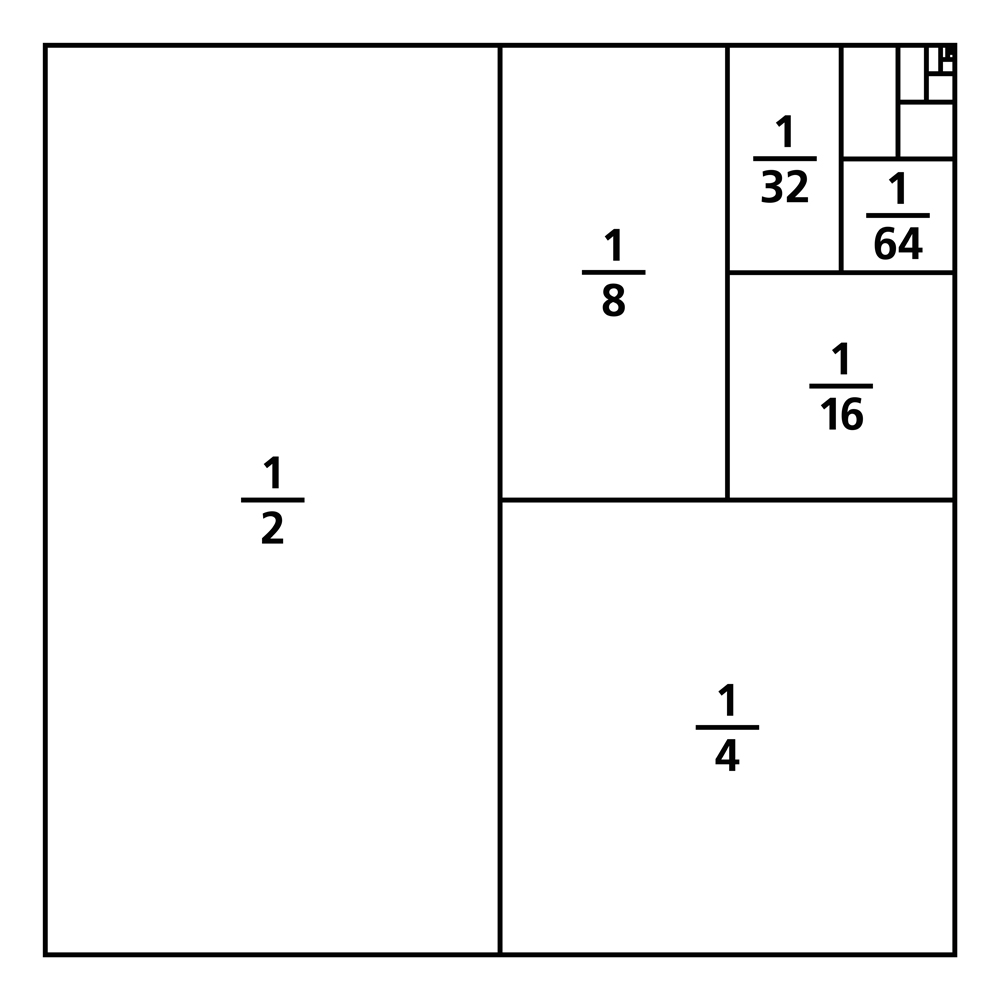
Now, if we are able to find an infinite series such that the value of ‘S’ in the above equation equals pi, we will have found an algorithm to generate the value of pi. After that, all we would need to do is feed this algorithm into the computer.
There are numerous series today that are used to generate the value of pi. One of the most well- known and simplest series to calculate is the Gregory- Leibniz Series :
With this series, you will be able to calculate /4 exactly. Then if you multiply that by 4, you will have the value of . The only problem with this series is that it is not very efficient. You will have to add a lot of terms if you wish to get an accurate value (Around 300 terms in order to compute till 2 decimal places). That is a lot of time- consuming work, even for a computer.
Another series that is more efficient than the one given above is Nilakantha Series:-
These are only some of the simplest of formulas that can be used to calculate . There are other, more efficient, series developed by mathematicians that can be used to calculate this value using computers- like the algorithm of Brent and Salamin.
Imagine an extremely efficient infinite series and a super-fast computer. That’s how the value of has been calculated to trillions of digits today. The world record for calculating the most number of digits of is held by Timothy Mullican. He computed 50 trillion digits of on his personal computer (as of 30th January 2020).
We have certainly made plenty of progress, from calculating this value by hand to using super- slow computers in the 1950s (which were, actually, the most efficient computers of the time), to this day, where computers can calculate in mere seconds.
