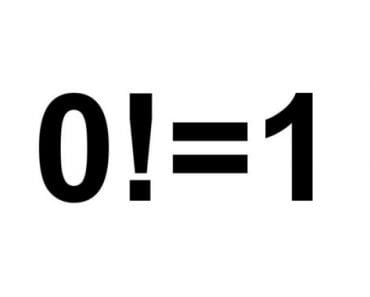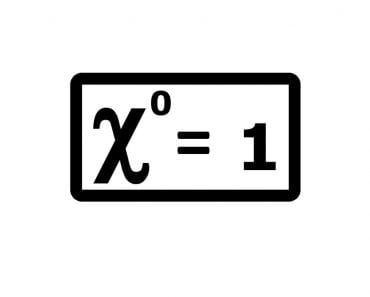The Four Fours Puzzle is a challenge to create every whole number from 0 to infinity using mathematical expressions that only consist of four fours manipulated by any number of mathematical operations.
Do you like challenges? Do you often pride yourself on your mathematical brilliance? Do you always act indignant or chagrined, but secretly love the accusations of being a nerd? If yes, then this challenge is for you.
The four fours problem was published in the “Mathematical Recreations and Essays” written by W.W Rouse Ball in 1914, who nonchalantly described the problem as “tradition recreation”. However, the whimsical puzzle is known to have been first conjured in the 19th century, and its popularity was at its zenith around 1890. Gradually, it grew less well known, until Rouse published his essays and revived interest in the puzzle.
The puzzle slowly grew into an intellectual pastime. Even Paul Dirac, the Nobel Prize-winning physicist who discovered anti-particles and is widely lauded for his mathematical genius alongside Richard Feynman, gave it a try and, as one would expect, he solved it. Or, rather, as we’ll eventually find out, he hacked it.
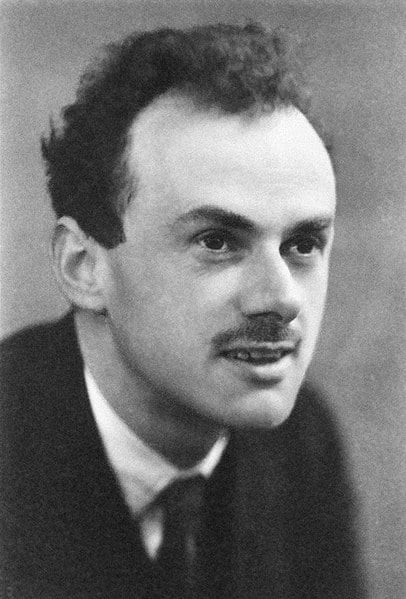
Recommended Video for you:
The Rules
The rules are simple: create every whole number from 0 to possibly infinity using mathematical expressions that only consist of four fours manipulated by any number of mathematical operations. For instance, 
can be expressed as 
, while 
can be expressed as 
and 
as 
(remember that according to BODMAS, the division occurs before the subtraction) and so on to the largest number you can create. Also, like a snippet of code, more space and time-efficient expressions are favored. For instance, can be expressed even more succinctly as 
.
However, the four basic operations can only create a handful of numbers. Therefore, we must turn to other operations. This would include concatenation or the combination of two numbers to form a larger number such as
, factorials such as 
, decimal points 
, square roots 
, exponential and consequently logarithms. These operations allow us to express numbers to infinity!
For instance, 47 can be expressed as (again, BODMAS says division must occur first). Or, and this is brilliant, 49 can be expressed as 
. Try it out, it really is 49! Also, because we cannot use any other number, even the decimalized is written as and not 
.
Some even resort to summoning absurd or atypical operations, such as the percentage or even permutation and combination (4P4 and 4C4). For instance, 99 can be expressed as 
, which is 100 – 1 or 99. However, traditionalists might call the introduction of atypical operations cheating or sophistic. A sophist is someone who reasons with clever – but false – arguments.
The methods are clever, but not entirely false. What perturbs some people is that these novel methods simplify the puzzle, which takes the fun out of it, like playing basketball with a midget hoop. Also, if these tricks weren’t enough, mathematicians devised a formula that enabled them to express numbers to infinity. Dirac is rumored to have arrived at the same generalization when he confronted the puzzle, and was thus accused of hacking it.
The Hack
The hack relies on one of the most common but least understood operations – logarithm. Let me first remind you how logarithms work. If 
, then 
. For instance, 
, therefore, 
.
Now, the rules demand that we only use the number 4, so the base of logarithms we employ must be limited to 4. For instance, if 
, then 
. Or, if 
, then 
. One can discern the emergence of a pattern here – 
. Let’s denote this expression by X. Even if you don’t understand the working principle of logarithms, just remember this formula to get through the rest of the article.
The value of n in X doesn’t even have to be a whole number. This characteristic is crucial for the hack. Now, the article gets slightly more complicated from here, so a moderate degree of grit is expected from the reader. Let’s plug in ½ in place of n, in X, which translates to 
or . We see that X becomes ½. Similarly, the value of X for n = ¼ or 
is ¼ and then 1/8 when n is 1/8 and so on.
Now, let’s perform the same logarithmic operation X, but replace 4 with ½. For instance, 
and 
or 
and 
or 
and so on. You can practically smell the hack from here.
The numbers on the right side of the equal sign increment each time we increment the number ½ is raised to. This incrementation could reach infinity if we were to increment the power on ½ ad infinitum.
If we express the operation on the left with four fours, we would solve or “hack” the puzzle.
Refer to X again and you will realize that the powers of 
namely, 
can be expressed with X itself! Now, X uses two fours, so we need the remaining two to solve the puzzle. These two fours arise from our need to express the base of the logarithm, which is , in terms of four, as the use of is against the rules. Let’s find a way to express in terms of fours. Now, can be written as 
, which is nothing but 
. And there, we have solved it.
.
.
.
If exponentials weren’t enough, adroit mathematicians used logarithms to solve it. This generalization or formula to produce any natural number essentially vanquishes the puzzle once and for all. To produce any number, one must plug in the formula, the square root of 4 taken for the same number of times. Given a page long enough, one billion or even infinity can be produced by taking the square root of 4 a billion or an infinite number of times. For this reason, logarithms have been banned as a viable solution to solve the puzzle. However, some mathematicians also despise this hack because it looks ugly.
The puzzle has been used for years by puzzle lovers to pass the time during long journeys on trains or flights. Now, even newer versions of the puzzle have been developed, versions that might require superior mathematical acuity – the five fives or six sixes puzzles! But do you have what it takes?
