Table of Contents (click to expand)
Ptolemy’s theorem states, ‘For any cyclic quadrilateral, the product of its diagonals is equal to the sum of the product of each pair of opposite sides’. The theorem can be further extended to prove the golden ratio relation between the sides of a pentagon to its diagonal, and the Pythagorean theorem, among other things.
Have you ever wondered what Michelangelo’s Holy Family, a man inscribed in a pentagram by Heinrich Agrippa, and The Last Supper by Salvador Dali have in common?
Apart from being timeless artistic wonders, all of these follow a common design philosophy/element. Each contains the form of a pentagon, and the ratio of any regular pentagon side to its diagonal yields the ‘Golden Ratio’ (1.618033…). Man-made constructs and natural items that follow the golden ratio in their construction are considered to be some of the most aesthetically pleasing things in the world.
This aesthetic relation between the diagonals and sides of a pentagon can be proven by extending Plotemy’s Theorem of cyclic quadrilaterals. Along with that, Ptolemy’s Theorem can also be used to prove the Pythagorean theorem, but before we get to all that, what is Ptolemy’s Theorem?
Recommended Video for you:
Ptolemy’s Theorem
Claudius Ptolemy was a Greek legend with expertise in multiple fields; while he was most popular for his work in astronomy (Ptolemaic system), he was also a profound math wizard and discovered a theorem now known as ‘Ptolemy’s Theorem’. The theorem was mentioned in Chapter 10 of Book 1 of Ptolemy’s Almagest and relates the four sides of a cyclic quadrilateral (a quadrilateral with all four vertices on a single circle) to its diagonals.
Ptolemy’s Theorem states, ‘For a quadrilateral inscribed in a circle, the sum of the products of each pair of opposite sides is equal to the product of its two diagonals’.
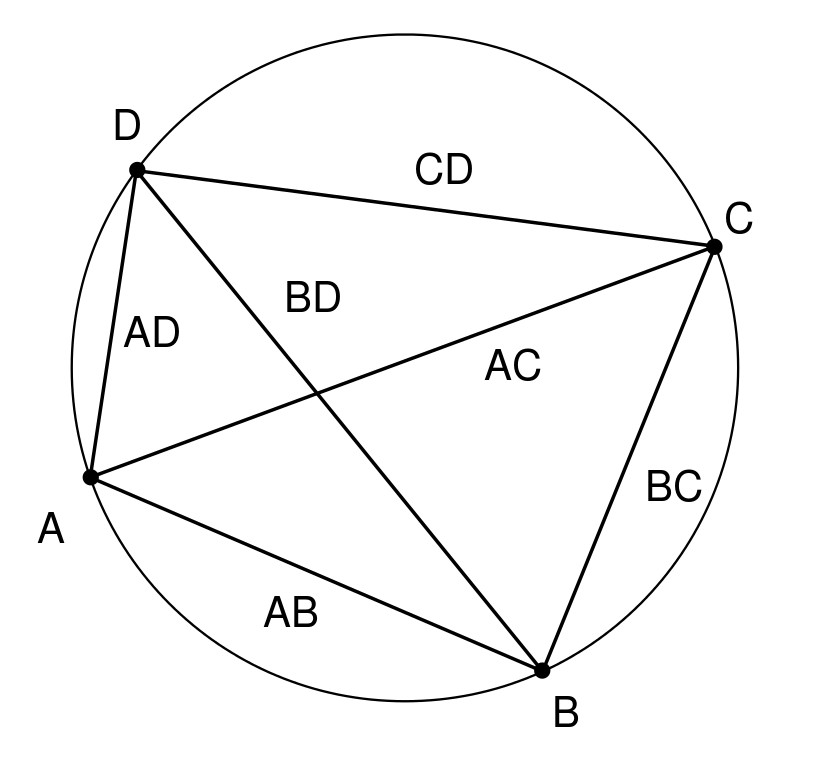
Consider a quadrilateral ABCD with all of its vertices, i.e, A, B, C, D lying on a circle, thus, forming a cyclic quadrilateral. Here, AC and BD are the diagonals of the quadrilateral, while all the other line segments (AB, BC, CD, AD) are its sides. Now, according to Ptolemy’s Theorem, the sum of the product of the opposite sides (AB × CD + BC × AD) is equal to the product of the diagonals (AC × BD).
Mathematically,
AC × BD = (AB × CD) + (BC × AD)
There are several methods by which the above relation and thus the theorem has been proven over the years. Some mathematicians use trigonometric identities to prove the relation, while others make use of complex numbers or inversive geometry. However, the simplest of all proofs (according to us) is provided by the use of similar triangles and their properties.
As with almost every mathematical proof, we start by assuming something.
For the above cyclic quadrilateral, there exists a point K on the diagonal AC, such that ∠ABK = ∠CBD.
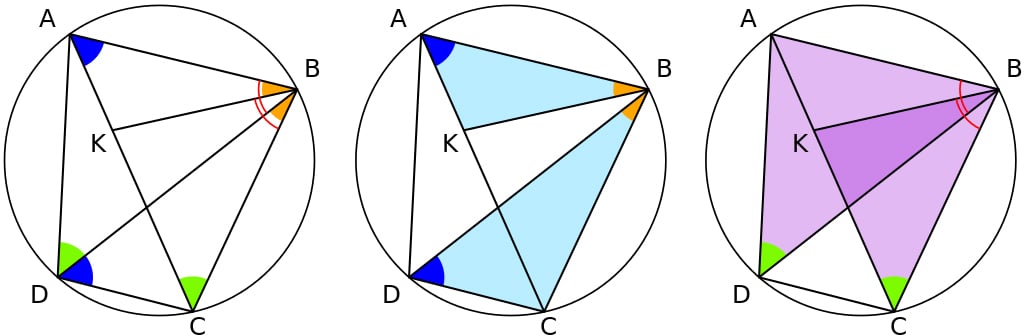
As seen in the above diagram, arc BC subtends ∠BAC & ∠BDC and according to the inscribed angle theorem, ∠BAC = ∠BDC. Similarly, arc AB subtends ∠ADB and ∠ACB, so the two angles are equal (∠ADB = ∠ACB). By the angle-angle (AA) theorem of similar triangles, △ABK is similar to △DBC and △KBC is similar to △ABD.
For similar triangles △ABK and △DBC:
Therefore, 
Likewise, for similar triangles △KBC and △ABD:
Therefore, 
Adding the above equations we have:
AK.DB + KC.BD = AB.DC + BC.AD
Here, DB and BD are the same and can be carried out as a common multiple,
(AK+ KC).BD = AB.DC + BC.AD
From the diagram, AK + KC = AC.
Therefore,
AC.BD = AB.DC + BC.AD
There it is. The product of the diagonals of a cyclic quadrilateral ABCD is equal to the sum of the product of its opposite sides, just as Ptolemy’s Theorem tells us!
Applications Of Ptolemy’s Theorem
As mentioned earlier, Ptolemy’s Theorem can be extended to cyclic pentagons and used to prove the golden ratio relation between its sides and diagonals.
For a regular cyclic pentagon ABCDE, the sides are of length ‘a’ and the diagonals are of length ‘d’.
Concentrating just on the quadrilateral ABCD and applying Ptolemy’s theorem, we get:
AC.BD = BC.AD + AB.DC
Substituting the respective length values,
d.d = a.d + a.a
d2 = a.d + a2
Dividing the above equation by a2
d2/a2 = d/a + 1
Now, let the ratio ‘d/a’ be represented by ‘r’
Therefore, r2 = r + 1
Rearranging, r2 – r – 1 = 0
Solving for r,
r = (1 ± √1 – 4(1)(-1)) / 2
r = (1 ± √5)/2
r = 1.618033…
Therefore, the ratio of a regular pentagon’s sides to its diagonals (r = d/a = 1.618033) is the golden ratio.
Similarly, to prove the Pythagorean Theorem using Ptolemy’s Theorem, imagine a rectangle ABCD inscribed inside a circle.
Applying Ptolemy’s Theorem to rectangle ABCD, we have
AD⋅BC = AB⋅DC + AC⋅DB
For any given rectangle, opposite sides are equal, as are the two diagonals. Therefore, AB = CD, AC = BD and AD = BC.
BC2 = AB2+ AC2
The above equation is nothing but the Pythagorean Theorem applied to the right-angled triangle ABC.
A Final Word
Apart from the two corollaries explained above, Ptolemy employed the theorem of cyclic quadrilaterals to construct his table of chords (a trigonometric table similar to the table of values of sine function we still use today). While not the first of its kind, Ptolemy’s table of chords provided values of trigonometric functions with an increment of 30′, whereas the first trigonometry table created by Hipparchus provided values at an increment of 7°30′.
This resulted in far more accurate interpolations and helped in calculating the positions of various planets, the sun, the moon, the rising and setting of the stars, dates of lunar and solar eclipses, etc.
The amalgamation of Ptolemy’s astronomical work manifested in the form of thirteen books, collectively known as the Almagest, which is considered one of the most influential works in the field of astronomy. His work superseded all previous astronomical works, reigned supreme for a number of years and is therefore hailed as the greatest astronomical work of antiquity.
Many of Ptolemy’s astronomical achievements wouldn’t have been possible without the use of the table of chords, which wouldn’t have been constructed if not for Ptolemy’s Theorem of cyclic quadrilaterals!