What Is The Four Color Map Theorem?

The four color map theorem is a theorem that states that you only need four colors to color all the regions of any map without the intersection or touching of the same color as itself. The theorem applies to all maps, regardless of their complexity or density of demarcations.

When it comes to the shroud of theorems present in mathematics, a few of them stand out in comparison to others. One such theorem that stands above the rest is the four color map theorem or the four color theorem.  The four color map theorem is exactly as it sounds. You only need four colors to color all the regions of any map without the intersection or touching of the same color as itself. The beauty of this theorem lies in the fact it applies to all maps, regardless of their complexity or density of demarcations. Before we get into the nuances of understanding, let’s briefly review the history of the theorem.

Recommended Video for you:

History

As far as credible sources go, the first proposal of such a conjecture was made by Francis Guthrie on October 23, 1852. The proposal occurred while trying to color the map of England, when it was noticed that only four different colors were needed. At the time, Guthrie’s brother was a student of the famous mathematician August De Morgan at the University of London.

The problem, which is so simple, proved itself to be tantalizingly difficult. In 1860, De Morgan took the problem and its proof to the United States of America. In America Benjamin Price (1809-1880) a famous mathematician and astronomer, chose to develop logical methods to investigate this conjecture. De Morgan used the fact that in a map with four regions, each touching the other three, one of them is completely enclosed by the others. Since he could not find a way of proving this, he used it as an axiom, the basis of his proof.

First Attempt At A Concrete Proof

In 1878, Arthur Cayley (1821-1895) at a meeting of the London Mathematical Society, asked whether anyone had found a solution for De Morgan’s original question, but although there had been some interest, no one had made any significant progress. Cayley took particular interest in the problem, and in 1879 published a short paper on the coloring of maps, where he explained some of the difficulties in attempting a proof and made some important contributions to the way the problem was approached. His question that, ‘if a particular map is already successfully colored with four colors, and we add another area, can we still keep the same coloring?’ began another line of inquiry that led to the application of mathematical induction to the problem.

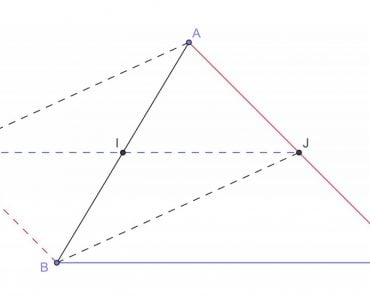
Arthur Cayley was able to show that if four colors had already been used to color a map, and a new region was added, that it was not always possible to keep the original coloring. Above, all four colors have been used on the original map, and a new region is drawn to surround it. In this case, a red area is changed to blue so that that red can be used on the new surrounding region. Cayley was able to observe that it was possible to solve a version of the problem by restricting the way the boundaries met. For example, maps, where just three countries met, have three edges meeting at a vertex. These are called ‘cubic maps,’ and the maps used in the following discussion are all cubic maps. Also, if a map can be colored with four colors, only three colors will appear on the border.

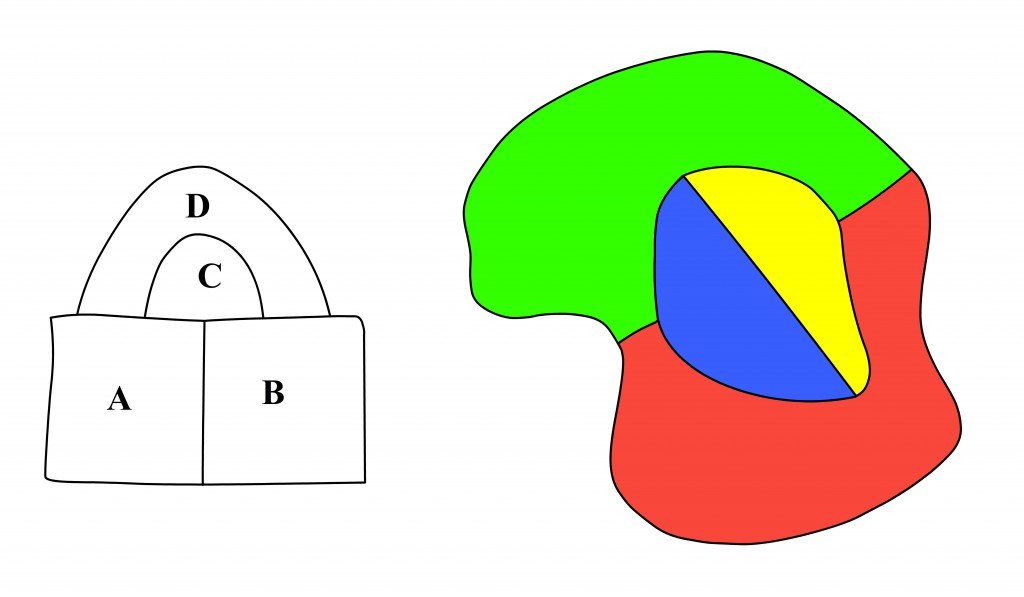
The Patch demonstration.

Imagine that at some place in a map, some countries meet at a point. Now, put a patch over the meeting point, and all the new meeting points will have three borders emanating from them. These are cubic maps, and a fourth color can be used for the central region. Upon removing the patch, we can return to the original coloring.

Understanding The Basics

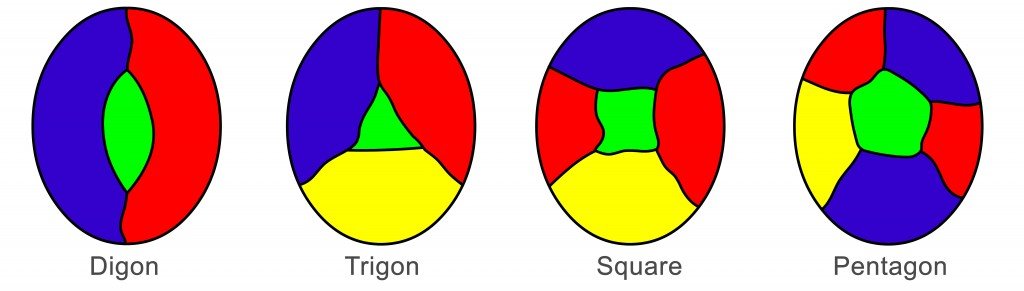
In order to work on a more concrete proof for the four-color problem, we will need to build an understanding of certain terminologies, ideas and techniques that mathematicians have developed to solve it. The first concept is “Every country has five or fewer neighbors”. Now, to understand this statement, imagine a map of an island surrounded by a sea. In the coloring of the countries of the island, we count the sea as one region. Some countries may have only two borders (a digon), some three (as in a triangle), some four (a square) and some five (a pentagon) or more.

When False Becomes True

Another way to approach proving the four color problem is to assume that it is false from the onset, and see where it leads. Suppose there is a map that needs five or more colors and the map we have picked contains the smallest number of countries present in it. The name for such a map is known as the minimal counter example or even more interestingly, minimal criminals!

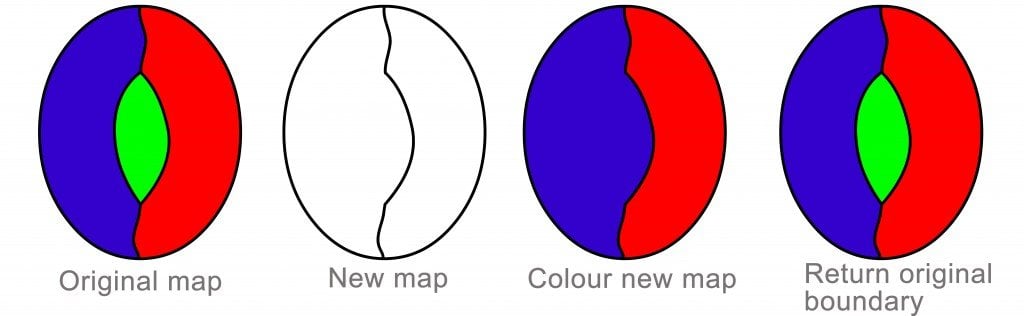
The above paragraph now implies that the minimal criminal cannot be colored with four colors. This implies that any map with countries lesser than the minimum criminal can be colored in four colors if we can prove that the minimal criminal does not exist, then that leads to some substantial progress in the proof. The first thing we can state conclusively is that a minimal criminal cannot be a digon. From the original map, if one were to take away the boundaries of the digon, we get a new map with fewer countries. The resultant map can be colored with four colors from our assumption. When we color the map, we observe that we need only two colors.

Now, if we reinstate the border we removed and recolor the map, we observe that we have only used three colors so far, and still have one color in the reserve. We have used three colors, and since there is still one more color available, this shows that our map can be colored with four colors. But this is against our assumption, so a minimal criminal cannot contain a digon. This procedure can be repeated to show that a minimal criminal cannot contain a three-sided country (a trigon), but it breaks down when we try the technique on a square, because when we replace the square, the countries next to it may be using all four colors, so the proof procedure fails. Once this has happened, it becomes obvious that it won’t work for pentagons, and so on.

There are substantial and more rigorous methods one can use to prove the four problem theorem, such as graph theory and so on, but to this day, it remains a solid and irrefutable theorem that any map can be colored with only four colors!