Table of Contents (click to expand)
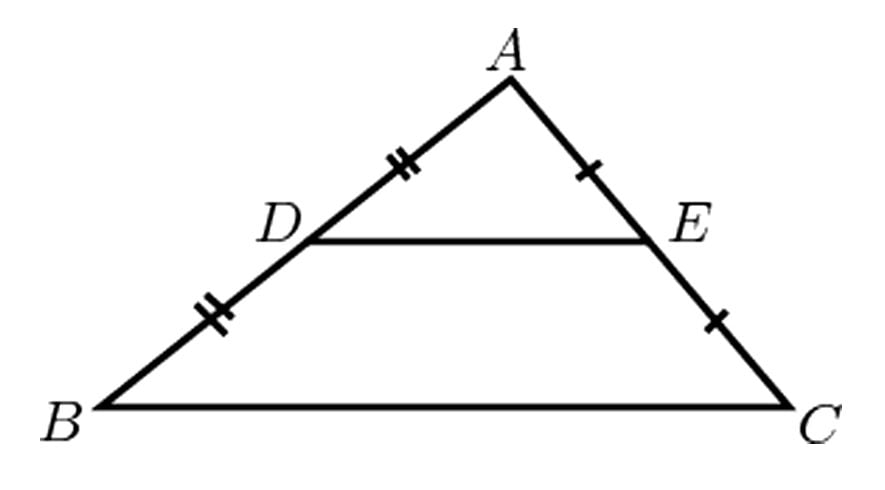
The midpoint theorem states that the line segment connecting the midpoints of two sides of a triangle is parallel to the third side and is congruent to one half of the third side. Whereas, its converse states that the line drawn through the midpoint of one side of a triangle and parallel to another side bisects the third side.
Imagine sitting in a baseball stadium and watching your favorite team play!! It was a good game, right? Baseball has one of the most uniquely shaped fields in sports, much different than the most common rectangular or circular playing fields, and it is referred to as a Baseball Diamond.
Now, someone with even a bit of mathematical knowledge might wonder how that field was made? Curiosity regarding the construction of the diamond-shaped, field according to the specified dimensions and the theorems involved in its construction, must make one feel inquisitive.
If you take a closer look towards the field or see a birds’ eye view of the field, you will notice that the diamond looks like the sector of a circle with a triangle in it (joining the endpoints of the grass line with the help of a straight line). With that image in mind, let’s explore the mathematics behind the construction of the legendary baseball diamond.

Recommended Video for you:
Midpoint Theorem
The midpoint theorem states that “For a given triangle ∆ABC, let D and E be the midpoints of AC and AB, respectively. Then the segment DE is parallel to BC and its length is one half the length of segment BC.”
Or, in simple words, it can be stated as The line segment connecting the midpoints of two sides of a triangle is parallel to the third side and is congruent to one half of the third side.
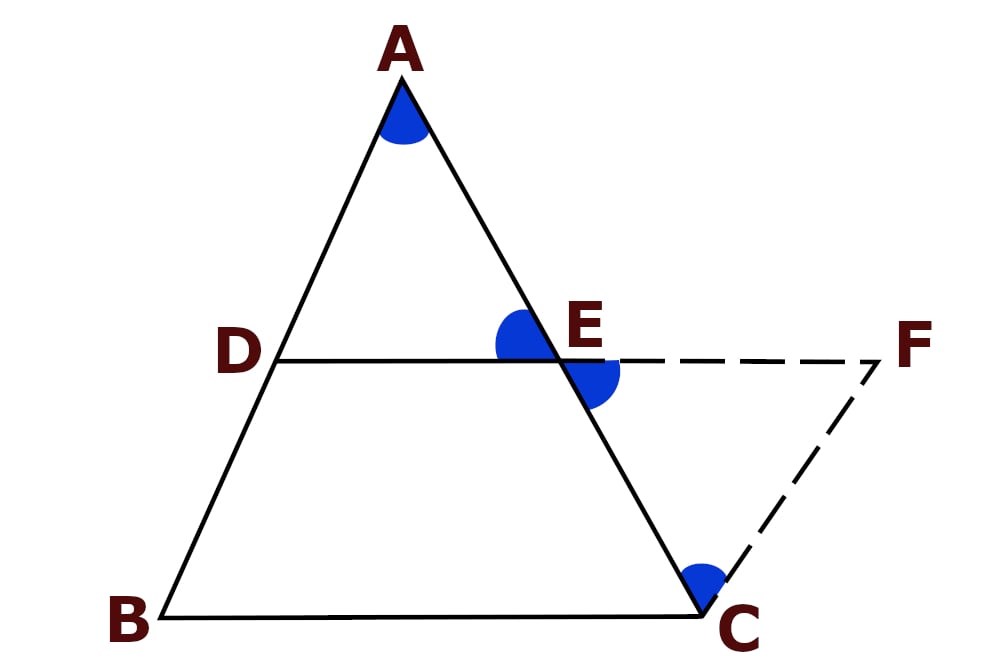
Midpoint Theorem Proof
Any theorem must have a mathematical proof for it to be valid and the midpoint theorem also has one.
To Prove- DE = (1/2) BC and DE||BC
In the above figure, extend the line segment DE to a point F in such a way that DE = EF and also joins F to point C.
In triangle ADE and ECF, we have – DE = EF (by construction), ∠ AED = ∠ CEF (since they are vertically opposite angles) and EC = AE (since E is the midpoint of AC).
According to the above results, we can say that the triangles AED and CEF are congruent. Therefore, we can say that ∠ ADE = ∠CFE (alternate interior angles), and similarly, ∠DAE = ∠FCE (alternate interior angles) and AD=CF.
Therefore, we can say that CF||AB, so CF||BD. Since opposite sides of the quadrilateral BDFC are parallel and equal, BDFC is a parallelogram, hence BC||DF, i.e., BC||DE and DE = (1/2) BC.
Hence, the midpoint theorem is proved.
This is the general textbook explanation that students tend to understand, but never question in terms of its application to real-world problems. Now, before this gets boring, we’ll shift back into baseball to make this concept more interesting and easy to understand.
Practical Understanding
To understand any theorem, it’s essential to understand its practical importance and application. So, we’re coming back to the baseball field for a practical understanding of the theorem. Below are the dimensions of a baseball field (listing only the important/relevant dimensions to prove the practical application of the midpoint theorem).
- Home to first base – 27.43 m
- Third base to home – 27.43 m
- Home to left-field foul pole – 99.06 m
- Home to right field foul pole – 99.06 m

The known distance between the two foul poles is 140.09 meters; we can now use the midpoint theorem to calculate this and find out whether the theorem is practically valid or not.
Considering the triangle formed by the two foul poles and home plate, we have two sides of the triangle, both having their length equal to 99.06 m, and the third side, i.e., the distance between the foul poles, which is 140.09 m.
The midpoints of the equal sides (from home plate to the left and right foul poles) are at a distance of 49.53 m from home and poles. Now, if you join the two midpoints with the help of a line segment, the length of the line segment is unknown, but can be easily determined using basics or trigonometry and triangle congruency.
Here we have A (home plate), B (right foul pole) and C (left foul pole). O is the perpendicular dropped from A to line segment DE.
We will consider AB = AC since in a baseball field, the distance of the two foul poles from home plate is the same. Now, we know that in the triangle AOD, we can calculate DO by –
Cosine = Base/Hypotenuse, ∠ ADO = 45 (since a baseball field is symmetrical)
Therefore, cos 45= Base/49.53, which gives us the length of the base DO, i.e., 35.02 m. Also, since the triangles ADO and AEO are congruent by RHS congruency, line segment MN = 70.04 m, which is one half of LR, hence proving the midpoint theorem!
Conclusion
If you pay attention, you will see that we are surrounded by real-world examples that can help us learn subjects in a much more unique and fun way. However, it is up to us to find them!
Mathematical theorems have their applications in various fields, but who would have thought that even their favorite sport would have applications from a subject which is a nightmare to most!