Table of Contents (click to expand)
Geographers measure elevation by drawing numerous triangles. Amongst the three sides, one is the altitude of the mountain whose elevation must be measured. This is achieved by using an advanced protractor, known as a theodolite. Even the Greeks measured elevation by “comparing the ratios of two sides of a triangle”.
According to an old legend, when the highly acclaimed Welsh surveyor and geographer Sir George Everest measured Mount Everest, then known as Peak XV, to be exactly 29,000 feet tall, his team decided to add two feet to their measurement to make it seem more believable. The cloud-piercing summit was then believed to be reposing calmly, secluded from everything else, at 29,002 feet above sea level.

Subsequently, the advent of sophisticated technologies like satellites measured the peak’s height to be 29,029 feet tall. Sir Everest’s discovery is extremely remarkable, however, considering that he made it in 1852 without the assistance of tools with which geographers are currently equipped. What’s more, his team carried out the measurements from more than 100 miles away from the peak, as Nepal’s government wouldn’t allow Britishers to enter their country. So how did they achieve this astonishing feat?
Recommended Video for you:
Trigonometry
As a child, the oldest method I can remember to determine length was to scale it with my hand. A single unit of measurement would be the distance between my thumb and the pinky when the hand was moderately stretched. To measure, say, a table, I would place my stretched hand upon it. Next, the pinky would leap forward, allowing the thumb to take its place, and the length would then measure two units. The scampering would continue until the entire length was accounted for.
Eventually, hands were replaced by rulers, but the methodology remained the same – stack one beside another until the entire length is covered. No one will deny that measuring how tall Mount Everest is with a ruler or your hand is possible, but I’m sure that everyone would agree that the process would be a bit time-consuming and cumbersome.

Yet, the method that geographers rely on isn’t far from using rulers. In fact, Sir Everest and his team implemented high-school geometry to measure the elevation of Mount Everest. Yes, that’s right, their tools were just fancier, more sophisticated sets of rulers and protractors. Trigonometry had been used by the Greeks to measure tall structures and by Victorian surveyors to measure the tallest mountains before we moved onto satellites. However, even satellites measure elevation by essentially implementing the same principle – drawing triangles.
Triangles
Geographers measure elevation by drawing numerous triangles. Amongst the three sides, one is the altitude of the mountain whose elevation must be measured. The base of a triangle is drawn between the mountain’s feet and a point, let’s say A, that is situated at a known distance from the mountain’s feet. The third side can be formed by simply connecting point A and the summit.
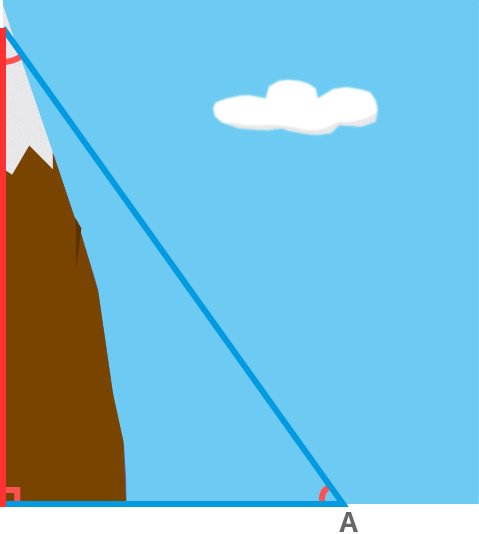
While forming the horizontal base, geographers must ensure that it is completely level to achieve accurate results. The discernment of any irregularity on Earth’s craggy surface is achieved with the help of highly delicate instruments. Next, they must measure all three angles formed within the triangle. This is achieved by using an advanced protractor, known as a theodolite. Measuring even two angles is sufficient, as the third angle can be calculated by subtracting the sum of the two known angles from 180, as the sum of all three angles bounded by a triangle is equal to 180º.
Now, behold the magic of simple trig — the knowledge of two angles and the length of one side can reveal the altitude of the mountain. Even the Greeks measured elevation by “comparing the ratios of two sides of a triangle”, which, if you’ve learned basic trig, is essentially performing the same operation.
For instance, consider a very simple example where the angle formed at point A is 60º, and we only know the distance between point A and the mountain’s base, which is, of course, the triangle’s base. For simplicity, let’s assume the triangle is a right-angled, where the base is perpendicular to the altitude. This implies that the third angle, formed at the summit is 30º (180º-[90º+60º]). Let’s also label the triangle’s sides. Starting from the altitude and going clockwise, let’s label them as X, Y and Z units.
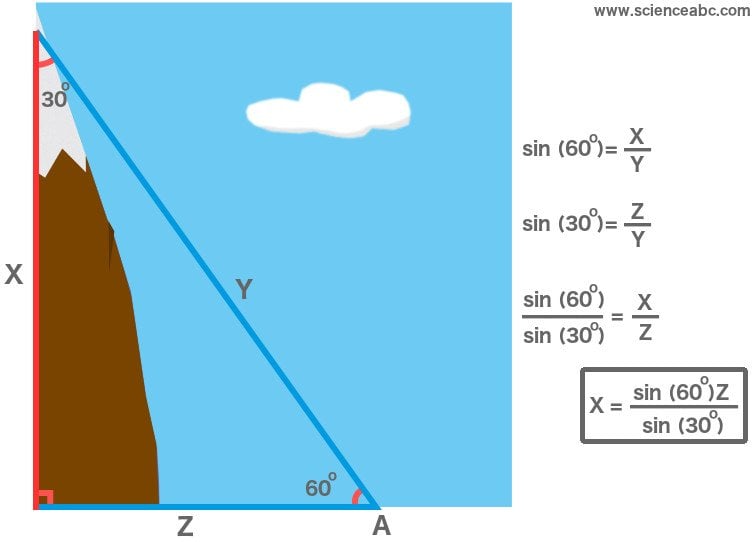
Now, Sin (60º) represents the ratio X/Y, while Sin (30º) represents the ratio Z/Y. If we divide these ratios, we observe that the two Ys cancel out and we are only left with the ratio X/Z. The values of both Sin (60º) and Sin (30º) can be learned by simply referring to a high school math textbook. Furthermore, Z is the base of the triangle, the magnitude of whose length we already know. Multiply Z with the ratios of Sines and we have the altitude – X — of the mountain.
Sir Everest drew several such triangles, all emanating from different A’s, as the measurements from one triangle could not be trusted. The team then averaged each and every altitude derived from all the triangles. This led them to arrive at no more or less than 29,000 feet, a number that is comically rumored to have been incremented to deter any suspicion.
Later, in 1999, scientists with the aid of satellites, measured Everest’s elevation to be 29, 029 feet above mean sea level. Sir Everest’s precision is nothing short of phenomenal — the true peak is just 27 feet taller than what he predicted. Only two angles and one side, that’s it!