Table of Contents (click to expand)
Quantum mechanics can be challenging to comprehend due to its foundation on postulates about wave functions that are hard to relate to. Furthermore, quantum particles do not adhere to classical laws, making it challenging to predict their behavior.
If you’ve ever read sci-fi comics, you’ve probably noticed certain buzzwords that are often used, such as “quantum mechanics,” “singularity,” “quantum decoherence,” and so on. These words tend to grab readers’ attention and create a sense of mystery around these phenomena, making readers curious about the quantum world. This contributes to the idea that quantum mechanics is difficult to understand.
Let’s try to unravel the mysteries of the quantum world because the true beauty of science lies not in the wonder of mysterious phenomena but in the persistent efforts to understand them and push the boundaries of knowledge.
Recommended Video for you:
Quantization Of Energy: Breaking Established Laws
The word ‘quantum’ in physics is not an adjective that would describe a certain entity. Instead, quantum actually comes from the word ‘quantized.’ In the 1900s, it was discovered that the energy of micro-scale systems (a collection of molecules, atoms, electrons bound to a metal, etc.) could only have certain allowed values.
Imagine throwing a tennis ball. The speed of the ball could, in principle, have any speed in the continuous range from 0 km/h to 150 km/h (realistically, based on arm strength). However, if the ball were subjected to quantum mechanical laws, then the ball would move only at certain allowed values, for example, at speeds that are multiples of 2km/h (i.e. 2, 4, 6, 8, …) or at speeds that are exponents of 3km/h (i.e. 3, 9, 27, 81,…). This would mean that there exist some forbidden speeds at which the ball cannot move. Thus, the plot of speed versus time would be discontinuous. This rather absurd phenomenon is actually true for quantum particles like electrons and protons. This is called the quantization of velocity. Since kinetic energy depends on velocity, the quantization of velocity also leads to the quantization of energy.
Ultraviolet Catastrophe: First Hint Of The Quantum World
In the late 19th century, physicists attempted to calculate the total energy emitted by an ideal blackbody. They tried to sum the energies of all the atoms making up the blackbody using the laws of classical physics. However, their calculations led to a surprising result. They found that the energy emitted by a blackbody in thermal equilibrium with its surroundings is infinite.
In simpler terms, this meant that the energy emitted by the blackbody was greater than the energy of all the stars, planets, comets, asteroids, etc., in the universe combined.
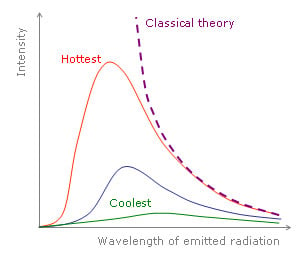
This absurd result prompted physicists to look for alternative theories. The problem was solved when Max Planck assumed that the atoms making up the blackbody emitted energy with only certain allowed values. In simple terms, this meant that the energy emitted by all the atoms was quantized. Simplifying this further, each atom could emit certain allowed energies. This simple assumption solved the problem of infinite energy, and theoretical calculations (which earlier gave absurd results) matched with practical observation.
Weird Phenomena At The Quantum Scale
What if you were told that you have a wave associated with you? Well, believe it or not, so does your car, your house, and your clothes. In fact, all physical matter in the universe has a wave nature associated with it.
Single Electron Interference
Interference is the superposition (vector addition) of waves of the same frequency traveling in the same direction.
In this experiment, a source emits electrons toward a photographic film kept some distance apart. Between the source (S) and the film (F) lies a wall (W) with two holes in it, also some distance apart. The electron emission rate is controlled so only a single electron crosses W at a time. A classical analogy would be a tennis ball thrower shooting toward a wall with two holes such that, at any time, only a single ball crosses the wall. A sheet behind the wall records the area where the ball hits.
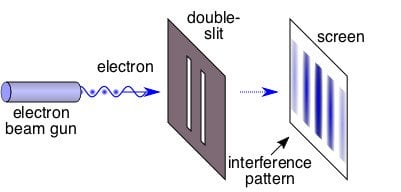
Classical theory (tennis ball) predicts that the striking pattern obtained on the sheet will be random. Extending this theory to the quantum world (single electron) would expect a random strike pattern on the photographic film (F).
However, the observations surprised physicists. The pattern obtained on F consisted of high-intensity and low-intensity areas placed a regular distance apart. This pattern is similar to an interference pattern caused by light waves. After identifying a clear pattern characteristic of waves being caused instead by particles (electrons), it was concluded that particles also have a wave-like character.

Quantum Decoherence: Destroying Observability
Continuing further with the single electron interference experiment, the apparatus was originally kept out of observation while it ran. This means that while the electrons were being emitted and hitting the film F, no observation of the process was made. After the experiment ran for a few hours, it was stopped, and the film F was retrieved. However, what if the experiment was recorded by a camera? Or observed with the naked eye?
Well, quite surprisingly, the interference pattern vanished, or rather, no pattern like the earlier one was observed. The pattern was random in this case, just like the tennis ball experiment. In other words, observation destroys interference. This isn’t the case with tennis balls, though. You may keep as many cameras and spectators present as you want, yet the pattern wouldn’t change.
This happens because, at the quantum scale, the electron is disturbed from its original path when light photons strike the electron. Thus, pure observation is lost in an attempt to make a measurement.
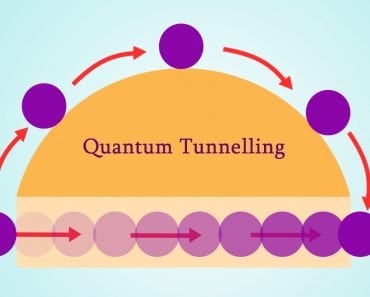
Quantum Tunnelling
Imagine a tennis ball confined to a room with infinitely high walls. It would seem impossible for the ball to cross through the walls, as it would need to be higher than the wall height to do so. Similarly, in quantum mechanics, if an electron is restricted to an infinitely deep potential well, one might think it would be trapped forever with no chance of crossing the wall.
However, quantum mechanics surprises us again. There is a finite probability that the electron will cross the potential wall when it strikes. This phenomenon is observed in real life as well. For example, two metallic conductors are soldered together in a circuit to create a joint. Despite the solder acting as a potential barrier, electrons still can cross the wall, allowing the circuit to remain closed and electricity to flow.
Conditioned Thinking With Classical Physics
Since introductory and intermediate-level physics involves classical physics, it is easier to relate to daily phenomena using these theories. However, when quantum mechanics is first introduced, it invariably starts with postulates about wave function that are difficult to relate to. Moreover, since quantum particles don’t obey classical laws, predicting their behavior becomes difficult, as does understanding the mathematical framework of QM. It’s not easy to think about operators and wave functions without trying to find a classical analogy… which simply doesn’t exist!
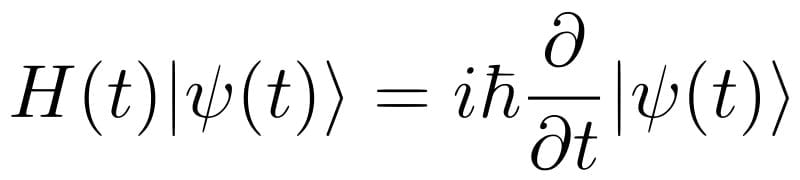
Last Updated By: Ashish Tiwari
References (click to expand)
- The Young-Feynman two-slits experiment with single ....
- The Role of Decoherence in Quantum Mechanics.
- Quantum Tunneling.
- Mathematical Fundamentals of Quantum Mechanics.
- Schlosshauer, M. (2019, October). Quantum decoherence. Physics Reports. Elsevier BV.
- Singh, C., & Marshman, E. (2015, September 23). Review of student difficulties in upper-level quantum mechanics. Physical Review Special Topics - Physics Education Research. American Physical Society (APS).