Table of Contents (click to expand)
Quantum tunneling is a phenomenon where an electron is able to phase through a barrier and move to the other side. It is a quantum phenomenon that occurs when particles move through a barrier that, according to the theories of classical physics, should be impossible to pass through.
When an object encounters a barrier, it is an intuitive understanding that the object will come to a halt or be deflected back (because the barrier can stop the object). Now, although that’s how the world of classical mechanics works, these fairly straightforward situations become slightly wonky when we descend to the quantum realm. In simple terms, quantum tunneling refers to a phenomenon where an electron is able to phase through a barrier and move to the other side. However, as Richard Feynman says, if you think you understand QM (Quantum Mechanics), you don’t understand it at all. As simple as the concept of quantum tunneling is, let’s dive straight in to understand its more complex nuances.
Recommended Video for you:
The Fundamentals
Understanding quantum tunneling in a more intuitive sense involves revisiting a few concepts of QM. The first one we will look into is the Heisenberg Uncertainty Principle. Heisenberg’s Uncertainty Principle comes into play when trying to observe particles. It states that there is a limit up to which one can determine the various parameters of a particle with a certain degree of accuracy. To understand this better, let’s take two parameters—velocity and the position of a particle—and let’s say that the particle we’re considering is an electron. Now, according to Heisenberg’s Uncertainty Principle, there is a specific limit up to which both the position and the velocity of the electron can be calculated with a certain degree of precision. If we were to focus on increasing the accuracy of either one of these parameters in more detail and focus, then the other setting would decrease in its level of precision with regards to its measurement. Thus, if you can determine the position of an electron with high accuracy, then you won’t be able to measure its velocity with great accuracy. Conversely, if you can measure the velocity of an electron to a great degree of accuracy, you will not be able to accurately determine the position of the electron.
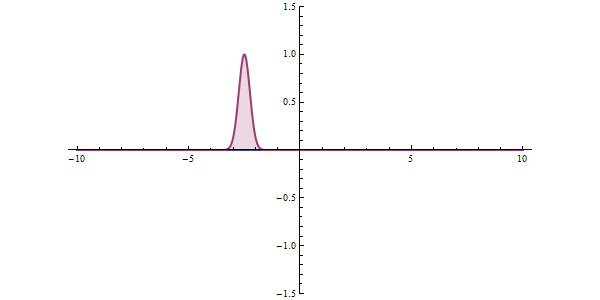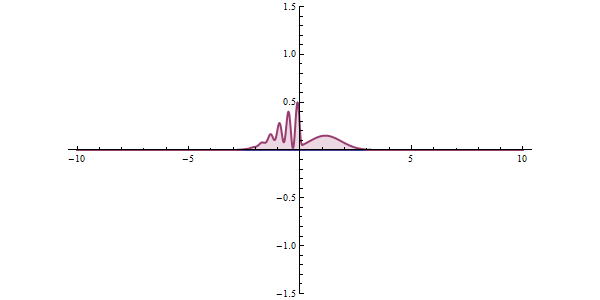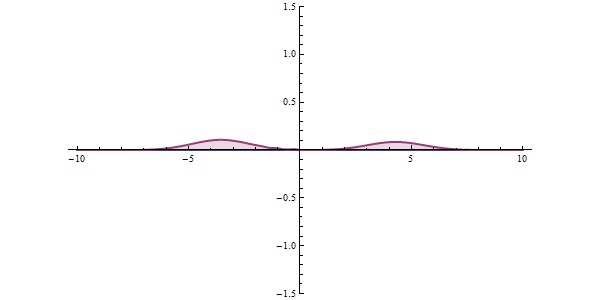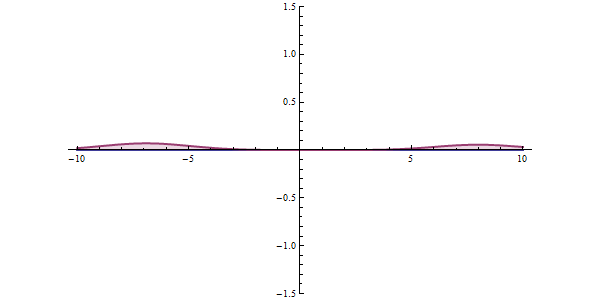
Now, another fundamental principle that must be understood is the wave-like nature of matter. The wave-like nature of a particle is a crucial aspect of one element of QM, called wave-particle duality. In the concept of wave-particle duality, every fundamental particle can be described both in terms of being a particle and a wave. This was proposed by Louis De Broglie in 1924 in his PhD thesis, which stated that if light could possess both a wave- and a particle-like nature, then an electron could also have such a dual wave-particle nature. It was through De Broglie’s relationship that he proposed in his PhD that we were able to establish the wave nature of matter. The relationship is as follows:
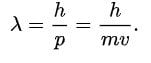Here, lambda represents the wavelength of the particle, and ‘p’ represents the momentum of the particle. The significance of the de Broglie relationship is that it establishes a foundation for the fact that matter can behave like a wave. The Davisson-Germer experiment proved the wave nature of matter beyond doubt based on the diffraction of electrons through a crystal.
Later on, the wave nature of matter was seamlessly integrated into Heisenberg’s Uncertainty Principle. The Uncertainty Principle states that for an electron or any other particle, both the momentum and position cannot be known accurately at the same time. There is always some uncertainty with either the position ‘delta x’ or with the momentum, ‘delta p’. Heisenberg’s Uncertainty equation is:
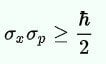Imagine that you measure the momentum of a particle accurately, such that ‘delta p’ is zero. To satisfy the equation above, the uncertainty in the position of the particle, ‘delta x’ must be infinite. From de Broglie’s equation, we know that a particle with a definite momentum has a particular wavelength ‘Lambda’. A definite wavelength extends all over space to infinity. According to Born’s Probability Interpretation, this means that the particle is not localized in space, so the uncertainty of position becomes infinite. In real life, however, the wavelengths have a finite boundary and are not infinite, so both the position and momentum uncertainties have limited value. De Broglie’s equation and Heisenberg’s Uncertainty Principle from that point on became two peas in a pod.
Bringing It Together
The quantum tunneling effect is a quantum phenomenon that occurs when particles move through a barrier that, according to the theories of classical physics, should be impossible to pass through. The barrier may be a physically impassable medium, such as an insulator or a vacuum, or a region of high potential energy. Upon encountering a barrier, a quantum wave will not end abruptly; rather, its amplitude will decrease exponentially. This drop in amplitude corresponds to a drop in the probability of finding a particle further into the barrier. If the barrier is thin enough, then the amplitude may be non-zero on the other side. This would imply that there is a finite probability that some of the particles will tunnel through the barrier. The tunneling current is defined as the ratio of the current density emerging from the barrier divided by the current density incident on the barrier. If this transmission coefficient across the barrier is a non-zero value, then there exists a finite possibility that the particle can phase through the barrier.
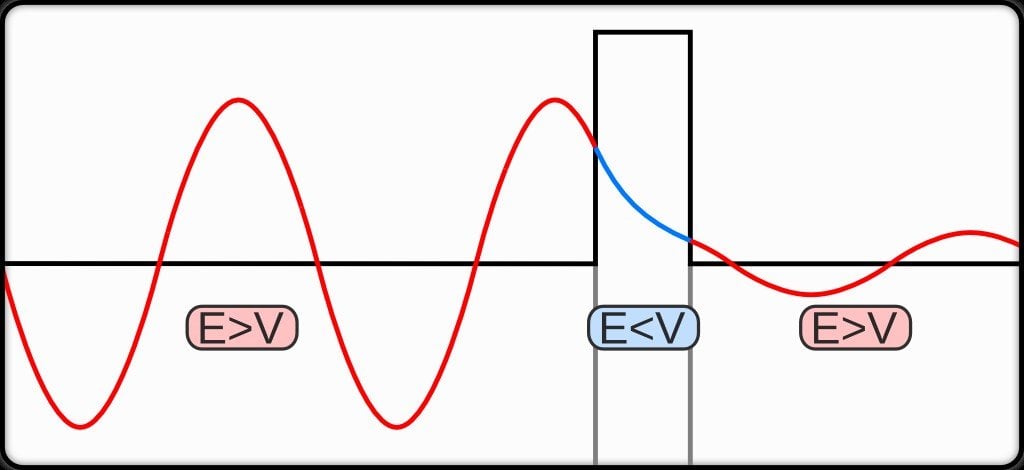
Its apparent ability to jump gaps exemplifies one of the consequences of light having a wave-like aspect. For instance, light penetrating through a block of glass at a shallow angle is effectively trapped within the glass by the barrier of air at the far side, unless a second glass block is placed close to it (but not touching). Due to the spread-out nature of the wave, some of it penetrates the air barrier and, if it encounters more glass beyond, it can continue, thus apparently jumping the air gap and escaping its prison. A similar thing happens at the sub-atomic scale, when alpha particles try to escape from unstable nuclei during radioactive decay. The particles are effectively held in the nucleus by the nuclear forces and, in principle, should not be able to escape. However, escape they do, thanks to quantum tunneling and the uncertainty principle!
