Table of Contents (click to expand)
The solution to the brachistochrone problem, as proposed by Johann Bernoulli using Fermat’s principle of light during refraction.
What do you think is the fastest path to get down a hill? We all know that a straight line is the shortest path, but is the shortest path always the fastest?
In our world, gravity is a major force that controls mechanics, and a lot of our problems are posed around it. In many video games, when shooting a far distance, we have to take into consideration the descent of the bullet due to gravity. Today’s question is, what’s the shortest time an object takes to roll or slide down from one point to another below it, but not directly below it.
There can be many different paths created between these two points. Our goal is to find the path that will take the shortest time when influenced by gravity.
Recommended Video for you:
The Brachistochrone Problem
This problem is famously known as the Brachistochrone problem, which breaks down to Brakhistos (Greek for shortest) and Kronos (Greek for time), clearly translating to the “shortest time” problem.
It was originally a challenge posed by one of the Bernoulli brothers, Johann Bernoulli, in 1696. It was an open challenge to the mathematicians of the world at that time. More importantly, it was a chance for Johann Bernoulli to show the world what a great mathematician he was. He believed that he was the best mathematician of the era, so he wanted people to know that he was better than his brother, Leibniz, and Isaac Newton, who was rather old at the time and had retired from being a mathematician.
In fact, Newton did take up the challenge, even though he was displeased to be challenged by someone he considered beneath him. That being said, Newton basically considered everyone beneath him.
So, Isaac Newton solved the problem in a single night and sent it anonymously to be published. Bernoulli later claimed that he knew that the solution was from Newton by saying “I recognize the lion by its claw”. Although Newton did solve the problem, Bernoulli’s solution was unique, clever, and surprisingly simple. This was probably why he wanted to challenge mathematicians like Newton in the first place. Now, let’s move away from the hot gossip of the 17th century and try to understand this problem in more detail.
Galileo thought of the question long before Bernoulli placed it as a challenge; he believed that the answer was the arc of a circle.
If the path were a straight line (Path 1), the ball falling is accelerated by gravity slower than when it is falling directly. Furthermore, if the path was falling vertically, and then traveling horizontally (Path 2), then the ball reaches high velocity at the beginning, but must continue its journey with the same velocity.
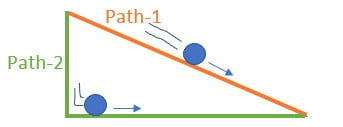
Thus, we need a path that balances being short like the straight line, as well as the high velocity of path 2.
Galileo was definitely going in the right direction when he gave the path some curvature, but he was wrong in his answer. Although the path is curved, it is not the arc of a circle that is the fastest.
Let’s talk a bit more about circles. We see them in everything, starting from a pizza to your Uber driver’s map to a satellite orbiting around the earth. Circles are most well known for rolling, although other shapes can roll on different surfaces; only circles can roll smoothly on straight paths. If you mark a point on the circumference of a circle and let the circle roll, the path followed by that point is known as a cycloid. The answer to our big question today is – a Cycloid!
Bernoulli’s Solution
Bernoulli thought of a great way to solve this problem—using the principles of light!
Fermat’s principle, also known as the principle of least time, states that the path taken by a ray between two given points is the path that can be traversed in the least time. Since our problem here requires exactly this, Bernoulli decided to create an analog of the particle-gravity system in terms of light.
Refraction Of Light And Snell’s Law
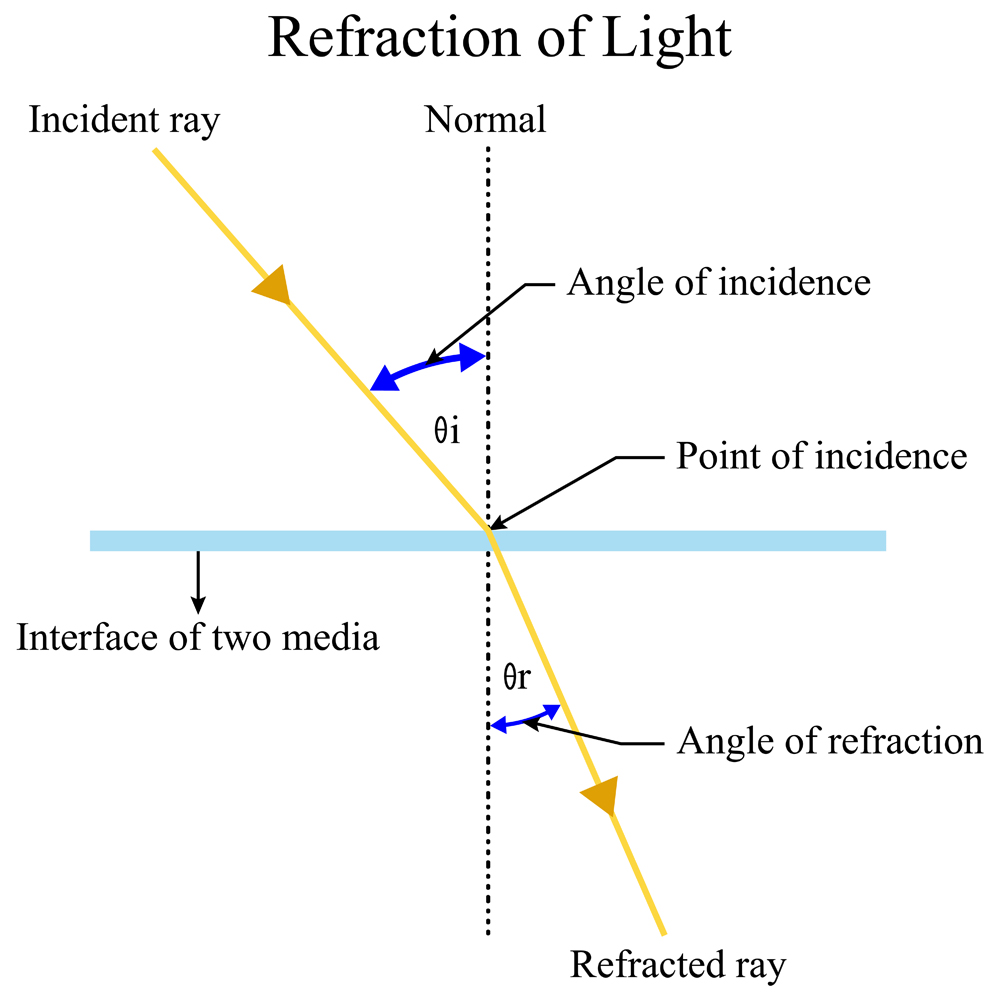
Refraction is the bending of light when it travels from one transparent medium to another. It is the principle that governs lenses, magnifying glasses, rainbows, and even our eyes.
Different transparent media, like air, glass and water have different refractive indices characteristic to them. Light refracts whenever it travels at an angle into a substance with a different refractive index. The change in direction is caused by a change in the speed of the light wave. For example, when light moves from air to water, it slows down, causing it to continue to travel at a different angle or direction
Snell’s law is given by the relationship between the path taken by light when it crosses the surface separating two different substances in contact, and the speed of light in each substance.
In the figure, v1 and v2 represent the speed of light in the two media. 
are the angles of incidence and refraction that the ray makes with the normal (perpendicular) line at the boundary. Snell’s law states
For the falling particle, due to conservation of energy, the distance from the top is directly proportional to the square root of velocity.
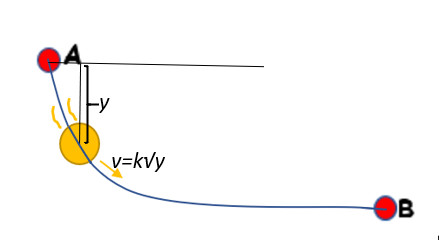
Analogous to a falling particle, Bernoulli took light traveling through media of different indices of refraction. This meant that the light would move at different speeds as it traveled along the path. And he ordered the system of media such that light would move with increasing speed, proportional to the root of the distance from the top as it ‘fell’ through, just like the particle.
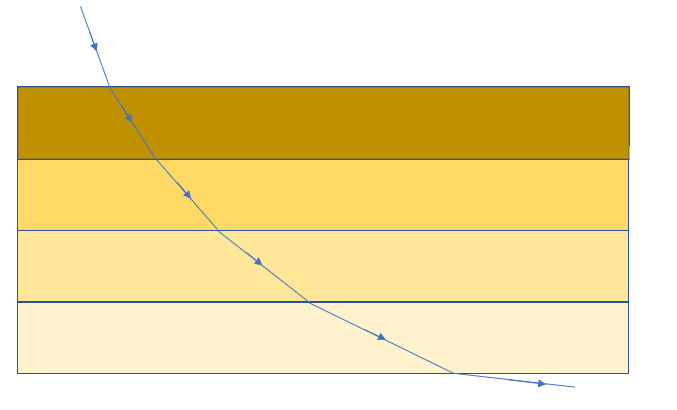
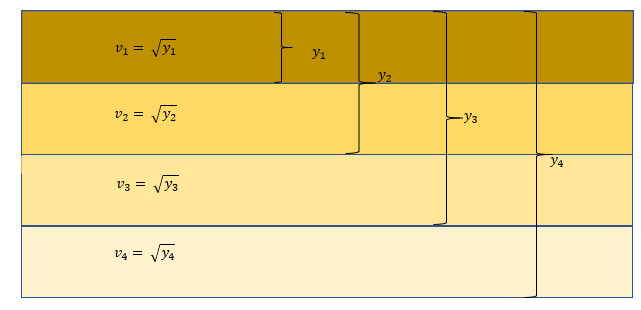
Since our classical gravity-particle system is continuous, we must understand this problem as a simplified case of a system with continuous change in media. Something more like the following image.
So, in this model, light follows Snell’s law at each interface and follows the least time principle throughout. That means, for a continuous system, the light must obey Snell’s law at every point on the path. Thus, if we figure out the path taken by light in this system, it will be the same as the path of least time taken by the particle.
The equation satisfying this condition is the equation of a cycloid. That is 
at every point on the line.
Therefore, the cycloid is the fastest path possible and is the solution to the brachistochrone problem.
The red line in the following GIF shows a cycloid. Watch how it carries the particle faster than both the other paths.
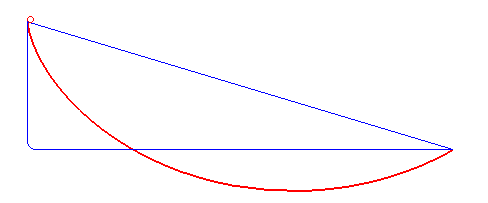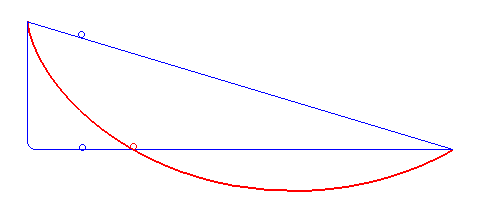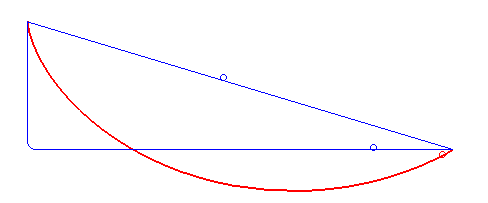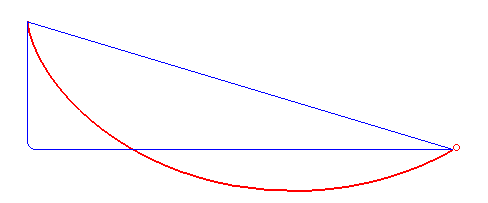
It is surprising that this particular curve, which is a cycloid, is the fastest path. It’s not a straight line, which is the shortest, nor a cliff-like path that brings maximum velocity really fast. However, here is something mind-blowing, the brachistochrone curve is also known as the tautochrone curve. This means that from whichever point on the curve you release the particle, they will reach the end at the same time!
WHAAAATT????
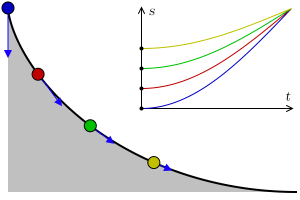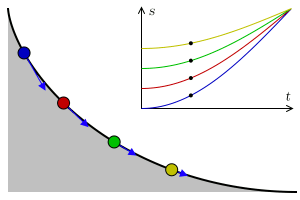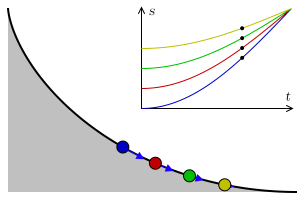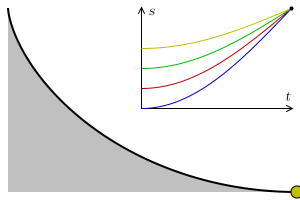
This solution is one of the most elegant things in all of physics. The idea of using light to understand something as simple as a falling object is fascinating and proves to be incredibly useful. Bernoulli’s great idea really did prove himself to be a legend among 17th-century mathematicians.
