Table of Contents (click to expand)
Every single person in the world should know the name Albert Einstein. And even if you’ve only dabbled in the achievements of Einstein, you likely know about relativity. There are two case constructs for relativity, one being the general theory of relativity and the other being the special theory of relativity. What if I told you that the math that acts as the foundation of the special theory of relativity can be easily understood – yes, even by you! To begin this journey of understanding, let’s first take a visual and geometric approach to how the Lorentz transformation came about.
Recommended Video for you:
Geometric Approach

Let’s consider a case where a man is standing stationary on the surface of the earth. Above him, his friend is traveling in a rocket. Let’s assume the speed at which his friend travels is v. Now, the hiccup we encounter when we consider relativity is that we must consider two frames of reference. For the man on Earth, his friend is traveling relative to him, whereas from the perspective of the floating friend, he is stationary while the man on Earth is moving away from him.
This poses a unique challenge, because in the Newtonian method, we only consider one frame of reference. Since both observers are right, from their given perspective, the only solution is to work around the problem in such a way that we merge them and include both frames of reference in our calculations. This can be done using a beautiful mathematical concept known as the Minkowski diagram or spacetime diagram.
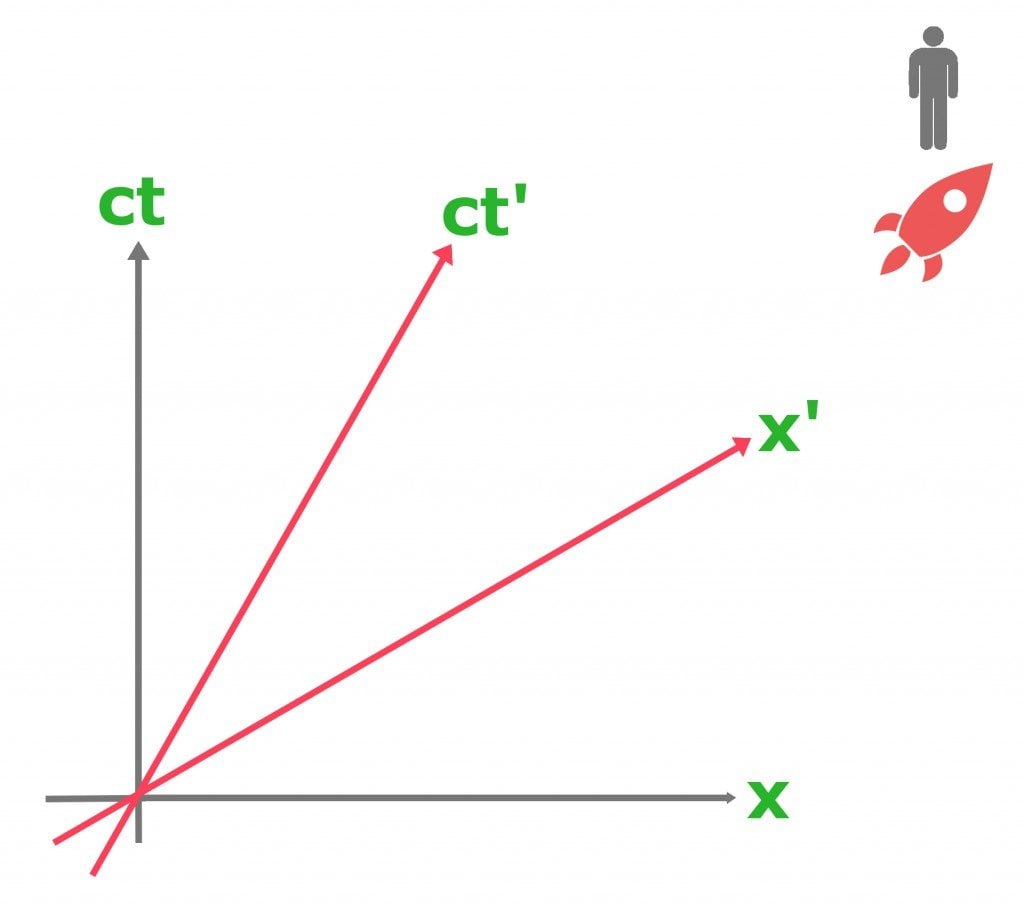
The Minkowski diagram, as seen above, takes both observers into consideration. The red axis acts as the frame of reference for the friend in the rocket, while the grey axis acts as the frame of reference for the man. This is different than the Newtonian description of motion, which only takes one frame of reference into consideration. The Minkowski diagram clearly shows that space and time have unique properties for different users, and the coordinates for a moving observer translate differently. Now, what do both axes denote? The x-axis represents distance in space, and the ct axis denotes the distance traveled by light in a unit of time. Together, this forms what is known as the space-time continuum.
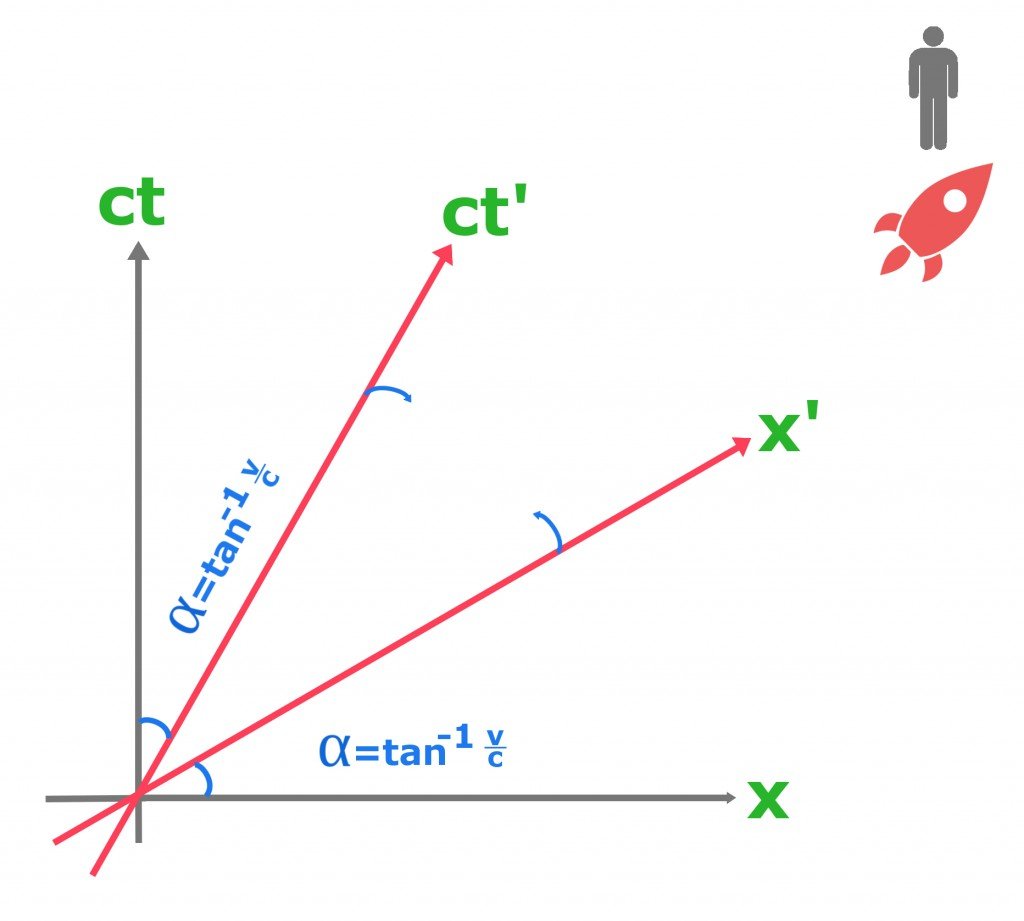
In the graph above, you will notice that the man and his friend’s graph are skewed at an angle. This angle that skews both the respective coordinates is known as the relativity of simultaneity. Although the term may sound complex, the way it is obtained is quite simple. To obtain the relativity of simultaneity, we divide the relative velocity of the friend with the speed of light and take an inverse tangent of the fraction. The equation is written as:
Tan-1(v/c)
When we look at the above equation, we notice that the more the speed of the friend increases, tending towards the speed of light, the narrower his graph coordinates become. Now, to answer the million-dollar question… If we have the coordinates for both observers, how do we mark the coordinates for the same event for two different frames of reference in spacetime? This can be easily done by first drawing perpendicular lines from the event to the x-axis and ct-axis (light years) from the man’s frame of reference, giving the x and ct coordinates. After this is done for the friend, we draw lines parallel lines to his respective axis. Where these lines intersect will be x’ and ct’.
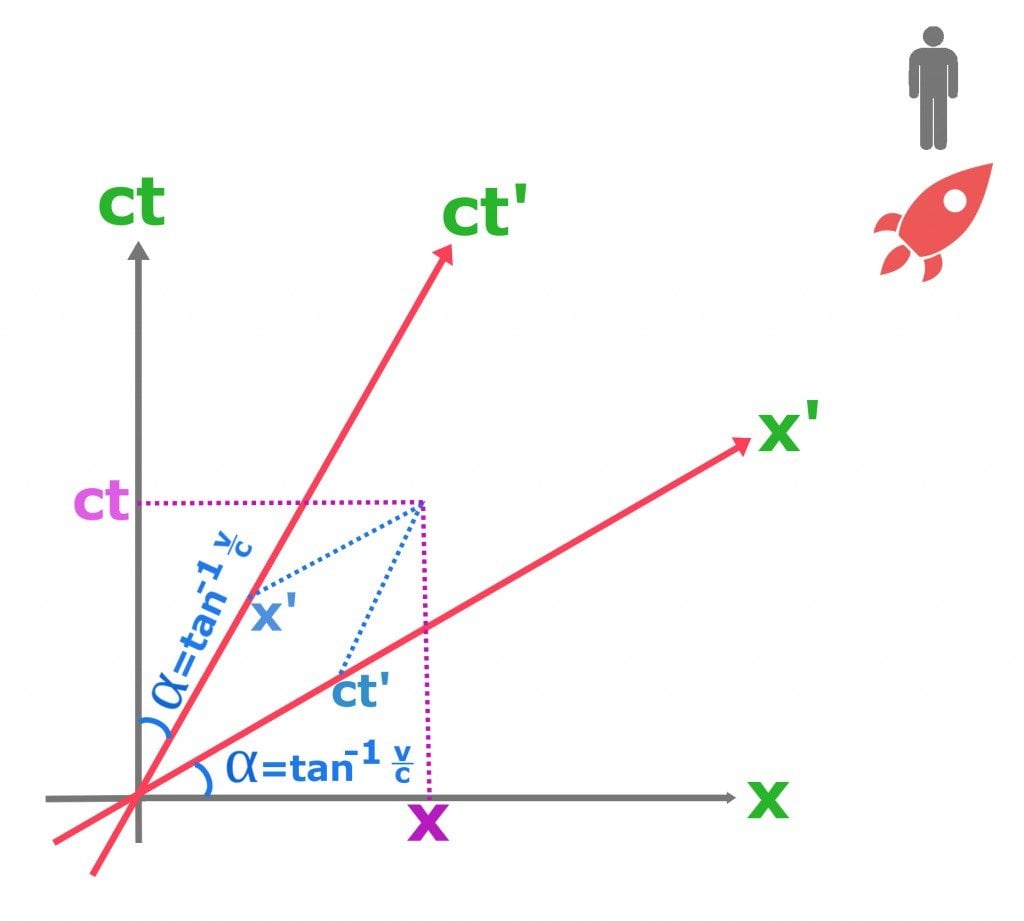
All that we did was take a geometric and visual approach, but the Lorentz transformation would help us find the friends’ coordinates much more easily using a few beautiful and intuitive algebraic expressions.
Algebraic Approach
The Lorentz transformation takes a very straightforward approach; it converts one set of coordinates from one reference frame to another. In this, let’s try converting (x, ct) to (x’, ct’). For conversion, we will need to know one crucial factor – the Lorentz Factor. The Lorentz factor is derived from the following formula:
The above equation can also be written as: ![]()
![]()
![]()
![]()
![]()
Here, beta is the ratio between the relative velocity of the observer and the speed of light. The resulting equations are known as the Lorentz boost.
![]()
![]()
The above equations not only serve as the mathematical framework for the working of the special theory of relativity, but it also played an integral part (no pun intended) in the ground-breaking solution to the twin paradox question!