Table of Contents (click to expand)
Prime numbers are extremely important in nature, popular culture and the internet. In nature, prime numbers are used by insects to ensure their survival. In popular culture, prime numbers have inspired writers, singers and other artists. In the internet, prime numbers are used to protect data and to enable online monetary transactions.
Recommended Video for you:
What Are Prime Numbers?
A whole number, which is greater than 1, and which has only 2 factors – 1 and itself, is called a prime numbers. Another way of saying it is that a prime number is defined as a whole number which has only 2 factors – 1 and itself. Some examples of prime numbers are 2, 13, 53, 71 etc.
Why Are Prime Numbers Important?
From cyber security to movies, prime numbers have made their mark in every aspect of life. Chances are that you’re using prime numbers right now, but you just don’t know it yet! In this article, we have included some of the amazing ways in which prime numbers impact our lives, and why mathematicians are still fascinated by them.
Prime Numbers Keep Your Money Safe
Did you know that the security of many encryption algorithms is based on a single important fact? These security measures have everything to do with prime numbers. Mathematicians say that it is very easy to multiply two large prime numbers and get a certain result, but it is extremely computer-intensive to do the reverse of that process. When you have a number that is the product of two primes, finding the two prime numbers is very hard. This problem is called prime factorization and finding an algorithm that does this quickly is one of the biggest unsolved problems of computer science.
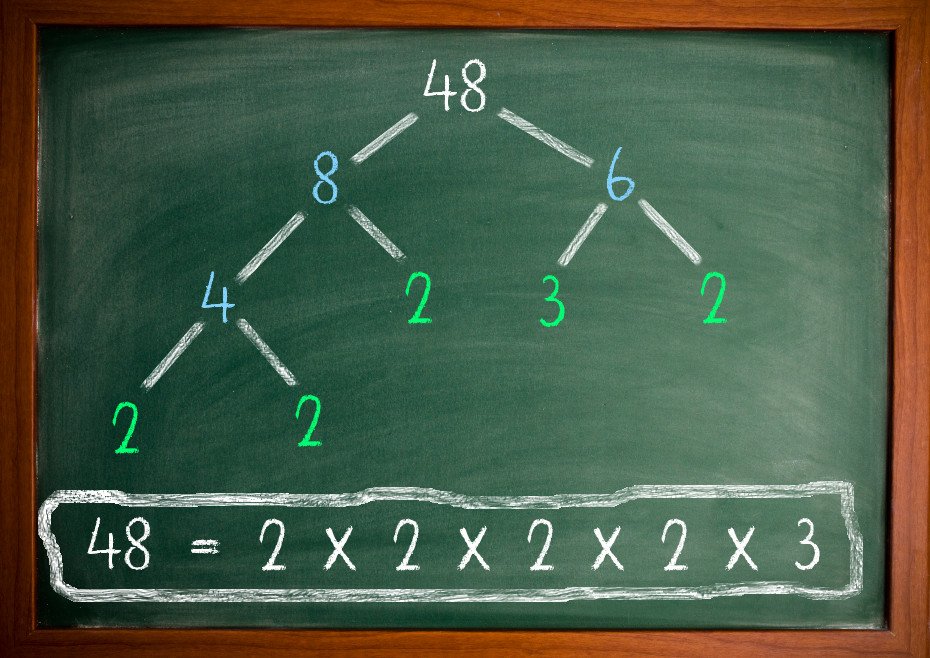
So, if passwords or security numbers are made to be long and complex, and the product of two prime numbers, it could take the fastest computer in the world decades to decode the information behind it. This gives online security firms the time they need to protect your data and apprehend the criminals. Encryption is also the life blood behind all sorts of online monetary transactions. To put it briefly, prime numbers protect your money and information from being stolen.

Prime Numbers In Nature
One of the amazing things about mathematics is how its presence can be felt in nature. You find it in the structure of a beehive, in the scales of a pineapple, or even the petals of a rose.

Prime numbers also have an amazing presence in nature. According to scientific research, it was found that the cicada insects use prime numbers to come out of their burrows and lay eggs. Cicadas only leave their burrows in intervals of 7, 13 or 17 years. It has been theorized that they use prime numbers so that predators cannot evolve accordingly and prey on them. In other words, these insects use prime numbers to ensure their survival. How incredible is that!
Prime Numbers In Popular Culture
We already know that prime numbers fascinate mathematicians and scientists. However, it has also inspired writers, singers and other artists. The science fiction and astronomy legend, Carl Sagan, wrote a book titled Contact about using prime numbers to communicate with aliens. The Academy Award winning film, A Beautiful Mind, also makes extensive use of prime numbers while telling the story of the gifted economist John Nash. These books and movies prove that prime numbers are a source of inspiration to people outside the realm of science and mathematics.
Prime Numbers In Candy Crush
Mathematical theories might sound boring, but you can’t even begin to imagine how important they are. Many ground-breaking scientific discoveries have been fueled by these theories. Even Candy Crush, the popular gaming app, is based on certain theories and principles of mathematics.

The majority of these theories wouldn’t exist without the use of prime numbers. That’s right, theories, such as the number theory, would never have seen the light of day without the help of prime numbers. So, every time you hit a combo on Candy Crush, remember to say a little thank you to prime numbers (or not, it’s up to you).
Prime Numbers Are Practically Everywhere!
Apart from the number 1, every other integer is either a prime, or consists of prime numbers. 1 was once considered to be the smallest prime number, but currently, 1 is neither a prime nor a composite number. Let’s take a random number, 26. If we break 26 down to its Lowest Common Multiple (LCM) we get 2*13, both of which are prime numbers. So, no matter what number you use, you are using a combination of primes. If you think about it, this means that you are always using prime numbers. Interesting, right?

Prime numbers carry within themselves an incredible potential and are regularly used for amazing projects. By learning about these numbers, we can educate ourselves about the world and countless technological advancements. With that in mind, next time you teach prime numbers to children, how about mentioning a few of these startling facts? Who knows, they might even unravel new mysteries of prime numbers that were never known before!
References (click to expand)
- Richie Khandelwal, Sahil Sahni - Patterns In Nature - CiteSeerX
- The beauty, mystery, and utility of prime numbers - www.math.unl.edu
- Mathematics for Computer Science - www.seas.harvard.edu
- The Poetry of Prime Numbers - www2.math.uconn.edu
- Prime and Composite Numbers - sites.csn.edu:80
- How many primes are there?. The PrimePages
- Free Printable Math Worksheets for Kids - Logic Roots. logicroots.com













