What Is The Three-Body Problem And Why Is It Hard To Solve?

The three body problem is concerned with finding the equations of motion of three gravitating bodies influencing each other. It hard to solve because of mathemtical complexity.

The branch of science that describes the natural world around us is Physics. To be as close as possible to objective reality (i.e., to only rely on what can be described with the greatest accuracy without any personal bias of the scientist), physics relies on mathematics as its core working instrument. Thus, advances in mathematics often help advance theoretical physics, which can then be verified by practical implementation. However, if the mathematics involved becomes too complex to solve, the potential advancement in physics is also affected.

Gravitational mechanics (the motion of objects due to gravity) is one of the oldest branches of physics that relies heavily on mathematics. One such problem in gravitation is the Three-Body Problem.

Recommended Video for you:

The Problem Statement

Newton’s theory of gravity explains with reasonably high accuracy the interaction between two gravitational sources. But since the real world consists of systems with more than two bodies (for example, the solar system), an equation for more than two bodies is required.

The Three-Body Problem in physics is concerned with the evolution (change over time) of a closed system (no external forces present) with three gravitational sources (three planets, three stars, or a combination thereof). The aim is to arrive at a solution that would give the value of position and momentum of the three bodies at any instant of time.

Type Of Solution Needed

The aim is to arrive at an equation (or a set of equations) that will specify the position and momentum of each body in the system at any time, using the Newtonian theory of gravitation.

These are the requirements for the solution to be feasible:

• The solution must be general, i.e. work for all possible starting configurations of the three bodies. More specifically, a solution in the form an equation (or a set of equations) is required that would give the position and momentum of all three bodies at any later time by just plugging in the value of time.
• For example, the equation y(t) = u t + 0.5 a t² is a general solution for y, where the answer can be calculated by just plugging in the value of t. The equation will be valid for any value of u and a (initial conditions).
• The solution must be closed form. A closed form solution is an expression where the solution could be obtained using a finite number of mathematical operations (+, -, , , ,  etc.) between the variables.
• For example, the equation y = mx + c is a closed form solution because a single multiplication and a single addition are used to express y. Similarly, the equation, y = e^x + is a closed form expression because there is one exponentiation, one addition and one square rooting. However, the expression, y = 1 + x + x² + x³ + …… is not a closed form solution because there are an infinite number of additions required to express y.

If a solution does not possess the mentioned attributes, that solution is discarded because:

• Lack of a general solution means that for each and every unique starting configuration, a new equation must be derived. Since there could be an infinite number of starting positions for three bodies, an infinite number of solutions would have to be derived.
• Lack of a closed form solution means that infinitely many terms must be computed, without any indication of when to stop. Thus, the accuracy cannot be determined (since there’s no end-point) and the computing power used would be enormous.

Mathematical Dead-End And Physical Interpretation

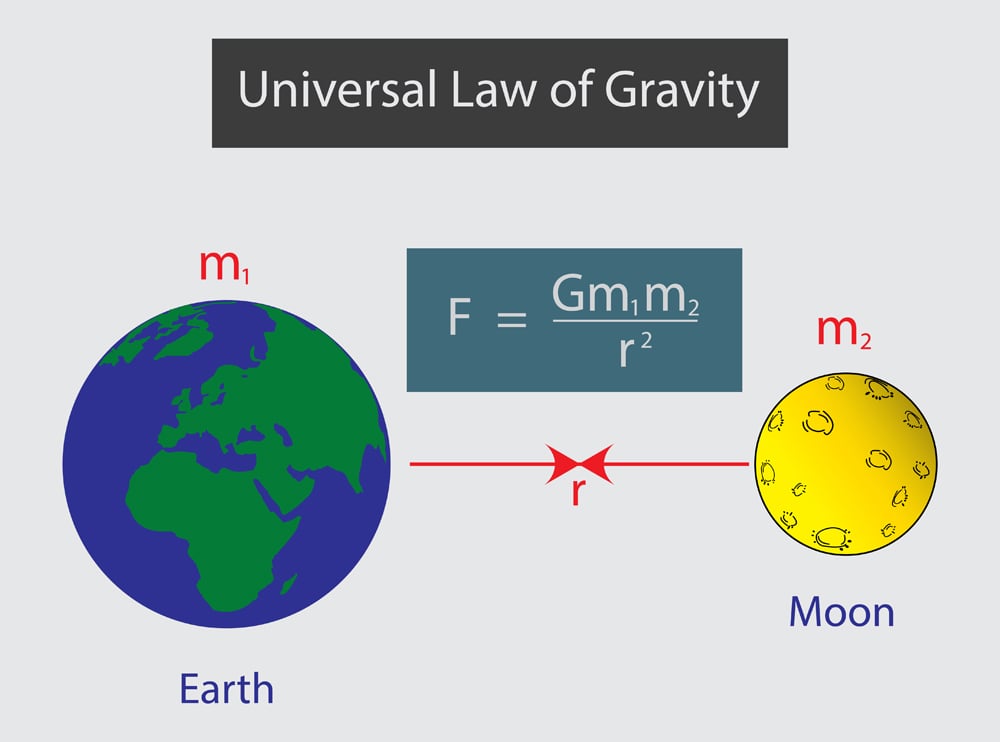
According to Newton, the force of attraction between two bodies, separated by distance r, due to gravitation is given by:

    where,

m_a, m_b = masses of bodies a and b, respectively,

= unit vector (vector of length 1) along the line joining the centers of the two bodies.

Let three masses, m_a, m_b and m_c, be placed in space in any arbitrary (random) configuration. Let the distances between the each of three bodies be r_ab, r_ac and r_bc, respectively. We wish to find the positions r_a, r_b and r_c and momenta p_a, p_b and p_c , respectively, for the three masses at any instant of time t.

Each mass is affected by the gravitational attraction due to the other two. This can be expressed mathematically as:

• Force experienced by m_a due to m_b and m_c:     
• Force experienced by m_b due to m_a and m_c:     
• Force experienced by m_c due to m_a and m_a:     

where , and are the accelerations of masses a, b and c, respectively.

The above equations are a system of differential equations, which is actually Newton’s 2^nd law applied to gravitation (gravitational force is equal to the rate of change of momentum).

Since the three masses affect each other, the above is a coupled system of equations. The energy of the system is given by the following system of partial differential equations:

where,

H = Total Energy of the system (kinetic + potential)

p_i = momentum of each mass

r_i = position of each mass

Equation (i) conveys that the change of position with time (i.e., velocity) is equal to the ratio of change of energy with change in momentum (velocity = change in total energy  change in momentum)

Equation (ii) conveys that the change of momentum with time (i.e., force) is equal to the ratio of change of energy with change in position (force = change in total energy  displacement of mass)

This is where we run into a problem.

The above system of equations is non-integrable, so it is impossible to find a general closed form solution that would predict the position and momentum at any instant of time indefinitely into the future (or the past).

Physically, this is because the motion of each body depends on the motion of the other two, and the center of mass of the system constantly shifts position. Since it is impossible to measure with complete accuracy the initial position and momentum of the bodies (accuracy maybe 99.99%, but not 100.00%), there always exists a minute uncertainty (0.01% or more or less) in the measurement of initial conditions. Since the final state depends on the initial conditions, any uncertainty in the final state gets multiplied in this system as it evolves from the initial to the final state. The longer the duration, the greater the uncertainty in the final state. If sufficient time has passed, the actual final state may be totally different from the theoretically computed state.

(Check this out if you want a rigorous mathematical study of non-integrability)

Implications Of Non-Integrability And Alternate Solutions

This critical dependence of the final state on the initial conditions makes the system chaotic. For example, even a 1mm error in measurement of the initial condition leads to a huge increase in uncertainty of the final state after millions of years. Thus, the objective of finding an expression that would give the position and momentum indefinitely into the future inevitably fails.

But wait, you might now be wondering how NASA makes predictions about comets passing by Earth hundreds of years into the future, or the widely accepted future state of the solar system thousands or millions of years into the future.

The answer is Numerical Analysis. Approximate solutions are computed (a numerical value is assigned) at each instant of time. For example, if the state of the system is required to be computed at t=50 seconds, then successive solutions are computed from t=0, 1, 2, 3, …… 50. For each instant of time, there is a numerical value associated with the position and momentum, and that value is used to calculate the solution at the next time step.