Table of Contents (click to expand)
Newton’s theory of gravity is not entirely accurate. Einstein’s theory of General Relativity explains that gravity is not a force that pulls, but rather an effect of the curvature of space-time.
Gravity is one of the four fundamental forces that constitute the Universe. I’m sure that everyone is familiar with the fable about the minor accident that led Newton to the dramatic discovery of gravity. While reposing under a tree, an apple fell on his head, and Newton, believed to be thinking about the forces of nature under that very tree, had an epiphany. What followed was a preposterous claim; he concluded that the same force that pulled the apple down from the tree is what kept the Earth in motion around the Sun.
The fable contains all the elements of a scintillating scientific discovery — an idiosyncratic genius at work, a sleight of chance and a monumental insight precipitated by witnessing the most mundane of events — a virtue of allegorical thinking. The fable, however, isn’t entirely true, but… neither is Newton’s theory.

Recommended Video for you:
Newton’s Vs Einstein’s View Of Gravity
First of all, the apple didn’t fall on Newton’s head. According to his biographer, William Stukeley, Newton witnessed the apple fall at a distance while he was in a “contemplative mood”. He pondered why the apple fell “perpendicularly” or straight towards the ground, rather than sideways or in any other unorthodox way. He later postulated that the force of gravity between two bodies pulled or attracted them towards each other with a magnitude that is directly proportional to their masses and inversely proportional to the square of the distance between them. The trajectory that the bodies undergo will be the shortest to minimize the expenditure of energy, therefore, a straight line.
Even Newton himself wasn’t particularly satisfied with his theory. He was dubious because he envisaged the force to be a push, not an inexplicable pull. This pull of gravity could either be further explained by unveiling something that Newton promptly missed or it could simply be accepted that the “magical” pull was an essential property of mass. The latter became gospel, withstanding and obscuring the truth for 400 years.
Fortunately, this dogma was rightly repudiated by Einstein, an equally formidable genius, when he made an even more preposterous claim and put forward his General Theory of Relativity. This exhibited his immense courage, for a patent clerk was challenging Newton, a veritable demigod of physics. He was challenging a view that had been worshipped for 400 years.

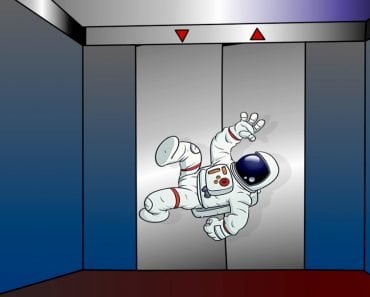
Einstein’s discovery was based on a series of thought experiments. Consider an astronaut floating in space, away from any source of gravity, and that same astronaut free falling in a planet’s gravity. The similarity of both experiences is uncanny. The astronaut must glide or sit still until affected by an external force. If an astronaut falls or floats without any knowledge of his location, say, in an enclosed lift, he cannot distinguish whether the lift is floating in deep space or through a building on Earth. In both cases, he is essentially weightless. However, if he does not experience any force, why does a free-falling astronaut accelerate? In Newtonian mechanics, this is paradoxical, as it contradicts Newton’s second law of motion – the magnitude of acceleration is proportional to the applied external force.
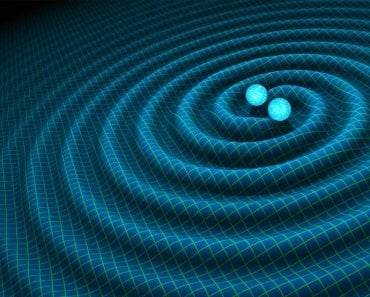
Einstein suggested that objects aren’t pulled by massive objects, but rather pushed down by the space above them. According to General Relativity, matter warps the fabric of not only space but time as well, collectively known as the continuum of space-time. The fabric is like a grid of tightly strung rubber bands; when a massive object pushes and stretches them downward, the deformed rubber bands push objects under them. The theory implied that smaller objects weren’t pulled towards massive objects but were traveling on a downward slope, as the space in the latter’s vicinity was warped by its large mass. A free-falling body, therefore, follows the straightest possible path in space-time.

Einstein developed this theory on the assumption that the laws of physics must appear the same to every observer. This is also true for planets revolving around the Sun. Orbiting planets follow the shortest path around the Sun to minimize energy. This path is an ellipse, the most efficient path in the gravity well of the Sun… but what about the astronaut’s acceleration?
Einstein’s geodesic equations signify that acceleration is a product of curved space-time. His equation explains how curvature accelerates a falling object. In the absence of curvature, the body would move in a straight line with a constant velocity, unless this motion would be disrupted by an otherwise external force. However, the most interesting aspect of the equation is the absence of mass in its expression. The magnitude of acceleration is independent of the falling body, just as the equivalence principle would demand (if you drop a hammer and a feather on the surface of the moon, they would drop at the same time).
Is Newtonian Gravity A Fallacy?
Newtonian gravity can not explain the peculiar orbit of Mercury, nor gravitational lensing, the bending of light as it passes in the proximity of a massive object, such as the Sun. Is Newton’s view entirely wrong? If yes, then why is it still ubiquitous in our textbooks?

Newton’s view is not wrong. In fact, NASA still uses his infamous laws to predict the behavior of satellites in space. His view remains extremely accurate for small bodies and low velocities. The reason why children aren’t edified on the principles of General Relativity is that the concepts are exceedingly difficult to comprehend. The geometry isn’t strictly appropriate for high school or Euclidean, and the math’s sophistication is of the highest order. The important thing to remember is that gravity is neither a push nor a pull; what we interpret as a “force” or the acceleration due to gravity is actually the curvature of space and time — the path itself stoops downward.