How Is The Mass Of A Planet Calculated?

The seemingly herculean task of measuring a planet’s mass in outer space could be done by simply applying the basic laws of physics and mathematics!

Planets are massive celestial objects, so physically weighing them is practically impossible. It’s not like we have a humongous planet-sized weighing scale just lying around! Therefore, the only way to do this is through a theoretical approach. Sounds a bit tough… how many of you, the knowledge-seekers, would volunteer to undertake such a cosmic mission?

The theoretical approach to determining the weight of the planet involves the laws of physics, and as it turns out, the approach isn’t really that complicated. The secret to the calculation, as you may expect, mostly lies in mathematics.

Recommended Video for you:

The Science Of Weighing

When you stand on a scale, the scale measures how strongly the Earth’s gravity is pulling you. Now, when it comes to measuring the weight of the planet, scale not only relies on the gravitational pull that the planet exerts, but also the mass of the planet itself. The heavier the planet, the greater its gravitational pull. So, scientists can weigh planets by measuring how hard they pull on other celestial objects. Let’s see how the planet’s weight is calculated using different approaches.

Before we begin, there needs to be one clarification. What astrophysicists often calculate is the ‘mass’ of the planet and not the ‘weight’. Yes, many of us use these terms interchangeably, but scientifically they are quite different. The mass measures how much matter is present in an object under consideration. On the other hand, weight measures how heavy the object is in a given gravitational context. To better understand this, you need to think about astronauts on a moon. Out there, he would feel much lighter, but his mass would remain the same. It’s simply that the pull of gravity on the moon is much less than what is experienced on Earth. So yes, mass is what they usually endeavor to measure.

Using Newton’s Law

To evaluate the mass of a planet, such as Earth, we can use Newton’s Law of Universal Gravitation. Using this, we know that the force of attraction between two objects is proportional to the product of their masses divided by the square of the distance between their centers of mass. In order to simplify the calculation part, we assume that their geographical centers are their centers of mass (the point where the body’s center of gravity is located).

Since we know the radius of Earth, we can use Newton’s Law of Universal Gravitation to calculate the mass of Earth in terms of the gravitational force it has on an object, i.e., its weight on the Earth’s surface, using the radius of Earth as our distance variable.

Using Kepler’s Law

In the sixteenth century, Kepler extended Newton’s work and derived an equation that we now know as Kepler’s Law. This equation finds the relation between a planet and its moon using the period of the moon’s orbit and the mass of the planet. Thus, if the distance to the moon from the planet is known, along with the time taken for that moon to orbit around the planet, then using Kepler’s third law, the mass of the planet can be calculated.

To calculate the mass of a particular planet using Kepler’s third law, we first need to know how far the planet is from Earth. This is generally done by bouncing signals off that planet and calculating the time it takes for the radar to return. Doppler radio is used for this purpose.

Thus, to calculate the mass of the planet, we need the distance of that planet from Earth, represented by R. Next, we need to know the orbital period of the moon, denoted by T. Finally, we need to know the largest angular separation of the planet and the moon, denoted by θ.

Kepler’s third law is given by the formula:

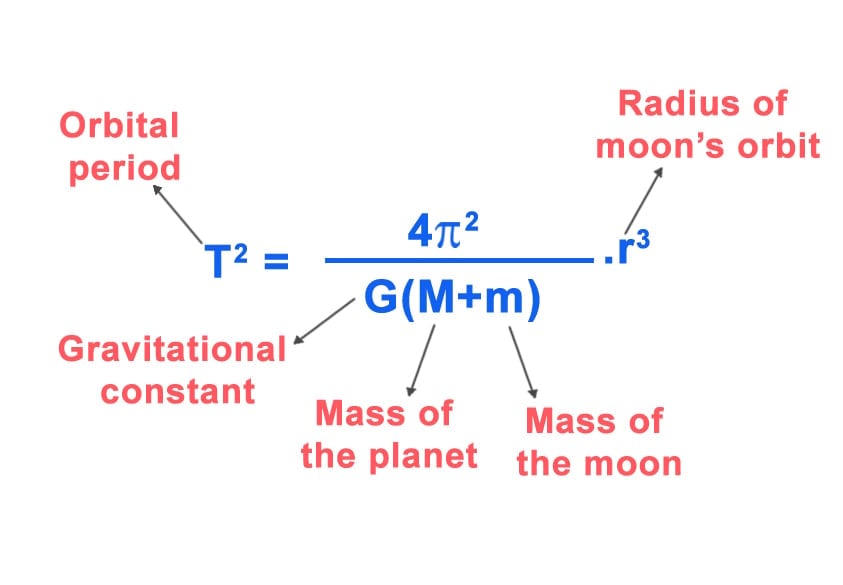
The radius of the earth, r, given in the formula above, can be calculated using the formula: r=Rθ

Rearranging the equation with Kepler’s equation:

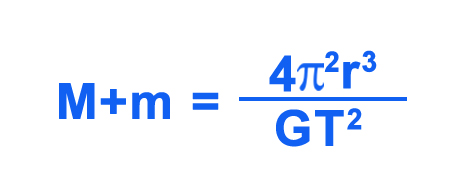
If the moon is very small compared to the planet, we assume the moon’s mass to be nil and substitute a value of m=0 and directly get the mass of the planet. This method works for most of the moons in the solar system.

However, if the moon is relatively large, such as Charon, then we need to calculate the center of mass of the planet. The distance between the center of the planet to the center of mass of the planet and moon, denoted by d, can be subsequently used to calculate the mass of the planet using the equation: Md=m(r-d)

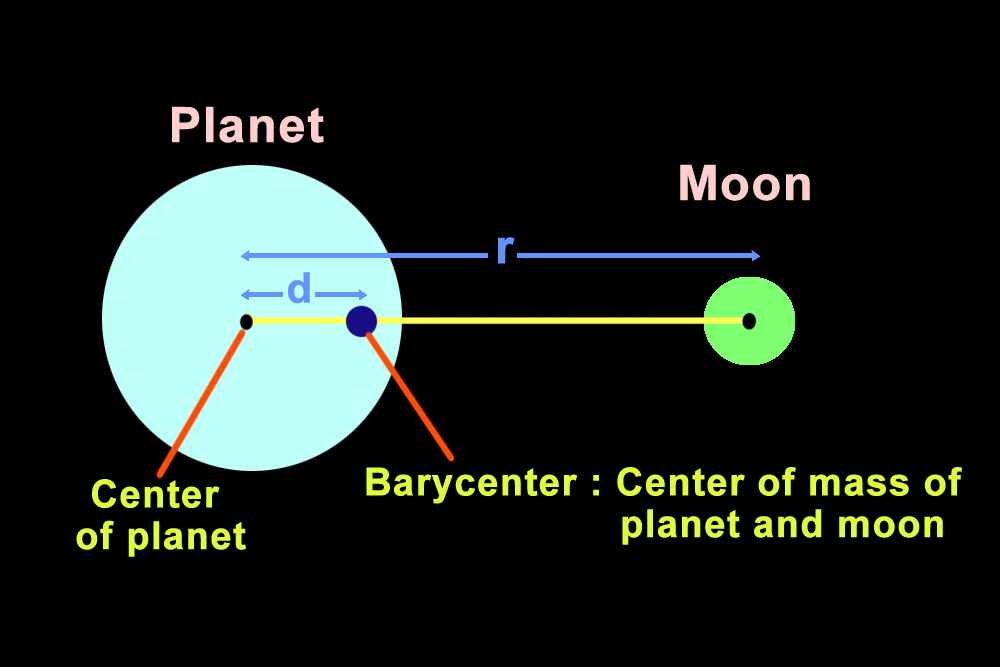
This gives the mass of the planet as:

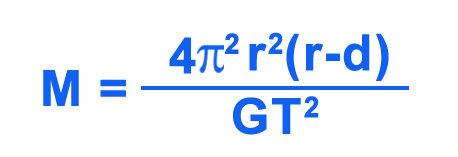
Using Geometry

Another way to guess the mass of the planet is by applying principles of geometry. However, this involves more calculative guessing than the actual measurement. If you can calculate the volume of the planet and make a rough estimate about the density of the planet based on its composition, you can get a rough value of its mass. Remember, mathematically we know that the volume of the planet (sphere) can be calculated using the formula: Volume=(4/3)*π*(radius)³

By rearranging the density formula, we can calculate the mass of the planet from this equation: mass= density*volume.

Who knew that the seemingly herculean task of measuring our planet’s weight could be done quite easily by applying the basic laws of physics and mathematics!