How Do You Measure The Distance To A Star?

The most common way to measure the distance to a star is by using the parallax method. This is where an astronomer will take note of the star’s position in the night sky and then measure it again six months later. By doing this, they can calculate the parallax angle and, using trigonometry, derive the distance to the star.

We have all heard the mind-bogglingly large numbers that are involved when talking about stellar distances. That being said, how do we even know how far away a star really is? Although there are many ways to calculate the distance between our planet and another star, three methods reign supreme. With simple mathematics and logical deductions, our astronomers have given us a much more vivid picture of the universe. Now sit down, get a cup of tea, and get your brain ready for some incredible math.

Recommended Video for you:

Parallax Method

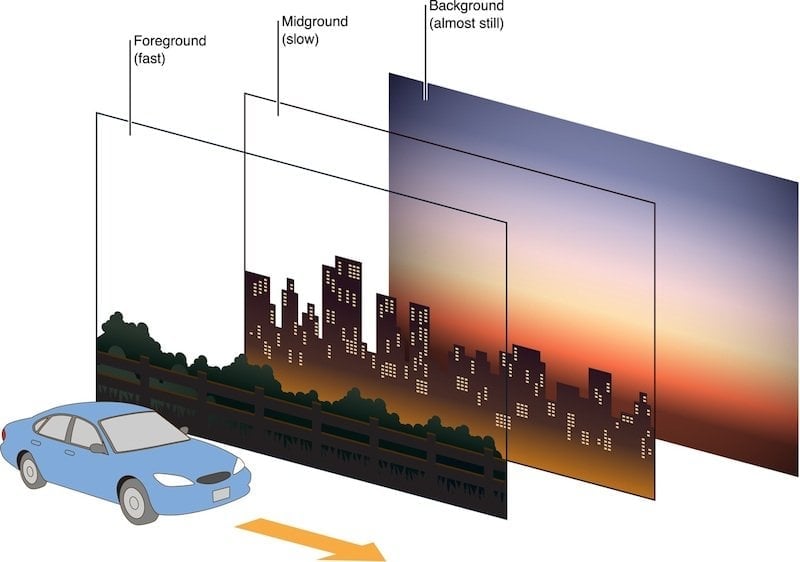
Have you noticed how whenever you look outside the window of a moving vehicle, the objects closer to you whiz by extremely quickly, but the objects farther away seem to move sluggishly in comparison? This is called the parallax effect. In the same way, when we are revolving around the Sun, the position of the stars closer to Earth move steadily from one position to another, whereas the stars farther away don’t appear to move as much. Using this principle, astronomers can calculate the distance to nearby stars quite accurately.

First, an astronomer notes the position of that star in the night sky. Then, after 6 months, the same star’s position is again measured. Remember that after 6 months, the planet is now on the other side of the Sun! Due to the parallax effect, the star’s position changes in the night sky. Then, the parallax angle is calculated after comparing the two positions.

There is a clear relationship between the parallax angle and the distance of the star. This relationship,  which can be established by simple trigonometry, is…

[The math behind this equation is fairly easy. To calculate the distance to the star, we draw a perpendicular line from the Sun’s position to the star. We know the distance from the Earth to the Sun and we know the parallax angle. Using trigonometry, we can derive tanA=opposite / adjacent, where A is the parallax angle, the opposite side is the distance from the Earth to the Sun, and the adjacent side is the distance from the Sun to the star. Thus, p=1/d. Therefore, d=1/p.]

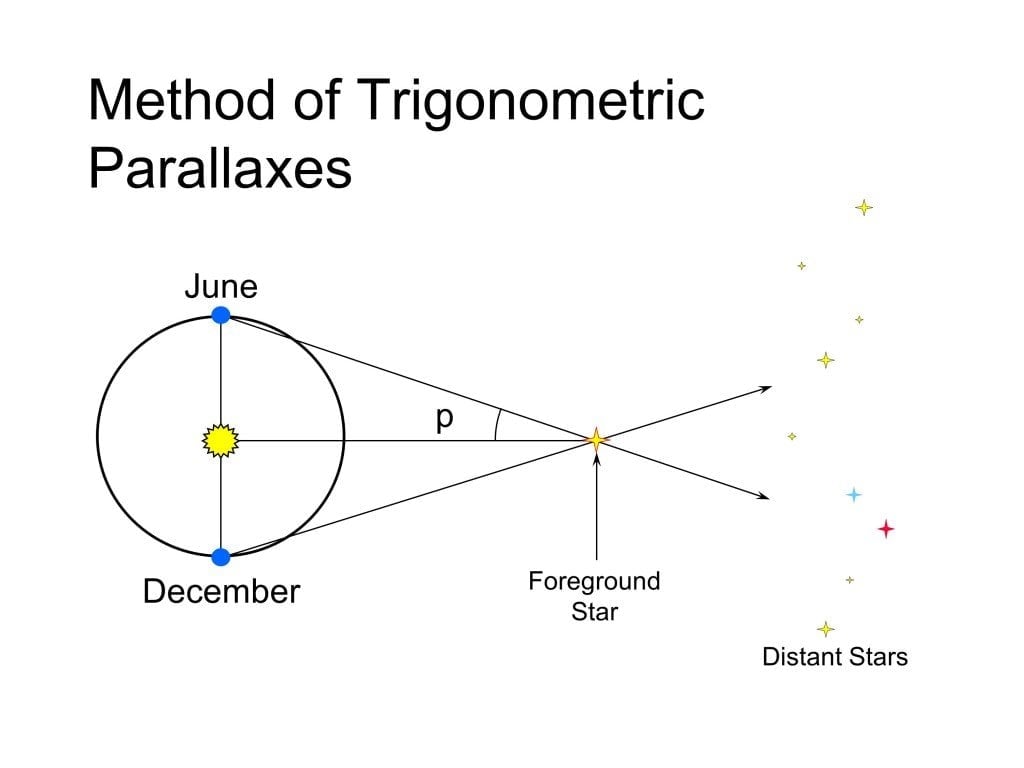
The distance between the Earth and the Sun is considered as 1 AU (Astronomical Unit). The shift in the star’s position is so small that the parallax angle is measured in a unit called arcseconds, which is a three thousand six hundredth (1/3600) of a degree. An entire arcsecond would lead to a distance measured as a single parsec (d=1 parsec=1 AU/1 arcsecond). Contrary to popular belief, light years is not frequently used as a unit of distance. Astronomers actually prefer the unit of parsecs! 1 parsec is approximately 3 light years.

The closest star to our solar system is Alpha Centauri, which is four light years away. This means that there isn’t a single star within the distance of 1 parsec except the Sun. Thus, we can conclude that if you ever feel like calculating the distance of any star, be assured that the parallax angle will definitely be less than 1 arcsecond.

If you’ve ever struggled with geometry in school, you know that trying to calculate really tiny angles can be frustratingly inaccurate. The same goes for this kind of calculation. The farther away the star is, the more difficult it becomes to measure the change in its half-yearly position.

The parallax method can therefore only be used for stars closer than 100 parsecs. However, most stars fall outside this range. Even many of the stars in our own galaxy can be more than 1000 parsecs away. So…. how do we calculate their distance?

The Color/ Magnitude Relationship

When you look up at the sky, some stars appear much brighter than others. Greek astronomer Hipparchus noticed this, and in 150 BC, sought to classify stars based on their brightness. This classification of stars on the basis of their perceived brightness is called apparent magnitude. Today, Hipparchus’ scale has been tweaked to suit the barrage of astronomical information that we have on hand by creating a more intricate scale. On this scale, the dimmer the star appears, the larger the apparent magnitude is. Some stars observed by the Hubble telescope can go up to 30 on this scale, whereas the Sun has an apparent magnitude of -26.8.

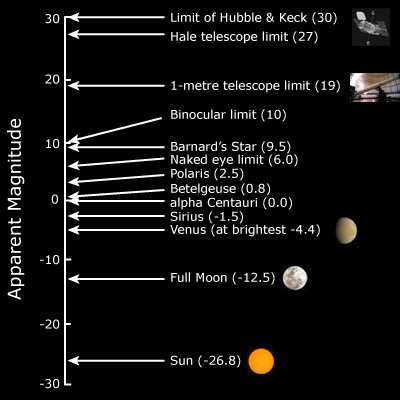
However, apparent magnitude can be very deceptive. If there is a star that’s very bright, but really far away, then it would appear dim to us. However, a dim star can be perceived as really bright if it is closer to the Earth. The actual brightness of a star is called luminosity. Luminosity is the amount of energy that a star produces every second. The different luminosities of stars are not measured in apparent magnitudes, but rather in absolute magnitudes.

But wait a minute! If we attempt to compare the two magnitudes, we can make an estimate of how far away the star could be from us. Think about it. Imagine a car heading right towards you. If you know the actual brightness of the headlight, then you can easily fathom the distance of the car from you based on how bright the light heading towards you seems.

Over the years, the relationship between the apparent magnitude and the absolute magnitude was mathematically derived to be:

 where  is the distance measured in parsecs.

Phew. So… now that we have both the magnitudes, we have a perfect way to calculate stellar distances and everyone lives happily ever after…. right?

Nope, hold up a second. We still don’t have a perfect way to establish what the absolute magnitude of a star is.

Obviously, unlike a car headlight, we can’t go right next to a star to determine its luminosity. So how do we manage it? One of the ways is by analyzing the color of the star. Stars can be white, blue, red or even yellow.

But don’t all stars look white? How do we know which ones are blue and which are red? Astronomers determine the color by looking through color filters. If a star seems brighter when looked at through a blue filter and not as bright when looked at through a red filter, then it’s a white or blue star, and vice versa.

Okay, so now we know the color of the star. White or blue stars are usually much brighter than yellow stars and yellow stars are brighter than red stars. Basically, the color of a star determines the surface temperature.

And this is how, ladies and gentleman, we determine the absolute magnitude of stars that are visible to us!

Now that we know a star’s apparent magnitude and absolute magnitude, we can finally calculate a star’s stellar distance with the equation!

Cepheid Variables

However, what about calculating distances between galaxies? Galaxies don’t have a single light wavelength, so how can we measure such vast distances?

Fortunately, the universe has gifted us with Cepheid variables. These are types of stars that are nearing their deaths. They are extremely bright – so bright, in fact, that they can be individually analyzed from a distant galaxy. They also pulsate in recurring periods. These periods are directly related to their brightness. Basically, a really bright Cepheid would take a very long time to pulse and vice versa.

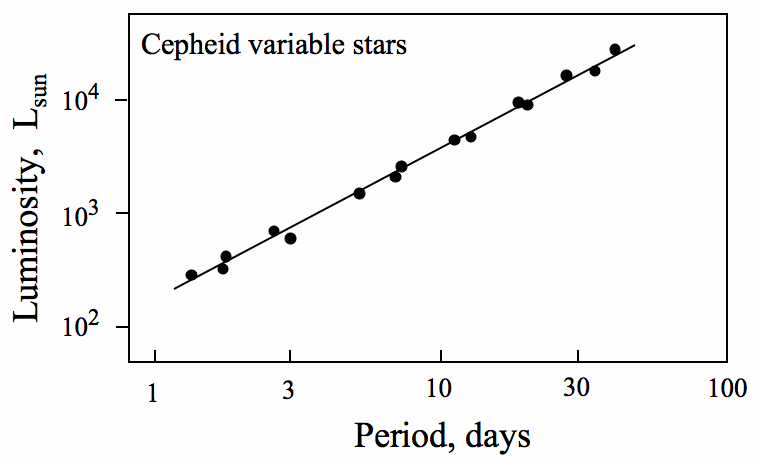
By studying the pulses, we can determine the absolute magnitude of the Cepheid. Now that we know the absolute magnitude, we can use the previous equation to discover the star’s distance, as well as the galaxy’s distance from us.

Finally! Now we can officially calculate the gigantic distances between galaxies!

Aside from all of these explained above, there are many more methods that astronomers keep coming up with to measure stellar distances. However, we’re still working with estimates and haven’t developed a perfect way to do this. Sometimes, the stars are so far away that we even have to take the expansion of the universe into account! That doesn’t matter though… it still won’t deter all of these mathematically inclined astronomers to rise to the challenge.