Table of Contents (click to expand)
There is no real escape from Earth’s field of gravity, although the reality is slightly more complicated than that, as our explanation did not account for gravity imposed by other celestial bodies, primarily the Sun. Objects hurled outside Earth are readily influenced by the Sun’s gravity because its mass amounts to 99% of the entire Solar System’ mass.
Amongst nature’s umpteen wonders, the Cosmos has monopolized the production of joy rattles that have lifted us to rare moments of ecstatic clapping. The sky was an inexhaustible source of wonderment for the ancients peering out from their caves, contemplating their place in the glinting stars. Or, for Galileo pointing his telescope towards the darkness, a raging testament of hope. Or, a teenager watching Star Trek for the very first time.
In my case, my neurons crackled with fascination when I first encountered the rings of Saturn on the cover of an old astronomy book for children (their indelible impression led me to get a tattoo on my hand). The second moment that stuck with me is the image of astronauts swimming through thin air. This was an entirely novel experience that I was missing out on, an experience somewhat reminiscent of flying.

However, like every child of that age and ken, and possibly a few adults, my conception of what made them float was based on a false assumption that Earth’s pull of gravity, at some soaring altitude in space, becomes ineffective. Thus, in a state of Zero-G, the astronauts aren’t chained down by any force and can float wherever they like.
This is far from the truth. The ISS is only 400 km above Earth’s surface, as compared to the moon, which resides some 4,00,000 km far away. If the astronauts float because they’re free from Earth’s pull, how is then the same pull driving the moon to revolve around us?
Recommended Video for you:
The Orbit
The problem of why the moon orbits us plagued Newton for years. His inquiry constituted two questions: why doesn’t the moon crash into the Earth and why, if Galileo postulated that objects travel in a direction unimpeded until acted upon by an external force, does the moon travel in a circle and not a straight line? An ingenious thought experiment led him to his answer.


Newton imagined a tall tower mounted on the surface of Earth shooting a cannonball at different velocities. When the cannonball is shot at a very low velocity, it travels along the straight surface of Earth and falls not far from the tower, tracing the trajectory of a parabola. However, when the cannonball is shot at a higher velocity, it travels straight along Earth’s horizontal surface, as well as slightly above the curved surface.
As the velocity progressively increases, the cannonball travels greater horizontal and vertical distances. Newton realized that there must be a magic velocity at which the cannonball falls at the same rate as the Earth curves! Its inertia would perfectly cancel the pull of gravity, such that the resultant force transmutes into a centripetal force. The force of gravity then emulates the tension in a string attached to a stone swinging in circles around you.
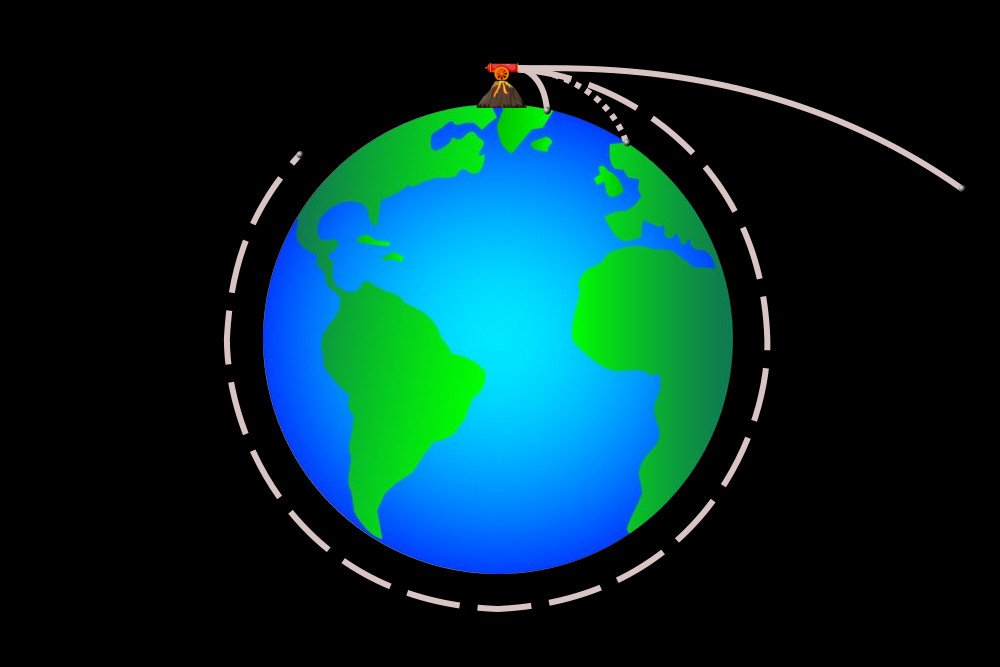
At a certain speed, the projectile falls completely around the Earth, meaning that it is in perpetual fall. Similarly, the astronauts, the ISS, and the moon are perpetually falling towards the Earth. However, the ISS and astronauts fall at the same rate, which is why they feel weightless, like falling in a lift through a 20-story building or floating at the crest of a roller coaster. So, the ISS hasn’t escaped Earth’s pull at all. In fact, it is subject to about 90% of the gravity that we are subject to on the surface.
Infinity And Beyond
While the moon takes a month to saunter around us, the ISS only takes 90 minutes. Between these two lie orbits where, at a certain velocity, satellites achieve a lap time of 24 hours, such that they can dedicatedly surveil a single area beneath them. The point is, between the moon and the Earth, there is no point where Earth’s gravity is ineffective, but what about any point beyond the moon?

Well, still no. Gravity can grow tragically weak, but not truly ineffective. It follows an inverse square law, according to which its strength diminishes with the square of the source’s distance. Even though larger distances might render the force puny, its effects are still measurable. Consider LIGO’s achievement of recording the aftermath of a catastrophic collision of black holes that sent extremely tiny gravitational waves blistering at the speed of light towards us.
The pull has a domino effect. For example, let’s say that the pull on an object relaxing at some remote point in space is 0.001% of what it is at Earth’s surface. This pull will lure the object, albeit very gradually, towards Earth, such that a slight acceleration will bring the object closer towards it. Now that the distance is decreased, the pull gradually strengthens. It pulls the object more starkly until it progressively heads towards Earth, and finally, crashes into it.
So, even though a tennis ball hurled at escape velocity allows it to dart straight upwards and never come back, there isn’t any real escape from Earth’s field of gravity. The reality is slightly more complicated than that, as our explanation did not account for gravity imposed by other celestial bodies, primarily the Sun.

Objects hurled outside Earth are readily influenced by the Sun’s gravity because its mass amounts to 99% of the entire Solar System’ mass. This is true for distances even less than 250,000 km, which is why the moon (4,000,000 km away), along with us, revolves around it.
However, if one assumes that the Sun and every other celestial body has no say whatsoever, then the reach of Earth’s gravity is practically infinite, pulling on each and every atom that is quivering in even the most remote corners of the Universe.
References (click to expand)
- Are astronauts really weightless? - Phys.org. Phys.org
- Newton's Cannonball and the Speed of Orbiting Objects. Bucknell University
- Is There Gravity in Space?. Space.com
- How close do you have to come to the Earth to be influenced by its gravity? (Advanced) - Curious About Astronomy? Ask an Astronomer - curious.astro.cornell.edu