Table of Contents (click to expand)
Matrixes come in various form and shapes. But there is one matrix whose usefulness extends to a wide array of fields from physic to engineering.
Matrixes, just like people, come in all shapes, sizes and forms. There are many different kinds of matrices, depending on the rank, order and even what the matrix contains within it. If you’ve taken high school linear algebra, then you have a decent idea of what the different types of matrixes are, based on various parameters.
Now, the primary function of a matrix is to help us simplify calculations; ironically, most complex calculations performed by computers are also broken into matrices. Now to understand the nuances of a Jacobian Matrix, we first need to understand Vector Calculus and some basic Matrix properties.
Recommended Video for you:
What Is Vector Calculus?
Vector calculus can be defined as the branch of mathematics that deals with the differentiation and integration of vector fields. A vector field can be thought of as a set of vectors that all align in a particular direction in space (or more precisely, Euclidean space).
Vector calculus plays a vital role in differential geometry and differential equations. Differential geometry is a mathematical discipline that uses the techniques of differential calculus, integral calculus, linear algebra and multilinear algebra to study problems in geometry. Differential equations, on the other hand, are equations that consist of multivariables, which signify a certain rate of change.
The primary application of vector calculus is in the field of physics. To make a generalized statement, vector calculus is used in all strata of physics. It is employed in classical mechanics, especially fluid mechanics, and is also the foundation for electrodynamics.
More high-end topics such as General Relativity and Quantum Mechanics also use aspects related to simple vector calculus, primarily tensor calculus and vector spaces. Another subject that comes as a surprising related genre is computer programming and graphics.
Also Read: What Exactly Is Calculus And How Do We Use It In Everyday Life?
What Is A Matrix?
A matrix can be defined as a rectangular array of numbers or other mathematical objects in which operations such as addition and multiplication are defined. Matrices primarily come in two forms: real and complex matrixes. The difference in these matrices lies in the fact that the elements present within the matrix are either real numbers or complex numbers. However, the kinds of matrices we’ll be dealing with are a bit unique and a something of an anomaly to the family of matrices.
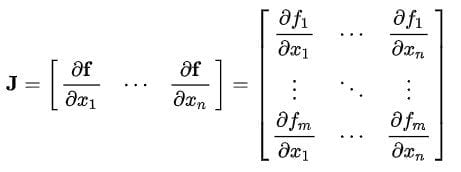Matrices are used much more in daily life than people may realize. They are in front of us every day when going to work, at school and even at home! A square matrix can represent the linear transformation of a geometric object. In physics-related applications, matrices are used in the study of electrical circuits, quantum mechanics and optics.
Engineers use matrices to model physical systems and perform accurate calculations that are needed for complex mechanics to work. In robotics and automation, matrices are the basic directional components for the robot’s movements. The inputs for controlling robots are obtained based on the calculations from matrices, which result in very accurate movements.
Also Read: Is There Anything More Complex Than Complex Numbers?
Characteristics Of A Jacobian Matrix
Now that we have a basic understanding of vector calculus and matrices, we will be able to more accurately define and explain a Jacobian Matrix. A Jacobian Matrix can be defined as a matrix that contains a first-order partial derivative for a vector function.
The Jacobian Matrix can be of any form. It can be a rectangular matrix, where the number of rows and columns are not the same, or it can be a square matrix, where the number of rows and columns are equal. Let’s try to represent a Jacobian Matrix in a more rigorous mathematical sense.
The f: ℝn → ℝm is a function that takes as input the vector x ∈ ℝn and produces as output the vector f(x) ∈ ℝm. Then, the Jacobian matrix J of f is an m×n matrix, usually defined and arranged as follows:
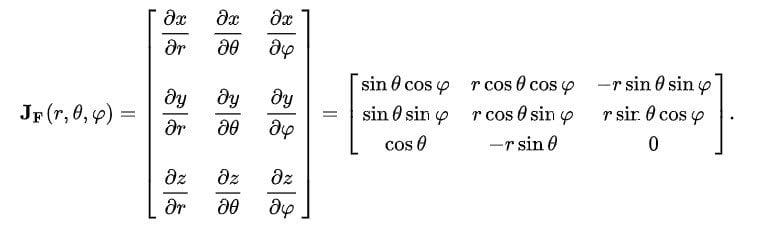
The entry for this matrix is usually a variable like x. Knowing this is highly imperative, as this indicates that the function is differentiable at the point x. Being differentiable at a point indicates that the matrix can be mapped and given a geometric and visual approach to understanding the equations at hand.
The most important kinds of Jacobian Matrix are the Polar-Cartesian and Spherical-Cartesian. These matrices are extremely important, as they help in the conversion of one coordinate system into another, which proves to be useful in many mathematical and scientific endeavors.
The importance of the Jacobian Matrix is critical in all fields of mathematics, science and engineering. One prime example is in the field of control engineering, where the use of Jacobian matrices allows the local (approximate) linearization of non-linear systems around a given equilibrium point, thus allowing the use of linear systems techniques, such as the calculation of eigenvalues (and thus allowing an indication of the type of the equilibrium point).
Jacobian matrices are also used in the estimation of the internal states of non-linear systems in the construction of an extended Kalman filter. Basically, we can conclude by saying that Jacobian matrices maintain a truly unique and important place in the world of matrices!
