Hilbert Space is a mathematical space proposed by David Hilbert, a German mathematician. It is an extension of Euclidean space for infinite dimensions.
Have you ever wondered how physicists are able to understand particles and waves? Also, how do they study them?
Let’s try to understand their process with an analogy!
Recommended Video for you:
The Need for Mathematical Space
To understand how a ball behaves when it is thrown vertically upwards, it’s important to study the surroundings of the ball. This includes factors like acceleration due to gravity, air friction, wind velocity and other variables. The surroundings or the space where the ball is thrown also impacts the behavior of the ball.
For example, if the ball is thrown on Earth, we know that the ball will experience an acceleration due to gravity, a rate of 
towards the earth. Now, if the same ball were thrown on the surface of the moon, where the force/acceleration due to gravity is reduced, owing to the mass of the moon, we know that the ball would behave differently. Hence, it’s very important in physics to understand the nature of the space where a given object is being studied. This helps us compute the behavior of that object mathematically in a convenient manner.
Thus, choosing or defining a particular space makes it easy for a physicist to understand a particle/wave and study its behavior conveniently.
Another analogy similar to the one mentioned above would be measuring the weight of an object in the earthly environment, versus the extraterrestrial environment. So, while studying both these cases, it’s very important to note the change in the value of acceleration due to gravity; as a result, it is observed that the value of weight measured changes drastically, despite the fact that the mass remains unchanged. Thus, it is important that when we choose a mathematical space to study an object, we must define the space in such a way that the changing parameters are taken into account.
How does a mathematical space work?
Let’s assume that there is a mathematical space called Addition Space. Whatever entities I drop into this space, it will add together and give the sum of them all. For example, if we have two waves in that space, then the resultant wave would be a simple addition of them.
Two waves being added
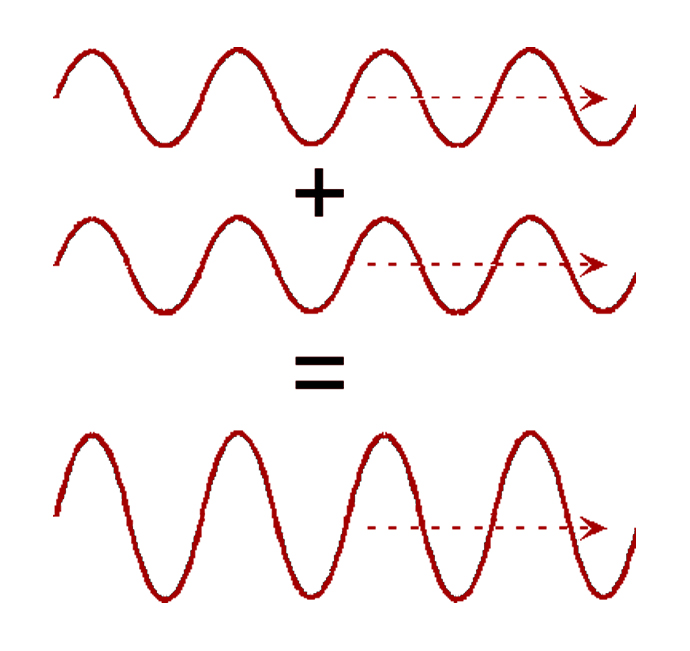
In a similar manner, different spaces are defined to study various particles, objects or waves. Hilbert space is one such mathematical space that makes it convenient for physicists to study quantum particles. Quantum particles demonstrate behavior that cannot be studied under classical laws.
Thus, we can say that particular mathematical spaces allow numerous operations based on their nature and dimensions. The universe we live in has curvature and more than one dimension.
Mathematical Spaces and their Functionalities
In general, space is a set of points with some relational properties. Space is referred to as a mathematical space, since different mathematical operations are performed within it. Some properties of the space are:
- We perform various operations in them, like, adding vectors, intersections, unions, cutting and pasting and measuring different sizes.
- Various relational operations, like convergence and proximity relations, are performed.
- Transformations are performed in the spaces, along with many varied mathematical operations.
History
It all goes back to the study of real numbers, most popularly referred to as Euclidean Space. Initially, during the times of the Greeks, real numbers were considered to be just integers and rational numbers, until the discovery of 
. The discovery of irrational numbers led to the discovery of transcendental numbers (for example pi and e). This discovery increased the complexity of real numbers, and we now know that it consists primarily of transcendental numbers.
The pun is much simpler than understanding all the purposes of pi.
We also know how significant these real numbers are in science today.
Different Types of Spaces
In Euclidean space, all geometrical operations could be performed, like measuring the distance between two points, studying geometrical shapes and other common calculations. However, our universe is known to be a non-Euclidean space.
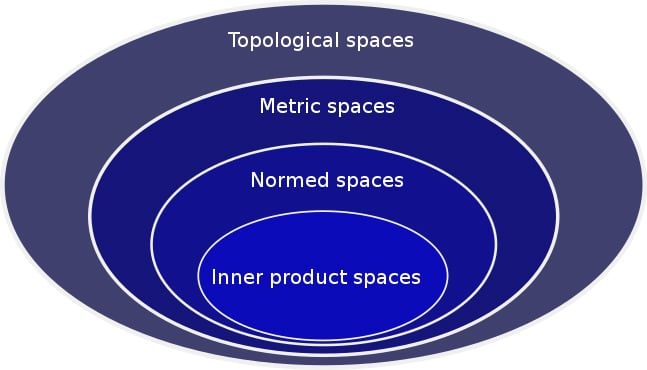
With further discoveries in algebra, geometry, calculus and set theory, a new perception of space for performing operations began to take shape. Generally, these mathematical spaces were broadly studied under four major categories (there are many other mathematical spaces, based on the object/topic of our study).
- Linear Spaces
- Topological Spaces
- Metric Spaces
- Normed and Banach Spaces
Linear Space
Linear spaces are vector spaces that are spread uniformly in all directions and do not have any curvature. The derivative of functions at a given point is linear in operation, since a derivative at a particular point in a function is nothing but a tangent.
Visualization of Linear Space (Photo Credit : Quartl/Wikimedia Commons)
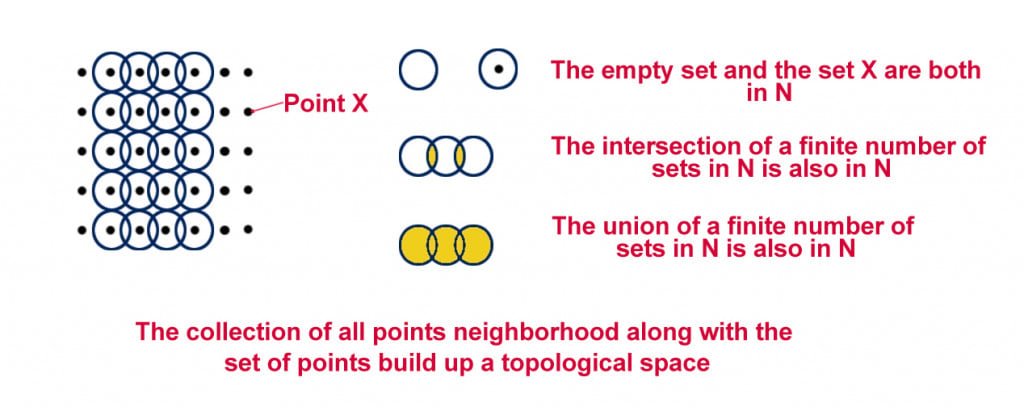
Topological Space
Topological spaces gained momentum in the early 20th century. They provide a general framework for continuity, convergence and compactness of functions. Basically, they are used to study small aspects of a larger structure in detail with more clarity. It is famously described as rubber sheet geometry, i.e. the study of geometric properties that are insensitive to stretching and shrinking and shrinking without tearing or glueing.
Topological Space
Metric Space
Metric space is used to measure the distance between two points and general geometric operations. Metric space is a topological space, but not all topological spaces are metric spaces.
Banach and Normed Space
Banach and Normed spaces are spaces that incorporate the interaction of both algebra and geometry. Norm generally means the length, thus these spaces provide for more powerful results.
The different mathematical spaces and their mutual association. The smaller circles are part of larger ones, but not vice versa! (Photo Credit : Åshild Telle/Wikimedia Commons)
With this basic understanding of mathematical spaces, we can now try to understand what Hilbert space is!
Hilbert Space
In physics, we study objects traveling at speeds comparable to that of light under Relativistic mechanics, and other lower and real-world speeds under non-relativistic mechanics. Thus, Hilbert space is useful to understand and study non-relativistic Quantum Mechanics. Hilbert space is a linear space with an operation of the inner product, i.e. scalar product, and is similar to the metric space in totality. The various wave functions in quantum mechanics that describe the states of quantum particles live in Hilbert space. It is a fusion of algebra, topology and geometry.
In quantum physics, a particle is considered to be an object that is localized in a physical space, i.e., 3-Dimensional Euclidean Space. The particle is described in terms of states, observables or expectation values these are given by vectors in Hilbert Space. Thus, this space aids in finding the probability density of a quantum particle in the space.
Euclidean space could accommodate almost all functions, but was limited in terms of dimensions, i.e.. Euclidean space is considered to be a finite-dimensioned space, while Hilbert space is an extension of Euclidean space and is an infinite-dimensioned space.
Hilbert space is both a vector space and Normed Space (Photo Credit : Åshild Telle/Wikimedia Commons)
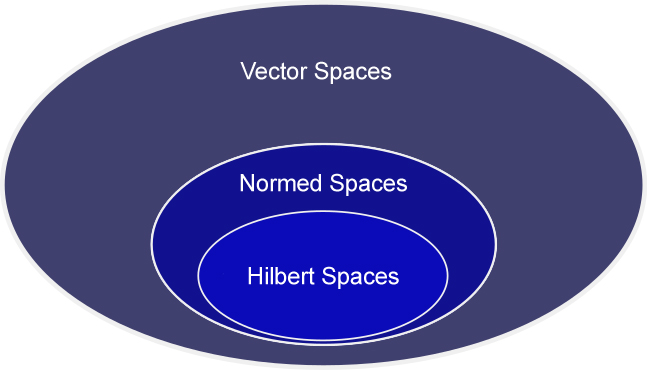
Thus, Hilbert space is a mathematical space with infinite dimension. Almost all operations, from simple arithmetic to complex mathematical problems, can be solved in Hilbert space. The most popular application of Hilbert spaces is in Quantum Mechanics. With the help of vectors, which are commonly referred to as Eigen Vectors, Hilbert spaces help in solving the mysterious behavior of quantum particles. They allow the quantum particles to undergo transformations by values called Eigenvalues and establishes a relation between these vectors and values to solve particular quantum problems.
