How Is Crystal Structure Determined?

Crystal structure is determined by X-ray diffraction. A beam of X-rays strikes the crystal and the diffraction pattern is then used to study the structure,

Matter can broadly be classified into two categories based on its internal structure—amorphous and crystalline. Amorphous materials are those that lack long-range order and structural symmetry, while crystalline structures are those that have a repeating molecular structure over long distances and symmetry. Both solids and liquids exhibit crystalline and amorphous structures.

Many substances of functional, economic, and aesthetic value, such as table salt, diamond, snowflakes, quartz, silicon-germanium semiconductors, proteins, and more, are crystalline in their structure. Determining their structure and classifying them explains many of their physical and chemical properties.

For example, LCD technology uses liquid crystals whose structure is modified by varying an electric field that modulates light (changes polarization, amplitude, or phase) by passing through it. Workout supplements that contain a mixture of various proteins can be verified to be genuine, rather than counterfeit.

The development of such devices requires an understanding of crystal structure and its effect on the physical and chemical properties of a given substance.

Recommended Video for you:

Crystal Structure Basics

Imagine a Rubik’s cube. It is made up of smaller, indivisible, and identical cubes. Those small cubes are called unit cells. Similarly, all crystals have unit cells that make up the bulk of the crystal when they are allowed to accumulate. To understand the geometry of a unit cell, it’s important to introduce the concept of a lattice.

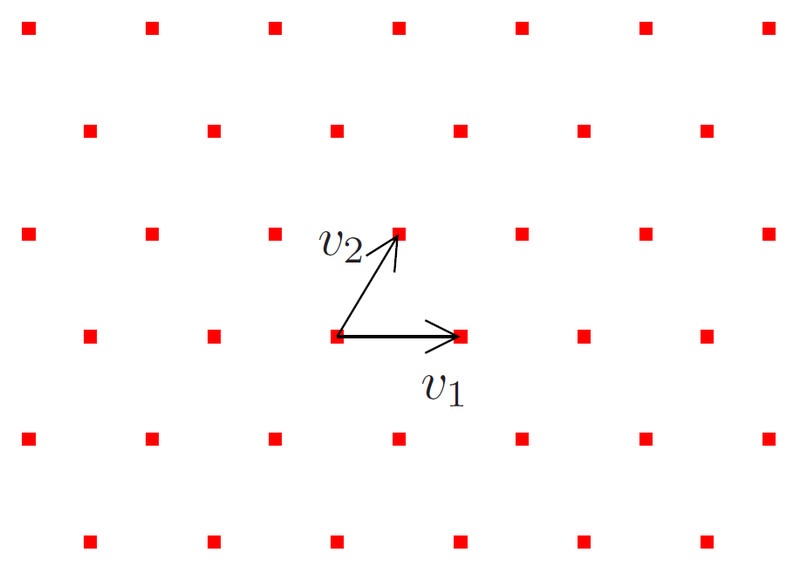
A lattice is a regular arrangement of points/dots extending infinitely in all directions. Any arbitrary point in this lattice is surrounded by other points from all directions (diagonal and sideways). These points serve as an abstract realization of real 3-D space. These points can be joined together to form different shapes, like cubes, hexagonal prisms, cuboids, rhomboids, tetrahedrons, and so on.

The many different 3-D structures act as unit cells for different crystals. They have different sets of parallel planes inclined at various angles to each other, which gives them different optical properties. The distance between crystal planes is about ~10^-10m (picometers).

Thus, if light of a similar wavelength could be employed, the crystal planes would cause the diffraction of light and result in a diffraction pattern. This diffraction pattern is different for different types of unit cells. X-rays have wavelengths ranging from 10^-10 m to 10^-9 m, which makes them undergo diffraction when interacting with crystals.

The usage of X-rays to study crystalline structure is called X-ray crystallography.

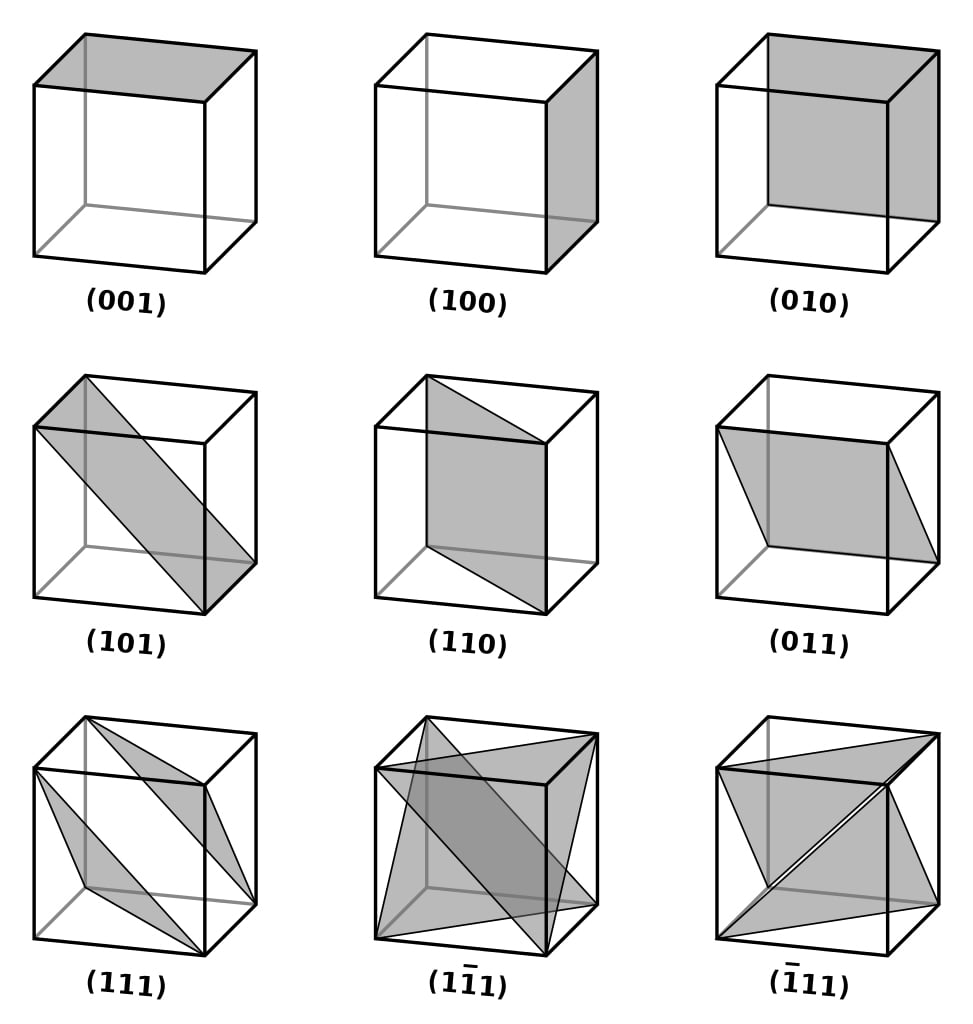
Miller Indices

Imagine a unit cell placed on a 3-D coordinate axis. The unit cell has a set of parallel planes extending in all directions. The planes may or may not be parallel to the coordinate axes. If the planes and axes are parallel, then there would be no intersection of the two and the intercept (the point at which the plane intersects the axis) would be infinite. However, if they are not parallel, then the planes would eventually intersect the coordinate axes, and the intercept would be finite.

Since there are three coordinate axes, three intercepts are required to measure the planar orientation of the crystal. Let the intercepts of the crystal planes with the (x, y, z) axes be (p, q, r), respectively. Miller Indices–

give the orientation of a crystal plane. Since 1/p, 1/q, and 1/r is decimal, LCM of p, q, and r is multiplied to make (h, k, l) integers.

For a cubic unit cell with lattice parameter a (edge length), the distance between two parallel planes (interplanar distance) is-

.

X-Ray Crystallography

There are two widely used methods of X-ray crystallography, namely the rotating crystal method and the powder method. In both, the principle is broadly the same, i.e., illuminating a crystal sample with X-rays and then studying the diffraction pattern of the resultant beam to infer structural information.

Rotating Crystal Diffraction Method

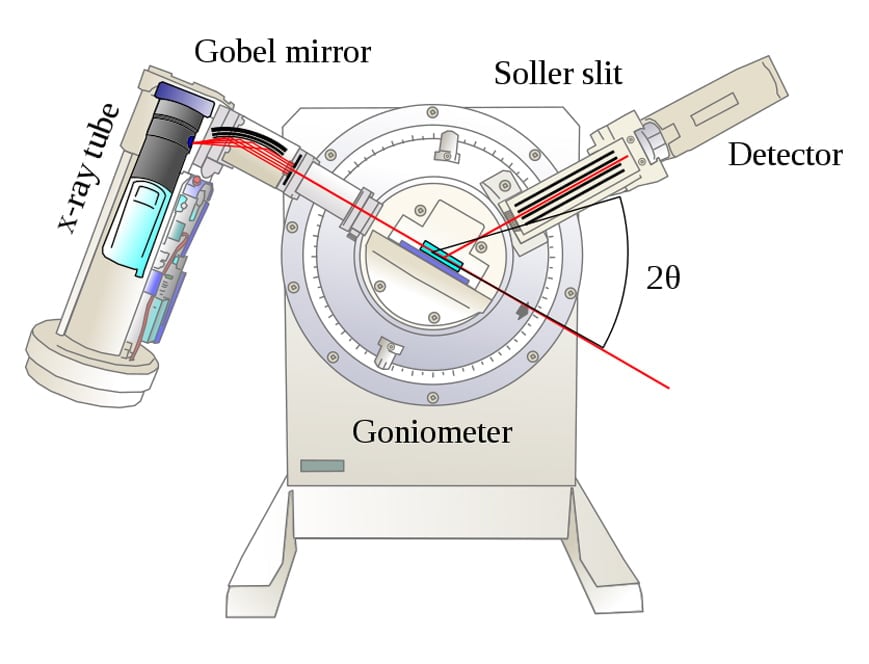
A pure crystal sample, whose planar orientation is unknown, is placed on a holder. An X-ray beam (collection of parallel rays) from a tube strikes the powdered crystal. The crystal can be rotated about multiple axes, which allows for different crystal orientations with respect to the incoming X-ray beam.

Imagine a ray of light striking a plane mirror. If the ray is parallel to the mirror, there would be no reflection, but if the ray is inclined at an angle with respect to the mirror, it will be reflected. Similarly, if the X-ray beam is parallel to the crystal planes, it would pass through without any interaction with the crystal and no diffraction would occur. However, if the planes and the beam are inclined, a strong diffraction pattern would be observed.

Imagine two parallel planes separated by a distance d. As the X-ray beam reaches the crystal, the set of parallel planes acts as a set of separate, parallel mirrors. The interplanar distance is d. When the beam reaches the crystal, its constituent rays have to travel different lengths to reach the two planes (since the planes are separated by d). This introduces a path difference (difference in the distance travelled) between the two rays.

A change in path difference translates to a change in the phase difference of the X-rays. Thus, the two rays, having some phase difference, traveling the same direction, and having the same frequency, superpose with each other, causing interference. This interference pattern (a series of intensity peaks and lows) is recorded on a photographic plate. The series of intensity peaks and lows are distributed evenly about a central point.

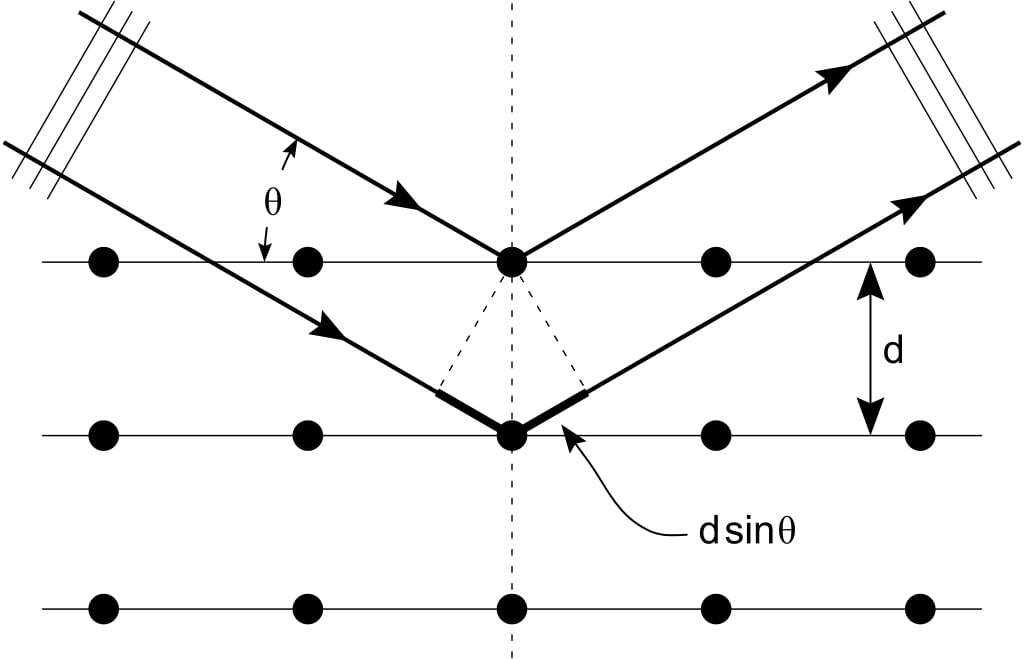
Let the angle of incidence of X-rays be . The condition for constructive interference (bright spot), given by Bragg’s Law is,

  where,

= wavelength of X-rays,

= n^th intensity peak about the central point,

d = interplanar spacing.

Here, the angle is measured using scales on the instrument, and the wavelength, , is already known. Thus, d can be calculated.

Using Bragg’s equation, d_hkl can be calculated. When the crystal is rotated, a different set of parallel planes starts reflecting. The interplanar distance for these planes is calculated and then a new set of planes is brought into focus. In this manner, all the possible d_hkl values (i.e. interplanar distances of all the planes) of the crystal are calculated.

Now,

For the first bright spot, n=1,

Since the quantity on RHS is constant (lattice parameter and wavelength), using simple trial and error, the (h, k, l) values can be calculated for an unknown crystal (i.e., the precise value of a is unknown). Since many crystals have already been measured, (h, k, l) can be found from lookup tables.

The Verdict

X-ray diffraction is an important tool in solid-state physics. From the determination of crystal structure to verifying crystal constituents of items we use every day. In fact, the Nobel Prize for Physiology in 1962 was awarded for the discovery of the molecular structure of nucleic acids!