Table of Contents (click to expand)
A Matrioshka brain is a proposed megastructure that can extract immense computational capacity from our proximate star. Robert Bradbury, who proposed this concept, derived the name from the nesting Russian Matryoshka dolls. This model is heavily inspired by the theoretical Dyson sphere, which comprises layers upon layers of Dyson spheres around the sun.
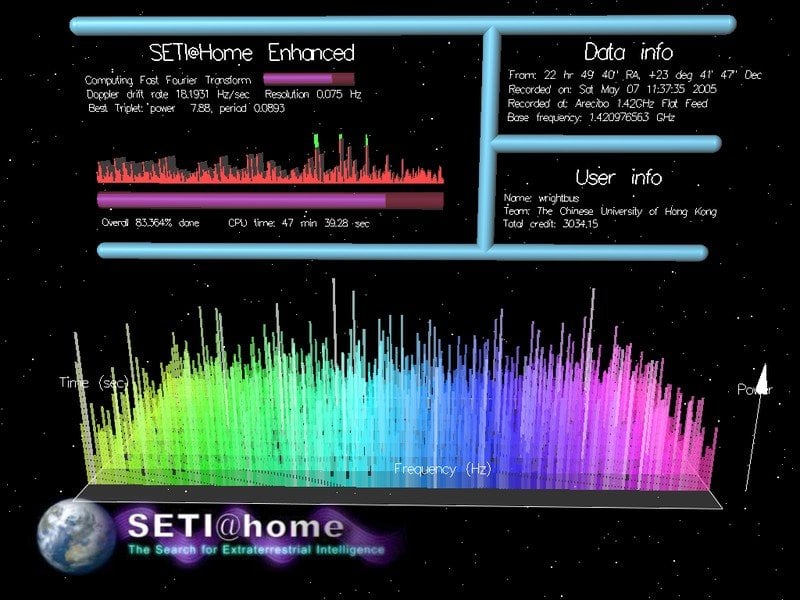
Do you know that your computer can help in finding aliens? It may sound strange, but it’s true. The SETI (search for extraterrestrial intelligence) organization has an application called SETI at home for doing just that! Now, that doesn’t actually mean that you can just download the application and discover little green men right at home, but what this application does is allow the SETI researchers to use your computer (when it’s not in use) to crunch data in an effort to find extraterrestrial intelligence.
Recommended Video for you:
Matrioshka Brain
The idea behind this technique is pretty brilliant. Instead of burning hundreds of thousands of dollars to buy supercomputers for processing vast amount of cosmological data, they simply distribute processing power throughout computers all around the globe. You can go to their site, download this application and let SETI researchers use your computer for processing whenever it’s idle. Basically, it turns the entire Internet into a giant supercomputer!
What if we need processing prowess that won’t be satisfied by the arrays of all the computers on Earth used in conjunction? In that scenario, we would need to think beyond our planetary resources to derive the power needed for such computations. For example, what if we could encapsulate the entire sun to build a supercomputer? Well, that’s the main idea behind the Matrioshka brain!
A Matrioshka brain is a proposed megastructure that can extract immense computational capacity from our proximate star. The Matrioshka brain model is heavily inspired by the theoretical Dyson sphere. Robert Bradbury, who proposed this concept, derived the name from the nesting Russian Matryoshka dolls.

The Need For Matrioshka Brain
With our steady progress in scientific thinking, we have discovered a number of apparently dependable methods for inspecting the world around us. We have learned what the Earth is made of and how to tinker with it to fulfill our needs. For instance, we extract fossil fuels from the earth to power our industries.
However, what we have learned and developed technologically thus far is likely to become insufficient if our needs continue to grow rapidly, while our earthly resources fall short. At this point, we could be left with no choice but to expand and explore beyond our planet. One hypothesis is that the needs of advanced civilizations of the future will require them to gulp much more energy than their predecessors, which will lead to the creation of megastructures like a Dyson sphere, which wold encompass a star (the Sun, in our case) to harness the enormous amounts of energy contained there.

Freeman Dyson, who originally conceptualized Dyson spheres, saw this sphere as a potential place to live. What Robert Bradbury came up with was an extension to this idea—what if a Dyson sphere was transformed into a supercomputer—the most powerful computing machine in the universe?
Bradbury’s Matrioshka Brain
In his anthology “Year Million: Science at the Far Edge of Knowledge“, Robert Bradbury envisioned that in the future we might develop the technology to build a set of nested star shells orbiting the Sun—similar to a Dyson swarm. Like Russian Matryoshka dolls, wherein the dolls are nested inside other dolls, i.e. smaller dolls fitted inside larger dolls, he saw this megastructure formed from layers upon layers of Dyson spheres encompassing the sun to harness its energy and power the giant supercomputer. This design is why he called it “Matrioshka Brain”.
To work as a super-giant computer, a Matrioshka brain would take power from the star and spread it through the network of encompassing shells. One shell would acquire as much energy as it could from the star and would then transfer the unused energy to another larger processing shell surrounding it. This would repeat until all the energy was consumed. The inner shells would work at a temperature tantamount to the star, while the outermost shell would be near the temperature of interstellar space.
In Pursuit Of Matrioshka Brain
It goes without saying that the scale of engineering and the quantity of resources required for such an ambitious project is beyond what humans can currently muster. One of the methods of implementing Matrioshka brain would be through ‘self-replicating’ machines, as proposed by George Dvorsky.
Interestingly, efforts have begun in this exciting direction. Billionaire entrepreneur Peter Diamandis recently created a company called Planetary Resources with the goal of mining asteroids to make the infrastructure for building a Dyson sphere. Another company with the name Made in Space is researching and working on designing 3D printing technology that would work in space with the ultimate motive of setting up factories that could replicate themselves in outer space.
However, assessing the current pace of progress, Bradbury opined that humans would be able to build a megastructure roughly by 2250. He feared that in the process of building it, we may exhaust all the silicon from Venus, assuming that silicon would be one of the important raw materials. That being said, if we are successful, the first Matrioshka brain would have a processing capacity in excess of one million times the capacity of the billions of computers we currently have on Earth—combined!