What Is Molar Heat Capacity And How Do You Calculate It?

Molar heat capacity is the amount of heat required to raise the temperature of 1 mole of a substance by 1 unit & is calculated by dividing heat capacity by the total number of moles.

Have you ever wondered why we don’t burn ourselves while using a pan?

Of course, it is the handle that protects us, but why doesn’t it get as hot as the pan itself? After all, it is exposed to the same amount of heat.

For starters, a panhandle is typically plastic, which means that it is a poor conductor of heat. Also, given the same amount of heat exposure, the rise in the temperature of the plastic handle is much less than that of the metal portion. This is attributed to the handle’s high heat capacity compared to the metal the pan is made from.

Heat capacity is defined as the amount of heat energy required to raise the temperature of a given mass of a substance by one unit. Specific heat capacity and molar heat capacity are properties derived from the heat capacity of a material.

Recommended Video for you:

Specific Heat & Molar Specific Heat

Heat capacity is an extensive property, i.e., it depends on the amount and size of the substance. A modified form of heat capacity (called specific heat capacity or simply specific heat) is commonly used in physics. Specific heat doesn’t vary with the amount of the substance and is, therefore, a more useful property.

Specific heat is defined as the amount of heat required to raise one unit of mass of the substance by 1 unit of temperature. Mathematically, it is the heat capacity of a substance divided by its mass. The formula for specific heat is:

Here, c is specific heat and has units J/kg.K, C is the heat capacity of a substance in J/K, and m is the mass of the substance in kilograms. Another very important formula used to express specific heat is:

Here, too, c stands for specific heat, ΔQ is the difference in heat energy in joules, m is the mass of the substance, and ΔT is the difference in temperature in Kelvin.

In chemistry—where the amount of a substance is usually measured in moles, not grams—further modifying the definition and formula of heat capacity to include moles makes things a lot easier.

Molar heat capacity is defined as the amount of heat required to raise 1 mole of a substance by 1 Kelvin. Like specific heat, molar heat capacity is an intensive property, i.e., it doesn’t vary with the amount of substance.

Mathematically, it is the heat capacity of a substance divided by the number of moles and is expressed as:

Here, c_m is molar heat capacity (J/K.mol), C is heat capacity (J/K), and n is the number of moles (mol).

Specific heat and molar heat capacity may not vary with the amount or size of the substance, but their values fluctuate based on the method of determination.

When heat energy is supplied to a substance, particularly gases, the temperature rise is accompanied by an increase in either volume or pressure, and sometimes both. These phenomena are explained by Charles’ law and Gay-Lussac’s law.

C_P,m & C_V,m are often used to represent molar heat capacities measured at constant pressure (isobaric) and constant volume (isochoric).

The value of molar specific heat at constant pressure is always greater than that measured at constant volume. This is because heat supplied at constant pressure is used to produce work and also expand in volume. In contrast, heat supplied at constant volume is entirely utilized to increase the temperature of the substance.

The ratio of C_P and C_V is called the heat capacity ratio or adiabatic index (γ = C_P/C_V), and is an important term when working with reversible processes in thermodynamics. On the other hand, the difference between C_P,m & C_{V, m} is equal to the universal gas constant R. The expression C_P,m – C_{V, m} = R is called Mayer’s relation.

How To Calculate The Molar Heat Capacity Of A Substance?

Determining a substance’s heat capacity and subsequently its specific heat and molar heat capacity is not exactly rocket science. The values can be calculated by simply breaking down their definitions, finding individual quantities (amount of heat supplied or removed, initial temperature, final temperature, the mass, and the number of moles of the substance), and substituting them in their respective places in the formulas.

Step 1: Finding Heat Capacity

As already defined, heat capacity is the amount of heat required to raise the temperature of a known quantity of the substance by one unit. The definition is expressed as:

Here, C is heat capacity, Q represents heat energy, and ΔT is the temperature difference. ΔQ can also replace Q.

ΔT is T₁-T₂, where T₁ is the initial temperature, and T₂ is the final temperature of the substance. Begin by noting down the initial/starting temperature T₁ using a thermometer. Also, weigh the sample (m) and note the value in kg for later use.

Next, supply a known quantity of heat energy (Q) to the system. The quantity of heat energy can be noted in either joules or calories. Once you’re done supplying heat, wait for the temperature to stabilize and note the final temperature as T₂.

Convert the temperature value to Kelvin by adding the number 273.15 to the Celsius value (0°c = 273.15 K). If the value of heat energy supplied is available in calories, convert it to joules. Multiply the amount of heat energy in calories by 4.184 to get the amount in joules (1 cal = 4.184 joules).

Finally, substitute the values of Q, T₁, and T₂ in the heat capacity formula. Grab a calculator or use your brain to perform the calculations and obtain the sample’s heat capacity. The units of heat capacity are J/K.

Step 2: Finding Specific Heat Capacity Or Specific Heat

Specific heat capacity or specific heat can easily be found by dividing the sample’s heat capacity by its mass (c = C/m). Go ahead and divide the value of C found in the previous step by the value of m, also noted in the previous step, to obtain the specific heat of the sample. The resulting quantity will have the units J/kg.K

Step 3: Determining Molar Heat Capacity

If you scroll back up and look at the formula for molar heat capacity (c_m= C/n), you will find the term ‘n’, representing the number of moles of the sample. To find the number of moles, divide the quantity of the sample by its molar mass.

Now that you have found n, substitute the value of heat capacity (C) and the number of moles (n) in the formula and calculate molar heat capacity.

Another method for determining molar heat capacity is multiplying the specific heat (c) of the sample by its molar mass (M). When doing this, be sure to convert the molar mass to kg/mol.

Alternative Method – Using A Calorimeter

Another method for determining the specific heat of a substance is the use of a calorimeter. A calorimeter is a scientific apparatus consisting of the following parts: an inner and outer vessel, stirrer, thermometer, insulating material, etc.

The inner vessel or cup contains the sample material whose specific heat is to be determined. It is placed in the middle of the outer vessel which is filled with water.

The procedure starts by noting the mass and initial temperatures of both the water and the sample substance.

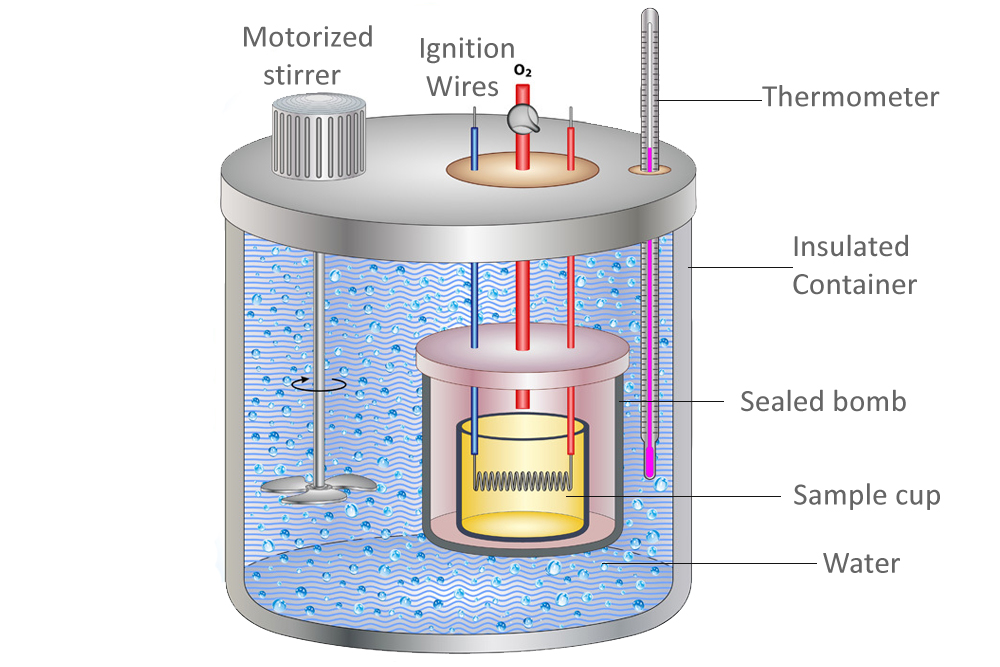
The sample is then heated using ignition wires. As the temperature of the sample rises above the temperature of the outside water, heat transfer between the two begins. After some amount of time, the electric flow is turned off, and the final temperatures of the water and the sample are measured. The heat energy lost by the sample material will be equal to the heat gained by the water in the outside vessel. We now make use of the formula ΔQ = mcΔT.

For the sample, ΔQ_s= (mcΔT)_s, and for the water, ΔQ_w=(mcΔT)_w.

But ΔQ_s = ΔQ_w. Thus, (mcΔT)_s = (mcΔT)_w.

Substitute the values for the mass of the sample and the water (m_s and m_w, respectively), the change in temperature (ΔT_s = T1_s-T2_s and ΔT_w = T1_w-T2_w), and the specific heat of water (c_w) as 4.1796 kJ/kg.K to determine the specific heat of the sample (c_s). Once the substance’s specific heat is found, multiplying it by its molar mass will provide you with the molar heat capacity of the substance.

Applications Of Heat Capacity

The heat capacity of a substance determines where and when it can be used. For example, the handles and handles of utensils are manufactured from materials with a high heat capacity to ensure the user’s safety. On the other hand, thermometers are manufactured from materials with a low specific heat capacity to detect even the smallest temperature fluctuations.

Another example of this is the use of water in engine cooling systems. Water has the highest specific heat capacity of all liquids. For the same amount of heat, the rise in water temperature is minimal, making it an ideal choice for a cooling liquid/agent.

The phenomenon of seawater remaining cooler than the surrounding air and sand on a hot summer day, even though it is exposed to the same amount of heat from the sun, can also be explained by the concept of heat capacity: the high heat capacity of water is responsible for many natural events, including the Earth’s climate and the survival of aquatic life!