Table of Contents (click to expand)
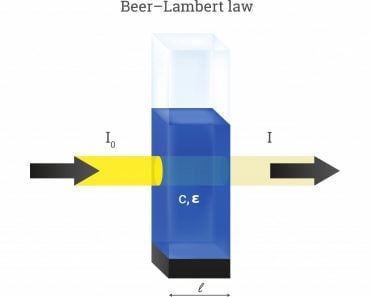
Henry’s Law is the mathematical relationship between the partial pressure of a gas and the concentration of that gas in a solution. The law states that the amount of gas that dissolves in a solution is proportional to the partial pressure of that gas.
It’s true that equations about mathematics can turn out to be extremely dry and mundane. They can sometimes lead to such a high level of abstractive thinking that these concepts and equations lose any kind of correlation to the real world. This is especially true of Henry’s Law, as it is highly abstractive. However, there is a reason it is called a ‘Law’, namely because it explains the phenomena of nature in the most scientific and mathematically precise way. Now, let’s try to establish a basic understanding of Henry’s Law.
Recommended Video for you:
Theoretical Understanding
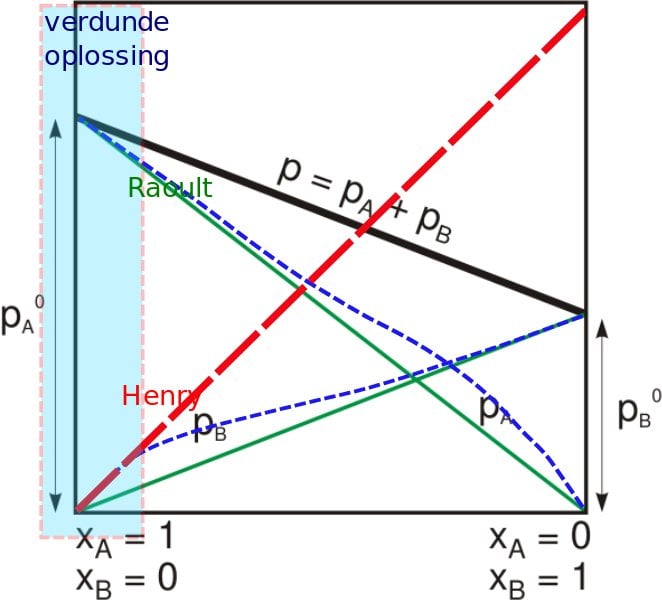
When gas comes in contact with the surface of a liquid, the amount of gas that will go into the solution is proportional to the partial pressure of that gas. For analysis, let’s assume some gas and the liquid to be water. The amount of the gas that dissolves at a particular temperature depends on the partial pressure that the gas exerts on the liquid. One simple thing we must remember is that the dissolved gas and the undissolved gas are in equilibrium. A simpler rationale for Henry’s Law is that if the partial pressure of a gas is twice as high, then on average, twice the number of gaseous molecules will hit the surface of the water. For a gas mixture, Henry’s law helps to predict the amount of gas (or even multiple numbers of gases) that will go into solution, but different gases have different solubility levels, which also affects the rate.
The Equation
Now that we have an understanding of a single broad application of Henry’s Law, let’s take a more rigorous mathematical approach to the understanding of Henry’s Law. A gas and a liquid will reach some equilibrium relationship.
Liquid ⇔ Gas
CsHe = Pi
The different elements are symbolized by the following abbreviations:
Cs = saturation concentration
He = Henry’s law coefficient
Pi= partial pressure of the gas
The standard unit for the Henry’s Law Coefficient (He) is expressed in terms of atm⋅m3/mole; P is in terms of atm, and for the saturation content, Cs is in mole/m3. The greater Henry’s Law coefficient, the greater the volatility and the less solubility. It is valid for diluted solutions and non-reacting gases at near ambient pressure and temperature. Ionic strength increases Henry’s coefficient and decreases gas solubility.
Dissolved Oxygen In The Water And Equilibrium
We will consider a very practical example, so that we can understand the physical relation of the above-mentioned equation with the real world. Let’s take a specific case of oxygen dissolving in water. Now, the oxygen that is dissolved has come into existence primarily for two reasons. The first reason is that it is the byproduct of photosynthesis of aquatic plants. The second is through direct absorption from the atmosphere.
For the oxygen concentration of water to be in equilibrium with the atmosphere, the concentration can be calculated with Henry’s Law. The equilibrium constant for O2 is 769.23. The equilibrium constant of oxygen in water is 0.00027. This is the equilibrium constant only at the surface of the water. Water below the air/water interface is not necessarily in equilibrium with oxygen in the atmosphere and can contain equilibrium constants different than what is indicated. It is a known fact that the oxygen concentration at the surface of lakes and oceans is higher than at greater depths. An important thing to know about the oxygen/water relation is the percentage saturation. Percentage saturation is the amount of oxygen that one liter of water can hold relative to the total amount of oxygen that water can hold at that temperature.
Running water in shallow streams has a better concentration of oxygen than still water, as it can mix well with the air. There is also a strong dependence between temperature and oxygen concentration. Atmospheric pressure is lower at higher altitudes, so water at higher elevations holds less dissolved oxygen than the water at sea level. The amount of dissolved oxygen is highest during the day time, as this is when photosynthetic organisms produce oxygen. As the temperature of water rises, its ability to dissolve oxygen into itself becomes more difficult. This can especially prove dangerous for aquatic animals, as they are prone to lower oxygen levels during the daytime or during hot summer days. There are other applications of Henry’s Law, such as carbon dioxide saturation in water, and even calculations of oxygen in the human bloodstream. Henry’s Law proves that even the most abstract concepts have the most basic practical applications.