What Is Beer’s Law?

Beer’s law states that the light absorbance of a solution is directly proportional to the concentration of the attenuating species and the optical path length.

Not to disappoint you readers, but Beer’s Law has nothing to do with your go-to Saturday night beverage. It actually relates to the decrease in the intensity of light as it passes through a solution, such as beer.

It’s a common observation that when we direct a beam of light through a solution, its intensity fades. For example, as kids, when we directed our laser lights or flashlights through a glass of milk or juice, we could hardly see any light emerge on the other side of the glass. Another naturally observed example of this is the transmission of solar radiation (light) through the atmosphere. The intensity of solar radiation emitted by the sun weakens as it passes through Earth’s atmosphere, which is good news for us!

The intensity of the radiation decreases because solution particles absorb some of it, only allowing some portion to pass through. Beer’s law creates a relation between the light absorbance of a solution and its attributes.

Recommended Video for you:

History Of Beer’s Law

The law might have ‘Beer’ in its name, but it was actually red wine that led Pierre Bouguer to discover a key part of this law. Pierre Bouguer, a French mathematician, was sipping on red wine in 1729 on his vacation in Alentejo, Portugal when he came up with one-half of Beer’s Law. However, Johann Heinrich Lambert is often credited for the full discovery, even though he was just the one to quote it from Bouguer’s “Essai d’optique sur la gradation de la lumière”.

Lambert, in his book Photometria, stated that the light absorbance of a sample is directly proportional to the length or thickness of the sample (solution) that light passes through. More than 120 years later, in 1852, August Beer found another relation for the decrease in intensity of light. He stated that “the amount of light absorbed by a solution or absorbance of a solution is directly proportional to its concentration”.

Beer Lambert Law And Its Formula

Beer’s law is just the relation between the absorbance and concentration of a solution. The two laws, Beer’s Law & Lambert’s Law, are combined to give a common relation between the absorbance of a solution to its concentration and path length (thickness of the sample). The law is therefore called the Beer-Lambert Law, the Lambert-Beer Law, or the Beer-Lambert-Bouguer Law. However, for simplicity’s sake, it is often simply called Beer’s Law.

The Beer-Lambert Law states: The absorbance of a solution is directly proportional to the path length of the sample and concentration of the attenuation species in the solution.

(Note: Attenuation is the scientific term for the gradual loss in flow intensity when passing through a medium.)

In simpler words, as the concentration and path length of the solution increase, the absorption of incident light also increases.

The law is mathematically expressed as:

A ∝ l c

Here, A is the absorbance of the substance, l is the path length, and c represents the concentration of the attenuating species in the solution.

Upon removing the proportionality sign, a constant term called the molar attenuation constant or absorptivity is introduced to the equation.

Absorptivity is defined as the extent to which something (chemical species) absorbs energy (radiation) and is represented using the greek letter ε.

Beer Lambert Law In Terms Of Transmittance

A beam of light directed through a solution can undergo quite a few optical phenomena. These include reflection, refraction, scattering, interference, and absorption—or the light could simply get transmitted through without changing at all. However, much more often than not, the intensity of light will reduce when passing through something. Let’s assume the intensity of the incident beam as I₀ and the intensity as it emerges out from the other side as I. The decrease in the intensity of light is then given as:

ΔI = I₀  –  I

Here, ΔI is the decrease in the intensity of light.

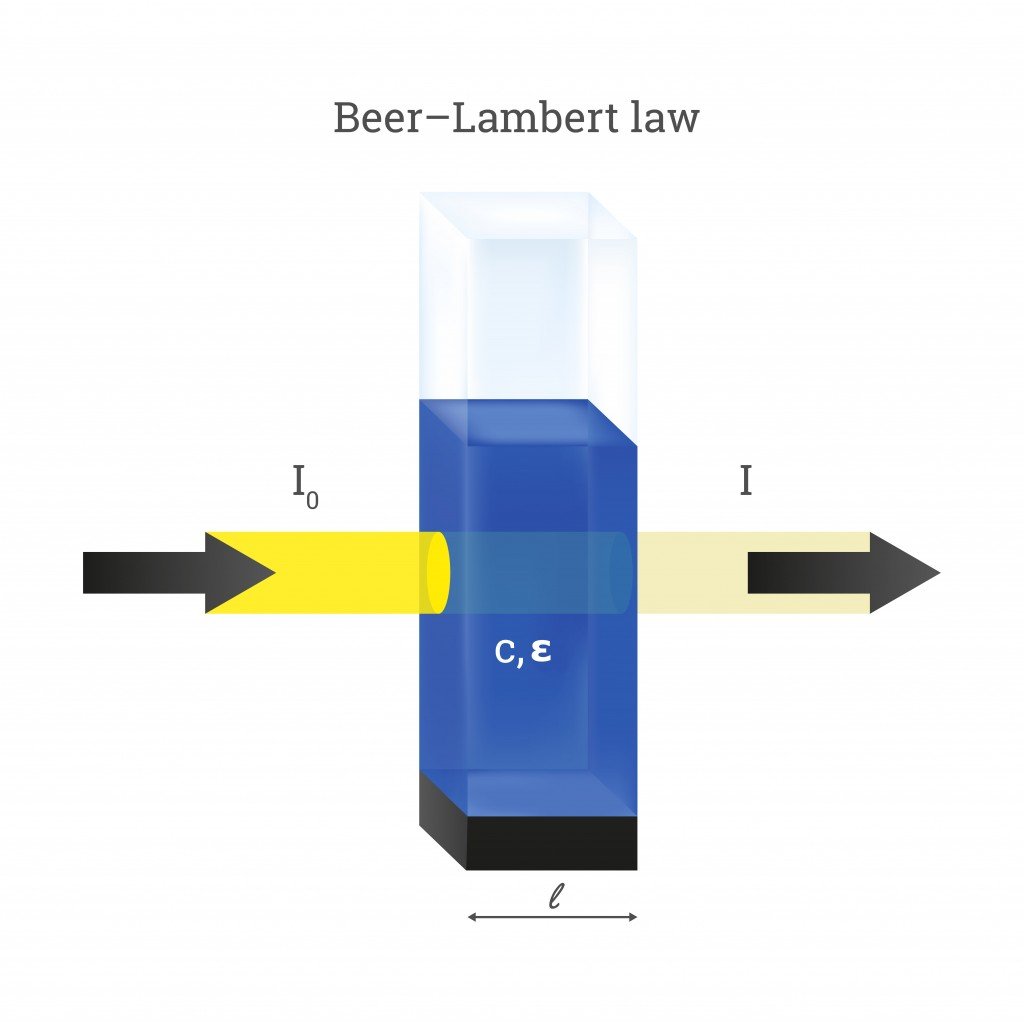
For the sake of Beer’s Law, let’s assume that the light only undergoes absorption and none of the other optical events. The value of ΔI then equals the amount of light absorbed by the solution (ΔI = I _absorbed). In reality, the amount of light absorbed is calculated by passing light through two different solutions—one that includes just the solvent and another with the solute (attenuation species) dissolved in it.

The values of I and I₀ help us find another important term called transmittance. We define transmittance as the amount of light transmitted (I) by an object compared to the amount incident light on it (I₀). Mathematically, transmittance (T) is expressed as:

On the other hand, the absorbance (A) of an object is defined as the log of the ratio of the intensity of incident light (I₀) to transmitted light (I). It is given as:

Combining the equations of absorbance and transmittance, we have:

Thus, the absorbance of a species is equal to the negative log of its transmittance (A = -log T). The Beer-Lambert Law can be expressed in terms of transmittance as:

The statement explaining Beer’s Law can also be modified to: ‘the amount of light transmitted through a solution remains constant if the product of concentration and path length remains constant’.

The equations A=εlc and T=10^-εlc are applicable when the solution has only one attenuating species present within it. A more generalized formula for N, the number of attenuating species in the solution, is given as:

Conclusion

Beer’s Law primarily finds applications in the field of spectrophotometry and the study of wave optics. Spectrophotometry involves passing a beam of ultraviolet or infrared light of a known wavelength through a solution. The amount of light absorbed and transmitted by the solution is then measured using an instrument called a spectrometer or colorimeter. Spectrophotometry finds importance in the testing of biochemical compounds, as the samples are available in limited quantities, so using non-destructive techniques becomes imperative.

However, Beer’s Law only works under specific conditions. Conditions in which Beer’s Law is not followed include: when the incident radiation isn’t monochromatic (single wavelength), when each incident radiation doesn’t traverse the same optical length, and in the case of higher concentration solutions.

Is Beer’s Law valid for beer? Well, now that you know all about the law, why not find out for yourself the next time you go out with your friends for a few weekend brews?