Fun Places To Hang Out In Space: What Are Lagrange Points?

Lagrange points are regions of equilibrium at which the combined gravitational field of two massive bodies is cancelled out by the centrifugal force felt by a third, much smaller object, such that the third object is at rest relative to the two large bodies.

“There is an art to flying, or rather a knack. The knack lies in learning how to throw yourself at the ground and miss. … Clearly, it is this second part, the missing, that presents the difficulties.”

– The Hitchhiker’s Guide to the Galaxy

About half a century ago, before people were considering terraforming Mars or the Moon for human habitation, another idea appealed to space settlement enthusiasts. The idea of space colonies emerged in the 1970s when physicist Gerard O’Neill put forth the concept of orbital habitats that would occupy relatively stable spots in space, called the Lagrange points.

So what are these Lagrange points and what makes them so important?

For starters, if you could aim for just the right spot between the Moon and Earth, one could place a relatively low mass object there, and it would stay there indefinitely, while going around Earth synchronously with the moon.

Recommended Video for you:

What Are Lagrange Points?

The gravitational forces exerted by two massive objects at a point are typically unbalanced, changing the orbit of any object located at that point.

However, Lagrange points are regions of equilibrium, at which the combined gravitational field of two massive (celestial) bodies is cancelled out by the centrifugal force felt by a third, much smaller object, such that the net force on the third body is zero.

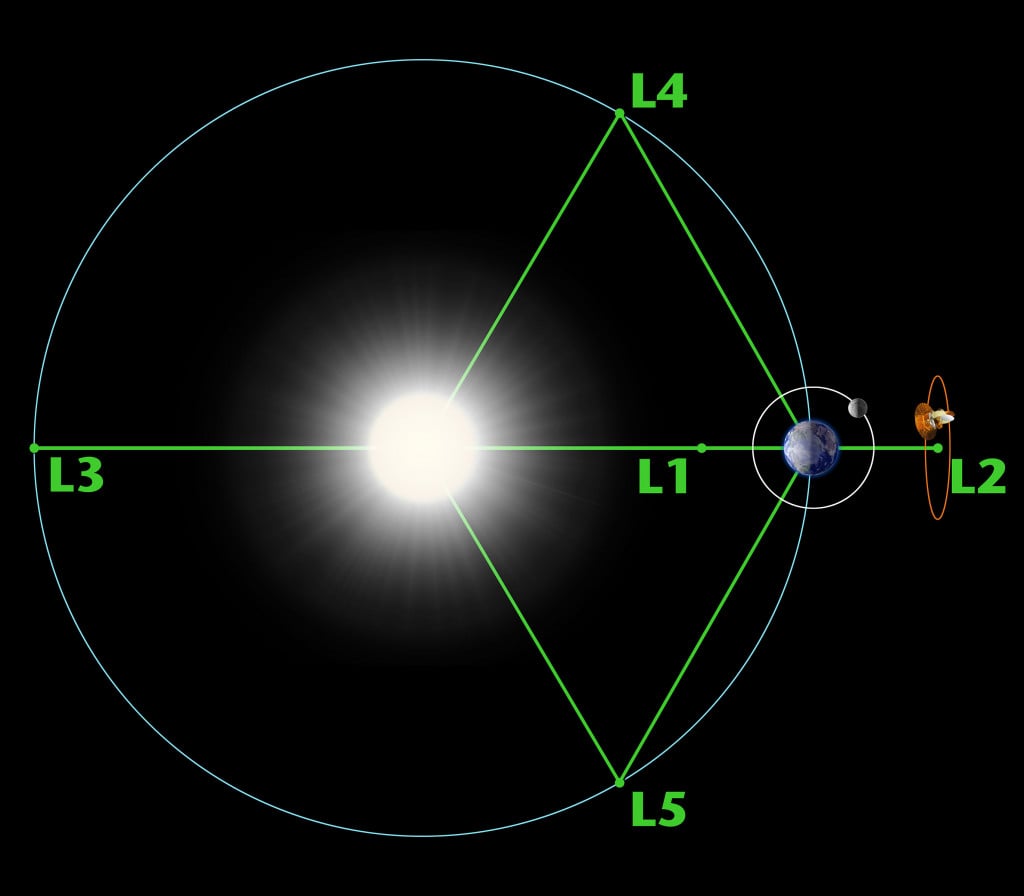
Therefore, once placed at an equilibrium point, the relatively low mass object would have zero mass and acceleration (relative to the heavier bodies), i.e., it would be at rest. There are five points around a star or a celestial body at which all forces are in balance.

Also called Libration points, these locations aren’t fixed in space, but are fixed relative to the two primary bodies. For the Earth-Moon system, the points move along with Earth-Moon’s center of gravity with the same period as the moon.

Math That Helped With The Three-body Problem

As long as it is just the Earth and the Moon careening towards each other, the Moon would continue to move along a very specific path that can be described mathematically with great accuracy. But what happens when a third body is added to this mix?

The three-body problem deals with calculating where three celestial bodies interacting through gravity (inverse square force) are located, with respect to each other, over time (i.e., motion). However, since space isn’t empty, and everything is being acted upon by several forces all at once, a system comprising three bodies is ultimately chaotic and the exact behavior of the bodies cannot be predicted.

While Newton was able to find a general solution for the two-body problem, solving the three-body problem proved a far more difficult task. When a third body came into the picture, the problem became much more complex. Research by Poincare indicates that a deterministic solution for the three-body problem may not exist.

However, gravity weakens with distance, i.e., gravitational force is dominant for bodies that are closer than for those far away. This principle has been used to create simplified models, such as the restricted three-body approximation, in which all other bodies except the two massively dominant masses in a system are ignored.

Lagrange points are spe­cial solu­tions of the restrict­ed three-body prob­lem in which one of the bod­ies is extremely small, in com­parison to the oth­er two.

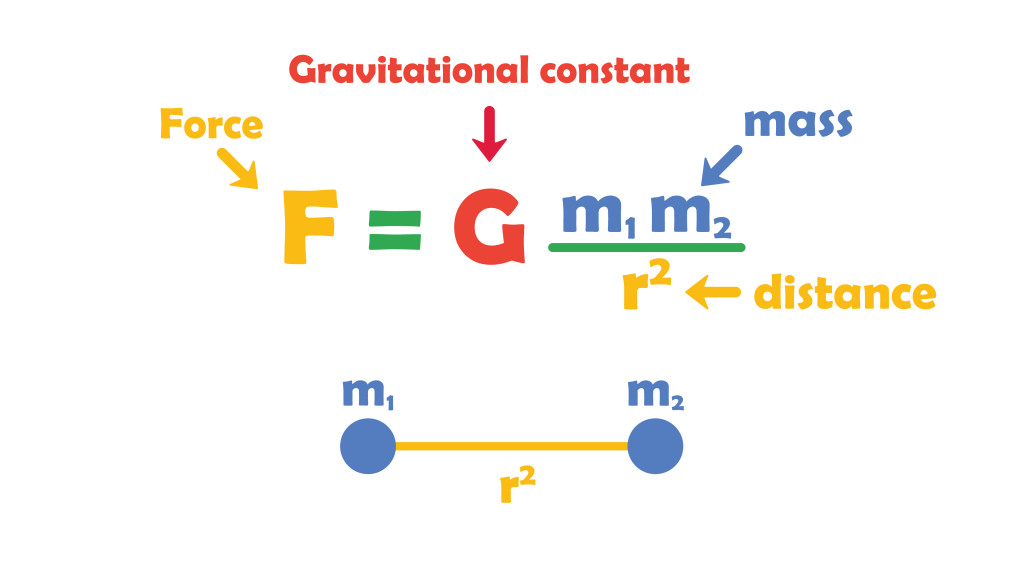
Since the Earth is more massive than the Moon, the gravity exerted by the Earth on other objects is stronger than that of the Moon. A third body (having negligible mass as compared to the primary bodies, such that its influence on the motion of the two other bodies can be neglected) placed between these two primary bodies will be acted upon by the forces exerted by both of them.

For example, a rock between the Earth and the Moon is drawn towards the Earth due to Earth’s mass, while it is also experiencing gravity’s pull from the Moon. The Earth, being much larger, is tugging at the rock with a greater force, but since the magnitude of gravity falls rapidly with distance, the farther the rock moves from the Earth, the smaller this pull becomes.

There comes a point at which the pull from Earth is equal to the pull from the Moon and the rock will experience zero net gravitational force. This point, called a Gravity Neutral Point, is the point at which an object having no velocity will stay and fall neither towards the Earth nor the moon.

Any closer to the Moon beyond this point and lunar gravity will dominate; the object will be pulled towards the Moon. Travel further away from this point and the object will be pulled back towards Earth.

The gravity neutral point is sometimes, erroneously, referred to as a Lagrange Point (more specifically L1). This confusion arises because the existence of a neutral point, in theory, carries the presupposition that the two bodies it is being defined for, are static, i.e., it is assumed here that the Earth and Moon do not move in the vacuum of space.

This, however, is not the case at all! The Earth and Moon orbit their common center of gravity and are constantly moving, due to which there is centrifugal force involved. (Basically, what the centrifugal force does is slingshot the object off into space as it moves around in its orbit).

Since both the Earth and Moon are moving, there are actually five different locations at which the interaction of gravity and the centrifugal force creates a point of equilibrium. In fact, for each system of 3 bodies where m3<<m1, m2 and m3<<m2<m1, five associated Lagrangian points can be found. There are five Lagrange points for the Earth-Moon system, and five for the Sun-Earth system.

L1, L2 and L3 are collinear (falling on a straight line). L1 lies between the two bodies; L2 lies on the same line, but beyond the smaller of the two bodies. L3 also lies on the same line, but is behind the larger of the two objects. L4 and L5 lie at the third vertex of the equilateral triangles whose base joins the two main masses of the system.

Gravitational Sweet Spots Of The Earth-Moon System

Let’s consider the Earth-Moon system again. Three out of the five associated Lagrange points lie on the Earth-Moon line (connecting the centers of Earth and the Moon). The first point, L1, lies between Earth and the Moon, where the combined effect of the gravitational pull of the two bodies produces an equilibrium, albeit slightly closer to Earth than the Gravity neutral point.

L2 lies further out in the direction of the moon, beyond its far side (the side facing away from Earth), while L3 can be found on the opposite side, lying far beyond Earth. For L2 and L3, effective forces (the pull of Earth’s gravity and the moon, centrifugal) cancel out, and an object placed at either location can go around the Earth in the same amount of time as the Moon.

L4 and L5 each represent the third vertex and the apex of the two equilateral triangles formed with the centers of the Earth and the Moon.

Are All The Points Stable?

Not all the equilibrium points are stable. L4 and L5 points remain stable, so long as the mass ratio between the two large bodies exceeds 24.96, a condition that is satisfied for the Earth-Sun and Earth-Moon systems, as well as the Sun-Jupiter system. Since the Earth is approximately 81 times the mass of the Moon, and the Sun is over 1000 times the mass of Jupiter, the L4 and L5 points of the Earth-Moon and Sun-Jupiter rotating systems are stable.

The L1, L2 and L3 points are intrinsically unstable. Stationing an object at these points is somewhat similar to balancing a ball on a hill. Place an object at precisely the right point and it will stay put. However, the slightest disturbance will sway it from its position, making it eventually drift. An object placed at any of the unstable points will therefore need assistance to remain in the “sweet spot”.

​If an object is not located at the exact point where all forces cancel, then its position will be destabilized and it will oscillate (orbit) around the point of equilibrium in paths known as librations. Each Lagrangian point is surrounded by an extended region where a body can stick around with a little station keeping, i.e, a spacecraft orbiting a certain Lagrangian point really means that it is traveling within one of these extended, “island orbits”. The size of each island varies.

Space Missions At Lagrange Points

The SOHO (Solar Heliospheric Observatory) Advanced Composition Explorer (ACE), and the Global Geoscience WIND have been in orbit around the Sun-Earth L1, which affords constant and uninterrupted observation of the Sun, making it an ideal location for studying the solar environment. Unlike SOHO, the solar observatories that had previously been orbiting Earth had their observations interrupted whenever Earth eclipsed the Sun, obscuring the field of view of the star.

The (WMAP), which was deployed to determine conditions in the early universe from the data collected on cosmic microwave background radiation, was positioned near the Sun-Earth L2 (2001-2010), but rather than staying at L2, it followed a lissajous pattern around the equilibrium point. (libration)

The JWST (James Webb Space Telescope) at the Sun-Earth L2 and DSCOVR (Deep Space Climate Observatory) at L1, can be maintained there with minimal fuel consumption and minor adjustments. Several other space observatories, such as the Herschel and Planck (to measure CMB with extreme precision), and Gaia (to map the positions and velocities of one billion stars to study the history of the Milky way), also orbit the Sun-Earth L2.

Lagrangian Prisons

For the Sun-Jupiter sys­tem, over 7,000 asteroids cluster around the gravitationally stable L4 and L5 Lagrange points. Called Trojans, these asteroids are broadly grouped into two swarms – one preceding and the other following the gas giant as it orbits the Sun.

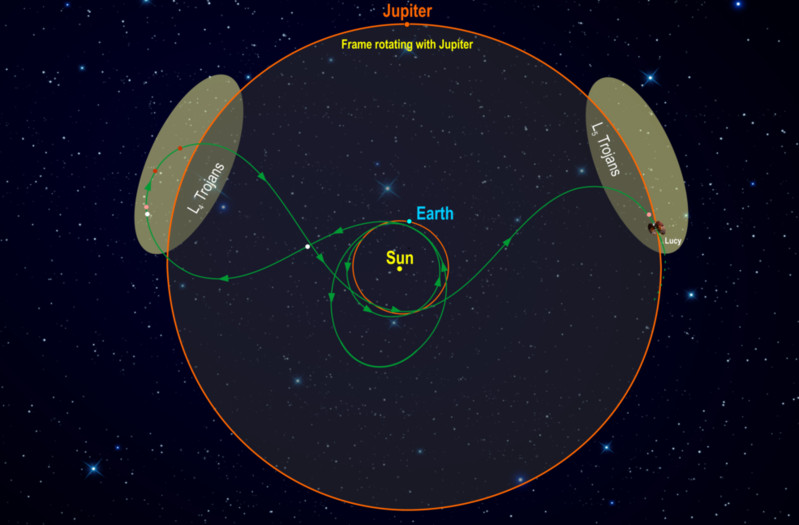
Scientists have suggested that Lagrangian regions may trap yet to be discovered planetary bodies or even debris from ancient extra-terrestrial spaceships. Since Lagrange points occur in space where two or more opposing forces are balanced, if a spacecraft could generate a force to counteract gravity, it would be possible to create artificial equilibrium points in space so that a spacecraft could hover almost anywhere in space without having to constantly follow a certain orbit. Solar sails that use sunlight for propulsion could be used for this purpose.

Undoubtedly, missions to Lagrangian sites could be used as stepping stones on the way towards much deeper space exploration.