Coefficient Of Restitution: Definition, Explanation And Formula

The coefficient of restitution is defined as the ratio of the final velocity to the initial velocity between two objects after their collision. Another way of saying this is that the coefficient of restitution is the ratio of the velocity components along the normal plane of contact after and before the collision.

The coefficient of restitution is defined as the ratio of the final velocity to the initial velocity between two objects after their collision. Another way of saying this is that the coefficient of restitution is the ratio of the velocity components along the normal plane of contact after and before the collision.

We made a 5-minute video on the coefficient of restitution and its applications in everyday lives. Check it out here:

There are some things that are very bouncy, and then there are things which are absolutely the opposite. For instance, if you bounce a rubber ball on a wooden floor, you know it will bounce back to your hands. But try bouncing a heavy, metal ball on the floor. Not only will you not get the ball back in your hands, but it’s very likely that you might have to spend a lot of money on the repair of your floor. So, don’t try this at home!

Let’s talk about the coefficient of restitution now, shall we?

As its name signifies, the coefficient of restitution is actually a measure of the “restitution” (i.e., what you give back) of a collision between two objects, or in other words, how much of the kinetic energy remains after two objects collide.

If you happen to be a physics enthusiast, you probably understood the aforementioned description of the coefficient of restitution, but if physics isn’t your strong suit, let me take a few steps back and give you a bit of ‘background’ about this fairly complex-sounding entity.

Recommended Video for you:

Coefficient Of Restitution: A Simple Explanation

When two objects collide with each other, many forces come into play, which also means the application of various mathematical equations. Many of these laws were first derived by the same super popular scientist who is credited with numerous discoveries and derivations, meaning that he has a number of patents to his name – Sir Isaac Newton.

Pertaining to the collision of two objects, Newton formulated a theory that we now know as Newton’s law of restitution. It simply states that when two bodies collide, the speed with which they move after the collision depends on the material from which they are made.

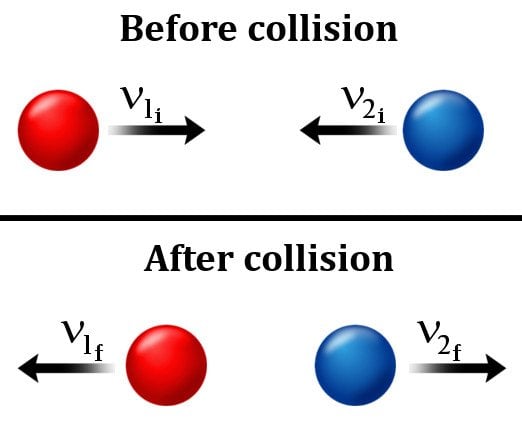
Let’s suppose a rubber ball bounces on a flat, hard surface. Obviously, the rubber ball will rebound off the surface, but with only a fraction of its original energy, because all real collisions are inelastic. (Note: If this collision were elastic, then the ball would have bounced back with the same amount of energy it had before striking the surface.)

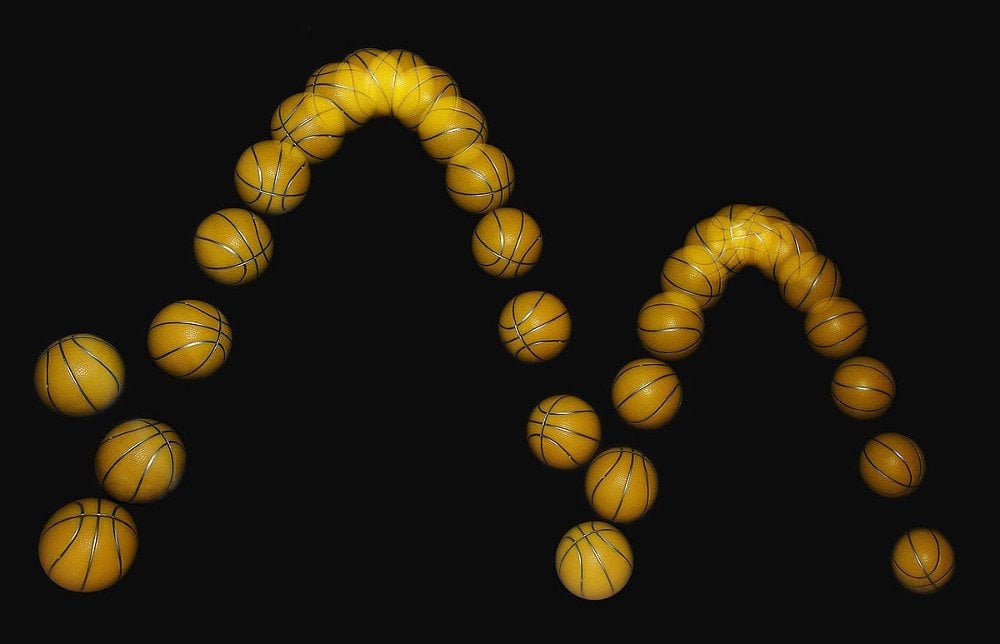
You see, when you ‘deform’ something by colliding it with something else (say, when you bounce a basketball on the ground), a fraction of its original energy is lost. That’s why the basketball bounces lower with every collision – as its energy gets converted to heat/vibrations.

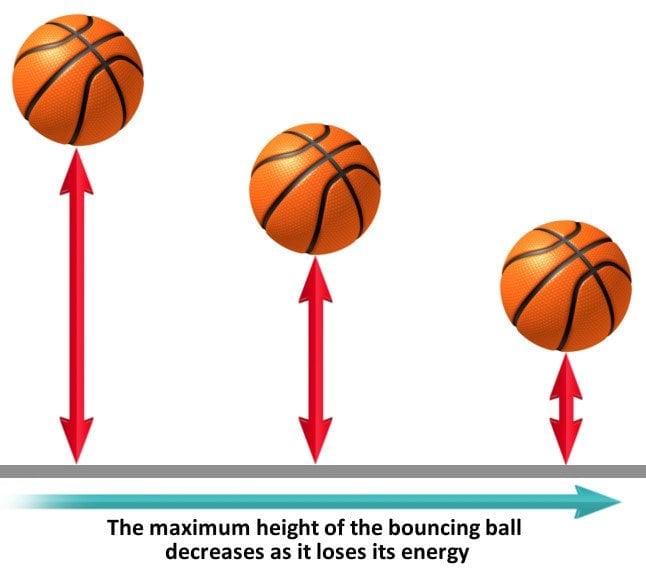
In this case, you can think of the coefficient of restitution as an entity that tells you how efficient the “bouncing” process is. The more efficient it is, the more ‘bouncy’ the basketball shall be.

Values Of The Coefficient Of Restitution

As mentioned earlier, the coefficient of restitution is a measure of how much kinetic energy remains after the collision of two bodies. Its value ranges from 0 to 1. If it’s on the higher side (i.e., close to 1), it suggests that very little kinetic energy is lost during the collision; on the other hand, if the value is low, it indicates that a large amount of kinetic energy is converted into heat or otherwise absorbed through deformation.

In the case of a perfectly elastic collision, which does not happen in real-world settings, the coefficient of restitution would be precisely 1.00. Therefore, if you want a basketball that’s more ‘bouncy’ than others, you need to pick one with a high coefficient of restitution.

Coefficient Of Restitution Formula

The formula to calculate the coefficient of restitution is rather straightforward. Since it is defined as a ratio of the final to  the initial relative velocity between two objects after their collision, it can be mathematically represented as follows:

When considering a one-dimensional collision of two objects, A and B, the coefficient of restitution could be calculated by:

In the case of a ball bouncing off a flat, stationary surface, the coefficient of restitution turns out to be:

These formulas could be used to calculate the value of the coefficient of restitution with different available variables.