Table of Contents (click to expand)
Yes, doubling the speed of a vehicle on a highway only doubles the impact force of an accident.
We’ve all seen the Hollywood blockbusters like Bad Boys 2 and the Fast and the Furious franchise, so we know a good car crash when we see one. However, in real life, car accidents cause major loss of life and are extremely costly all around the world!
Millions of car accidents happen on this planet, ranging from fender benders at stoplights to huge pileups on highways on the slippery roads of winter. You’ve probably seen or heard of hundreds of car accidents in your life, and may have even been involved in one yourself.
One thing I always notice is how much more serious highway accidents seem to be versus urban accidents. They’re both terrible, don’t get me wrong, but highway crashes seems to be much more devastating than urban accidents.
Why is that?
Recommended Video for you:
As Always… Physics Comes Into Play
Whenever we talk about moving objects, from galaxies billions of light years away to a marble moving across a table, the language we use is physics. Therefore, when discussing car accidents, there’s no way to avoid doing a bit of math – or at least understanding some!
When you are driving a car, you are moving forward at a certain velocity due to varying acceleration and braking. Therefore, a car accident of any kind is primarily concerned with Newton’s Third Law of Motion and the work energy principle. The amount of force that your car and body experiences based on these laws and principles determines how much danger you are in.
Newton’s Third Law states that for every action, there is an equal and opposite reaction. When you punch a concrete wall, it hurts your hand because essentially, the concrete wall punched back!
On a related note, the work energy principle states that the work done on an object is equal to its change in it’s kinetic energy. When the wall changes the amount of energy of your fist moving forward, it does an equal amount of “work” on your knuckles.
Now, when we apply these broad concepts to a moving car hitting an object (another driver, a median, a light pole), we start to understand just what a car accident can do.
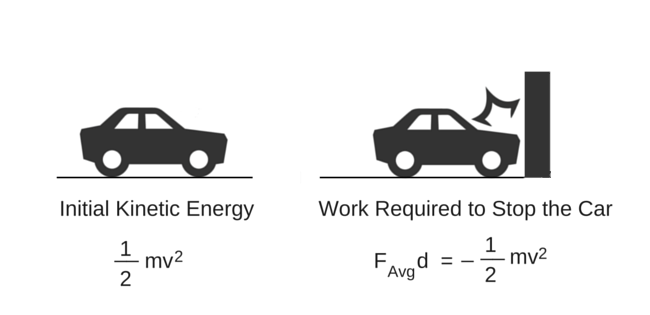
To analyze this example, first we need to consider the kinetic energy with which the car is moving. The equation for kinetic energy for the car is:
The object stopping this car will have to do some work which should be equivalent to the Kinetic Energy of the car. Now if the car stops at a distance “d” (after the crash) then the equation for Force is:
When we plug in the variables of an average car, with a mass of roughly 1.6 tons, we find that a large amount of force is created even from slow-moving vehicles.
Imagine a car is moving at 30 mph (about 50 km/hr) and strikes a wall, crumpling and stopping after 1 foot. Let’s assume that the car weighs 3200 pounds (about 1450 kgs). By calculating the initial kinetic energy of the car and the force required by a wall/tree/driver to stop a car, we find that the total force of that impact is roughly 48 tons per sq foot.
If you have a head-on collision with another car moving the same speed, but from the opposite direction, then the kinetic energy doubles (because the other car also has the same kinetic energy) and thus the force doubles. In that case the total impact is roughly 96 tons per sq ft.
The Highway Is A Dangerous Place
When you are driving in an urban or residential area, you rarely see a speed limit over 40 mph (about 60 km/hr), which helps to cut down on accidents and accident severity. When we are moving slower, and typically in more slow-moving traffic, our reaction times don’t have to be as fast, and we are more engaged due to constant activity (stoplights, signaling, reading street signs etc.)
On a highway, when speed limits climb up to 80 mph (about 130 km/hr), the potential for danger is far greater. Not only do the higher speeds reduce the amount of reaction time a driver has, but there are also other hazards. Long-distance drives on highways (sometimes poorly lit ones) often result in tiredness, drifting into other lanes, smashing into medians, poorly navigating construction sites, and even suffering head-on collisions with other drivers that may be dealing with the same challenging variables on the road.
Now, imagine that earlier calculation in a much faster setting. Perhaps you are cruising across the country at 75 mph (about 120 kh/h) and your eyes begin to droop. You don’t notice the sharp turn coming up ahead, and your foot remains on the gas pedal. You crash directly into the concrete corner along the curve.
Now, applying the same calculation as above, although the speed is roughly double, the total impact force is roughly 300 tons per square foot – approximately 6 times more destructive!
For one final example, imagine you are speeding along the highway at 75 mph, your car drifts into the opposite lane, and smashes head-on into a car going the same speed. The results are truly terrible, and as before, the impact force doubles, because the opposing car has an identical forward force.
That means an impact force of roughly 600 tons per square foot! Compared to a head-on collision at 30 mph, the force is once again 6 times greater, and exponentially more devastating for everyone involved.
Because the equation of kinetic energy squares the velocity, the total impact increases significantly as compared to the previous example. Although the speed is only 2.5 times more than our 30-mph example, the force experienced by the car and the driver is 6 times greater. That is why highway collisions (head-on or otherwise) are so much more disastrous than urban fender-benders or 30-mph crashes into light poles.
To put that in frightening perspective, it only takes 3300 newtons (roughly .34 tons of force) to break a rib. Imagine the impact of 600 tons of force!
Perhaps now you understand why there is a slow lane on the highway! Some people aren’t in that much of a rush, and they choose to stay safe by driving slow. Speed is a powerful thing, which can make highway crashes truly terrible things to witness – and experience!
