Table of Contents (click to expand)
Tangential velocity is the component of motion along the edge of a circle measured at any arbitrary instant. Tangential velocity describes the motion of an object along the edge of this circle whose direction at any given point on the circle is always along the tangent to that point.
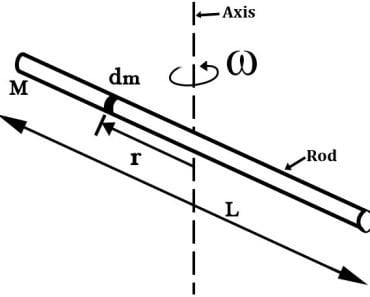
The tangential velocity is measured at any point tangent to a rotating wheel. Thus angular velocity, ω, is related to tangential velocity, Vt through the formula: Vt = ω r. Here r is the radius of the wheel. Tangential velocity is the component of motion along the edge of a circle measured at any arbitrary instant. As the name suggests, tangential velocity describes the motion of an object along the edge of this circle whose direction at any given point on the circle is always along the tangent to that point.
Jumping off a moving bus is dangerous, and so the conscious decision to make the jump evokes a sense of thrill. Jumping off the edge of a swirling carousel is the 9-year-old version of it unless you have a sibling who voluntarily gives you a This-is-Sparta-esque kick and sends you flying off into oblivion.
Besides habitually derailing from what is important and unnecessarily sharing what I deem as my life-changing traumas, I also possessed more of something known as tangential velocity. Aha! So that’s what this article is about!
Recommended Video for you:
What Is A Tangent?
A tangent is simply a line that touches a function at only a single point. The term function here is used to define any non-linear curve. It represents an equation – a relationship between the coordinates “x” and “y” on a two-dimensional graph.
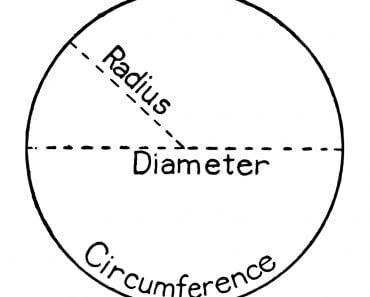
For instance, consider the curve that we’re most familiar with – the good ol’ circle. A circle is defined by the equation 
. This means that for a constant radius ‘r’, specific values of ‘x’ and ‘y’ trace out a splendid arc that like the end of a game of Snake meets its own end.
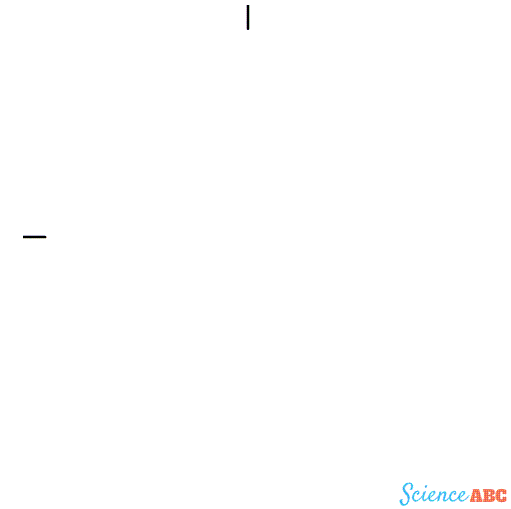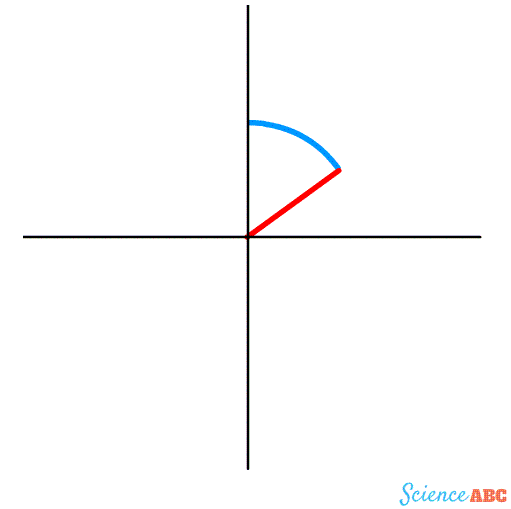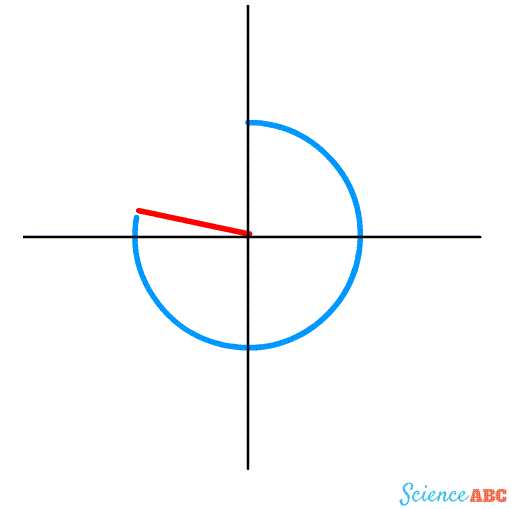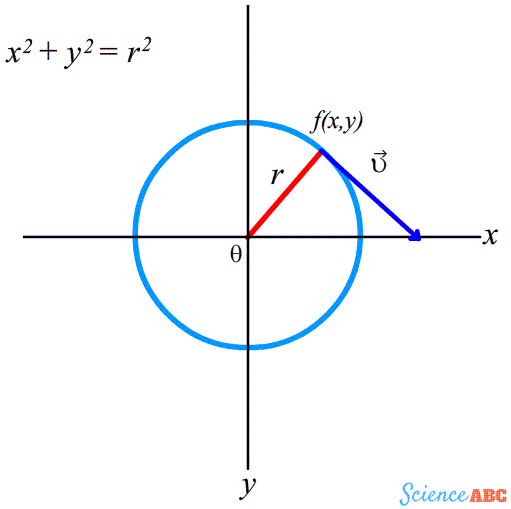
However, for simplicity, I’ve purposely considered an equation that describes an orthodox circle whose center lies on the origin — the reference point or the coordinates (0,0), and where ‘r’, the radius, is the distance from the origin to the edge of this circle.
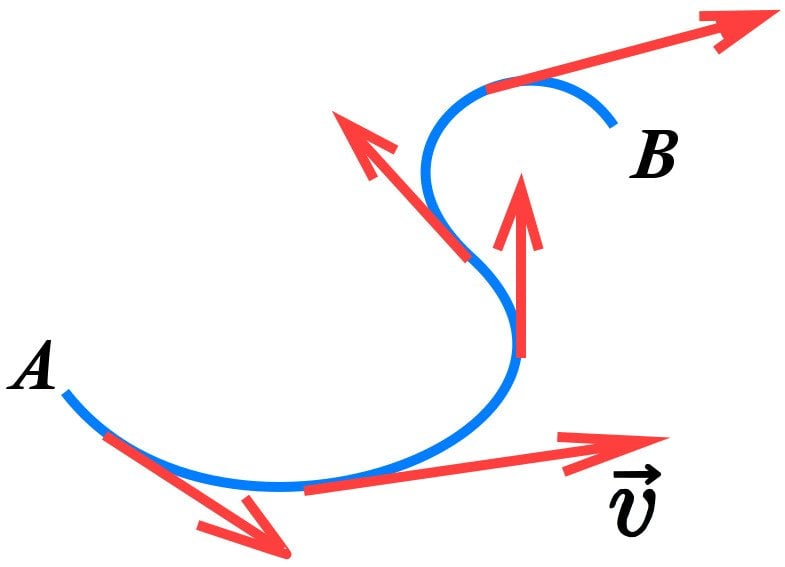
As the name suggests, tangential velocity describes the motion of an object along the edge of this circle whose direction at any given point on the circle is always along the tangent to that point. However, the concept is not restricted to just uniform circular motion; it also applies to all non-linear motion. If an object moves from Point A to Point B through a non-linear curve, then the red arrows represent the tangential velocity 
at various points on this trajectory.
Let’s stick to the circle for now.
The Formula For Tangential Velocity
First, we calculate the angular displacement, ‘q’, which is the ratio of the length of the arc ‘s’ that an object traces on this circle to its radius ‘r’. It is the angular portion under the arc’s shadow, between the two lines originating from the center and connected to its ends. It is measured in radians.
The rate of change of an object’s angular displacement is called its angular velocity. It is denoted by ‘w’ and its standard unit is radians/second (rad/s). It is different from linear velocity, as it only deals with objects moving in a circular motion. Basically, it measures the rate at which angular displacement is swept.
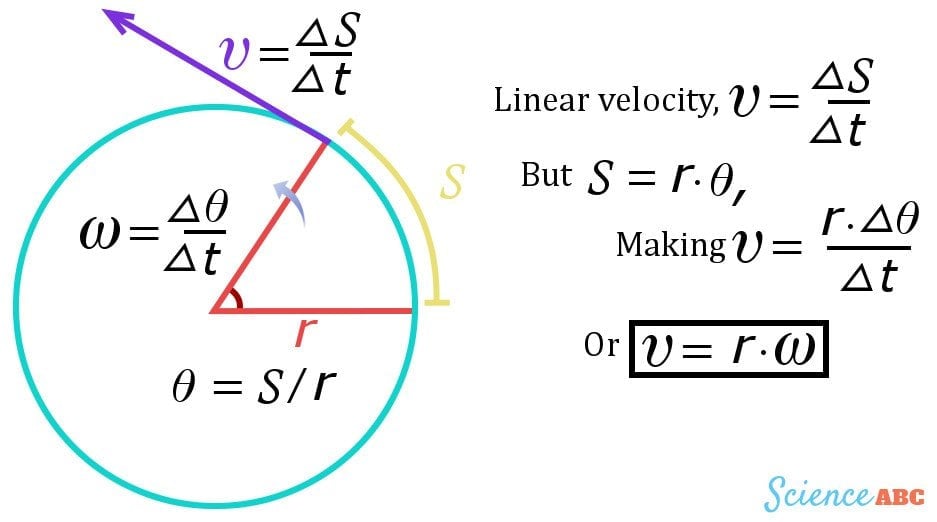
The linear component of angular velocity is known as linear velocity, which is the rate of change of an object’s linear displacement. Linear displacement is the arc ‘s’ cited above – the length of the arc. The rate of change of the product of radius ‘r’ and angular displacement ‘q’ is the object’s linear velocity. The radius is excluded from the operation, as it is a constant. We realize that the velocity is the product of the object’s angular velocity and the radius of the circle it traces.
The linear velocity of an object moving in a circle, measured at an arbitrary instant, is its tangential velocity itself!
Another way to define linear velocity is in terms of time period. If the time period is the time required by an object to go around the circle once, then the velocity at which it does so is ‘s/t’ (distance/time).
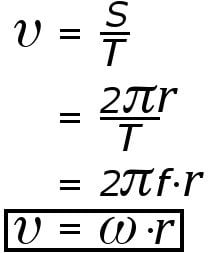
The reciprocal of ‘T’ is known as frequency and is denoted by ‘f’. This is the number of cycles achieved per second. The product of 2pf is known as angular frequency and is denoted by ‘w’, which helps us arrive at the previously derived result.
The Cross-Product
It is imperative to know that tangential velocity is a vector, that is, it has both size and direction. Vectors are indicated by an arrow above their standard symbol. Although their direction changes continuously, their total value remains the same. Each vector is a cross or the vector product of two vectors, which is the multiplication of their magnitudes and the sine of the angle between them. The resulting vector has a direction perpendicular to both involved vectors.
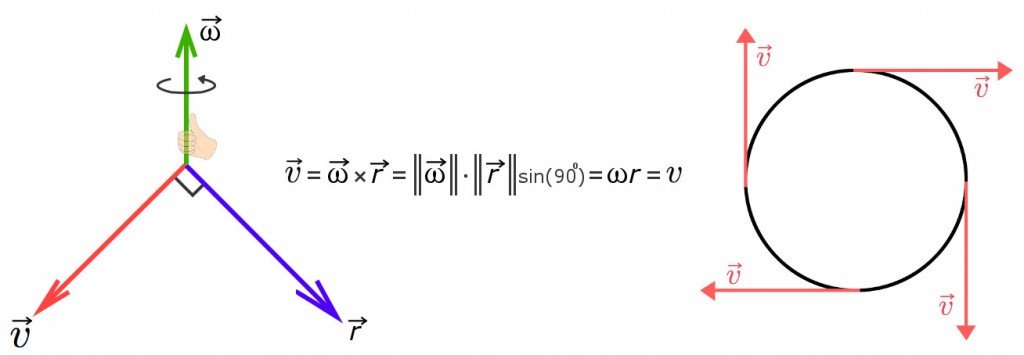
The two vectors whose product we require are the radius ‘r’ and angular velocity ‘w’. The right-hand rule states that if you hold the axis with your right hand and rotate the fingers in the direction of motion of the rotating body, then your thumb will point in the direction of the angular velocity, clearly implies that 
and 
are perpendicular to each other. And as the sine of 90 is one, the resulting perpendicular vector of these quantities at any point on the circle will always remain the same.
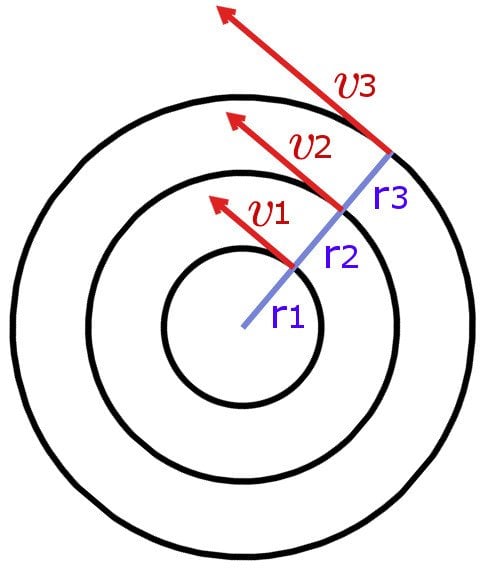
Interestingly, objects in or on the circle have the same angular velocity, but different tangential velocities. This is due to its dependence on the radius, as evident in its formula. Therefore, people at the rim of a merry-go-round would fly off at greater velocities than those seated deeper in it.
Importance Of Tangential Velocity
Tangential velocity can be observed in many cases, including any nonlinear motion, such as the abrupt jump from a swing or the deviation of a satellite or the Earth itself from its circular orbit. The circular motion of a satellite or our Earth occurs in an occult zone where the centripetal force that pulls it inward is offset by the linear velocity that pushes it straight forward.
However, when the Earth or the Sun suddenly disappears, we break our cycle and are instantly flung into space due to our linear speed. The motion draws a straight line through a point in space and time that marks the immediate instant where the pull of gravity disappeared – a tangent.
