Table of Contents (click to expand)
Inertia is the measure of resistance that a body of a certain mass offers when plunged into motion or, on the contrary, bought to a halt by an external force. Inertia, or the tendency of objects to resist change, varies with mass. Heavier objects are difficult to accelerate when at rest and equally difficult to stop when in motion, as compared to lighter objects.
The prefix ‘moment of’ in physics is used to depict the rotational counterpart of a linear quantity. Thus, the ‘moment of inertia’ is the rotational equivalent of mass for linear motion. It is denoted by ‘I’. Similarly, the ‘moment of force’ is the rotational equivalent of linear force, also known as torque.
Recommended Video for you:
How Do We Calculate Moment Of Inertia?
The moment of inertia ‘I’ of a rotating object with respect to its axis of rotation is given by the product of its mass and the square of its distance from the axis of rotation. However, this is only true for uniform or ordinary objects, such as an orb attached to a string whirling around at a certain angular velocity.
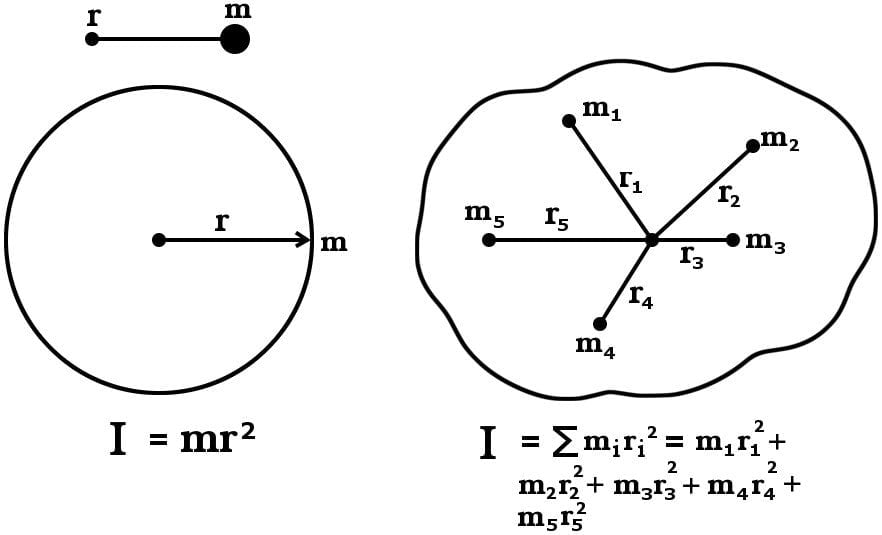
For non-uniform objects, moment of inertia is calculated by the sum of the products of individual point masses and their corresponding distance from the axis of rotation. This generalized relationship can be used to calculate the moment of inertia of any system, since any object can be constituted as an aggregation of similar point masses.
To calculate the moment of inertia of such a continuous distribution of mass at various distances, we use calculus, due to its dexterity with continuous variables.
We use a differential element of mass, an infinitesimal chunk of mass dm. The differential moment of inertia is then, dI = r²dm. To calculate the moment of inertia ‘I’ of the whole of mass ‘M’, we sum the differential moment of inertia dI contributed by dm throughout the surface. Or simply, we integrate.
Also Read: What Is Angular Momentum?
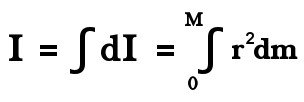
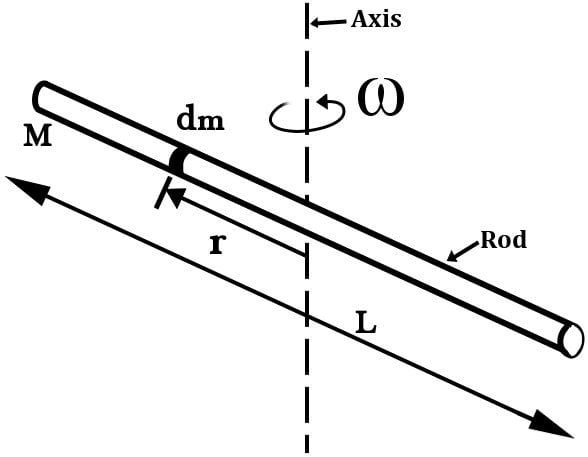
Moment Of Inertia Of A Rod
Consider a rod of mass ‘M’ and length ‘L’ such that its linear density λ is M/L. Depending on the position of the axis of rotation, the rod illustrates two moments: one, when the axis cuts perpendicular through the center of mass of the rod, exactly through the middle; and two, when the axis is situated perpendicular through one of its two ends.
Also Read: Mass Vs Weight: The Difference Between The Two
Axis Through The Center Of Mass
Similar to the infinitesimal element of mass dm, consider an infinitesimal element of length dl corresponding to it. Drawing the origin at the center of mass resting on the line of the axis, we realize that the distance of the rod to the left from the origin to its end is -L/2, while the distance from the origin to the other end to its right is +L/2.
Assuming that the rod is uniform, the linear density remains a constant such that:
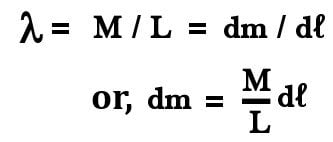
Substituting the value of dm in our expression to calculate moment of inertia, we get: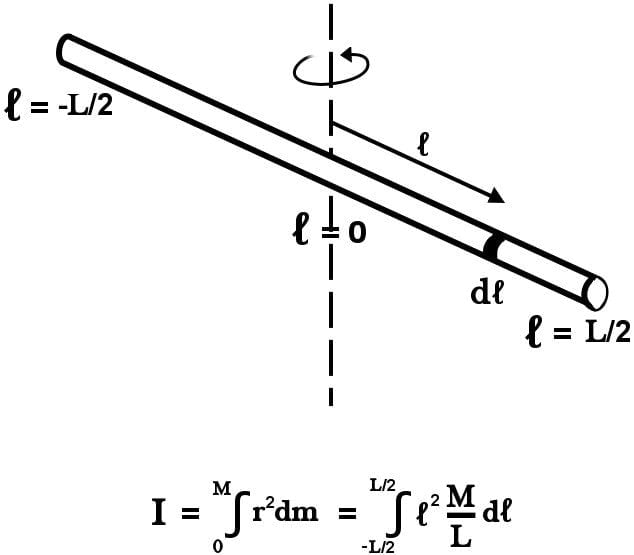 
Because the variable of integration is now length (dl), the limits have changed from the previously depicted M to a required fraction of L.
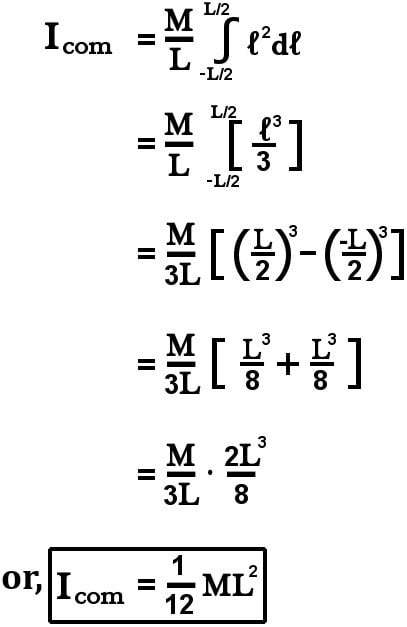
Axis Through An End
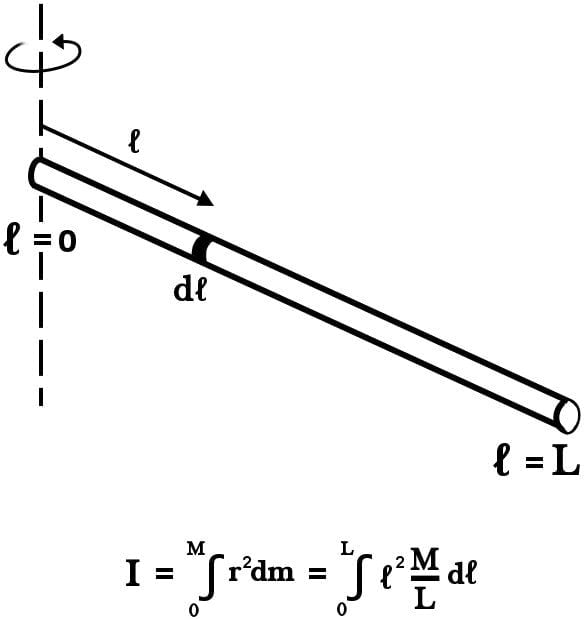
In order to calculate the moment of inertia of a rod when the axis is at one of its ends, we draw the origin at this end.
We are required to use the same expression, however, with a different limit now. Because the axis rests at the end, the limit over which we integrate is now zero (the origin) to L (the opposite end).
After integrating, we get:
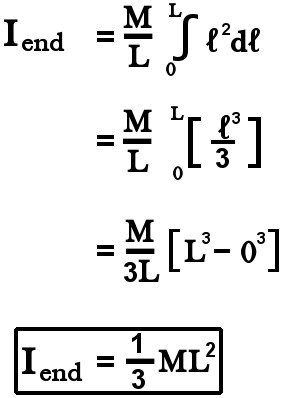
We can also arrive at the same result for the moment of inertia about the end by using the parallel axis theorem, according to which:
As L (com,end) is L/2, we find that:
This is in agreement with our previously derived result.
