Table of Contents (click to expand)
Centripetal acceleration is the acceleration towards the center of the circle while centrifugal force is the apparent force that seems to pull objects outwards. Centrifugal force is not a real force, but rather the result of inertia.
An acceleration, according to Newton’s second law of motion, is impossible to achieve without an object being subjected to a force. A body experiences centripetal acceleration when it is subjected to a centripetal force. However, unlike centripetal force, a centrifugal force is not real. Even though we experience this pair of forces almost every day, physicists deem the latter — in the jargon of physics — apparent. How is centripetal acceleration different from linear acceleration? Why is the centripetal force that imparts this acceleration considered real, while centrifugal force isn’t? Here’s how, and why.
Recommended Video for you:
What Is Centripetal Acceleration?
A body experiences centripetal acceleration when it is forced to travel in a circle, or at least in an arc. The force that causes it to do so is called a centripetal force. As the name suggests, the force is directed towards the center of the circle that the body traces or the center of the circle the arc would draw if it were allowed to be completed. For this reason, the centripetal acceleration imparted is also referred to as radial acceleration.
 A body traces a circle by changing its trajectory constantly, at every instant throughout its motion, and at each of those instants, it experiences centripetal acceleration. What is surprising is that a body experiences centripetal acceleration even when it is tracing an arc or a circle at a constant velocity. This is counterintuitive, as we typically define acceleration as a change in velocity. However, velocity is a vector, meaning that it exhibits magnitude as well as direction. Therefore, even though the body might travel at a constant velocity, it still accelerates because, at each point on the circle, it changes its direction.
A body traces a circle by changing its trajectory constantly, at every instant throughout its motion, and at each of those instants, it experiences centripetal acceleration. What is surprising is that a body experiences centripetal acceleration even when it is tracing an arc or a circle at a constant velocity. This is counterintuitive, as we typically define acceleration as a change in velocity. However, velocity is a vector, meaning that it exhibits magnitude as well as direction. Therefore, even though the body might travel at a constant velocity, it still accelerates because, at each point on the circle, it changes its direction.
At each point on the circle, the body is subjected to two accelerations, the directions of which are perpendicular to each other. One is the centripetal acceleration, directed towards the center or inward, and second is the linear acceleration, which is directed immediately forward of the body, or outward, but more precisely, tangential to the point of concern on the circle.
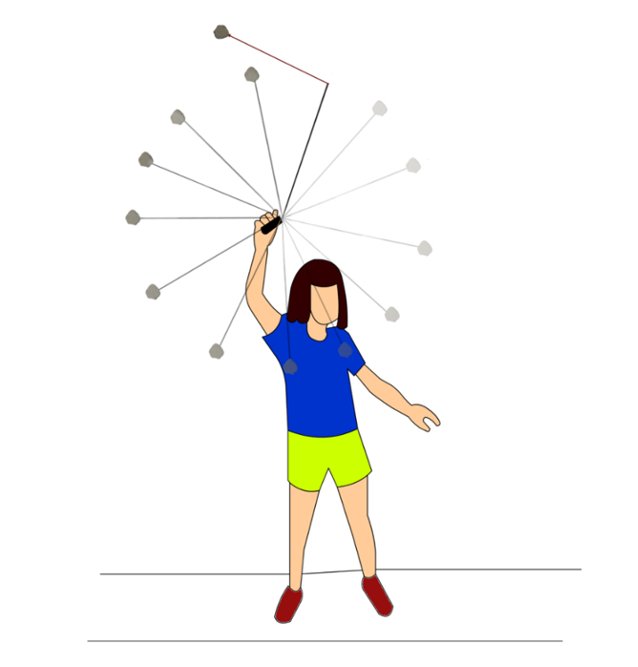
Consider the simplest example – a thread on one end of which you exert tension with your fingers that causes the stone attached to the other end to whirl around you. The stone’s centripetal acceleration is directed towards the center of the circle — that is, along the tension in the thread, towards your hand, the tension’s source — while the stone experiences linear acceleration when it is unleashed abruptly. You would observe that the stone is then hurled in a single direction immediately – the instant it is free of the centripetal force, its inertia forces it to move linearly – it then travels along the tangent drawn to that point in that very instant.
Centripetal acceleration is directed towards the center of the circle because the centripetal force that imparts it is directed towards the center. As demonstrated by Newton, a body accelerates in the same direction in which the force is applied. This is because it is in this direction in which the force causes the change in velocity. The diagram below illustrates this, and it is this diagram that we will use to derive the expression for centripetal acceleration.
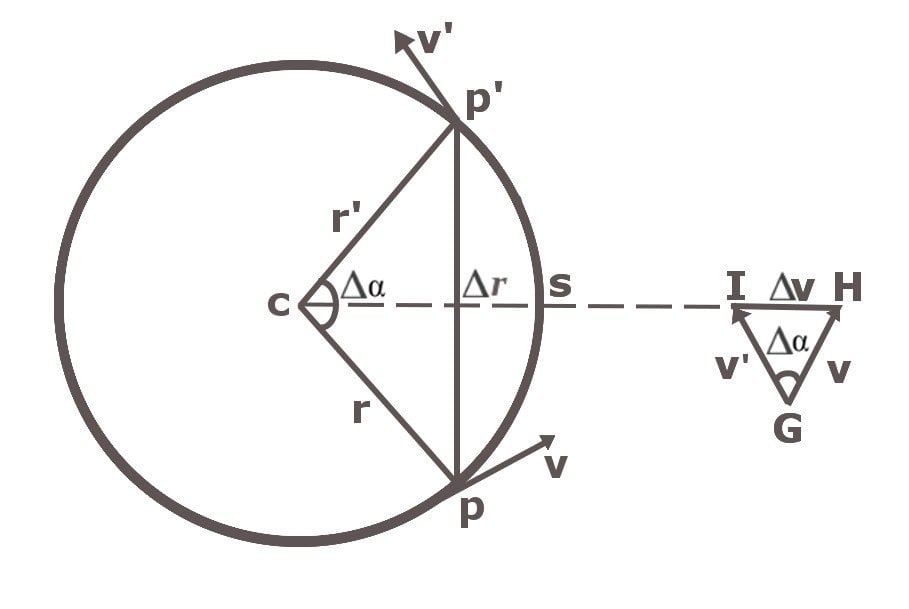
The circle represents the circular trajectory of a body, which at point P has a linear velocity v, and later, at point P’, has a linear velocity v’. Observe how the velocities are tangential to the two points, and therefore perpendicular to the radii r and r’ by which they are tethered to the center. Logically, then, the change in velocity Δv is also perpendicular to the change in radius Δr. As a consequence, the centripetal acceleration a(c), which is directed towards the change in velocity Δv, is also perpendicular to Δr. One can infer from the diagram that a line bisecting Δr perpendicularly goes through the center of the circle. This can also be illustrated with a triangle of vectors. Observe the small triangle drawn adjacent to our circle: the resultant vector of v and v’ – Δv — points inward, or more precisely, towards the center of the circle. We have determined centripetal acceleration’s direction, now let’s determine its magnitude.
The two isosceles triangles – one formed by the radii and the chord (PCP), and the other formed by the velocities and the resultant (IGH) – are similar. This means that the ratios of their sides are equal. For an infinitesimally small angle α, the arc Δs becomes indistinguishable from the chord Δr. At an infinitesimally small angle, the arc becomes one of the infinitesimally small lines that together constitute the entire, huge circle. Considering that the two triangles are similar and that Δs = Δr, we find that:


Divide the two sides by Δt. The ratio Δv/Δt is equal to centripetal acceleration a(c) and the ratio Δs/Δt is equal to v. According to Newton’s second law, the force F that imparts the acceleration is a product of the body’s mass m and the acceleration a.



One can understand from this expression why taking sharp turns, particularly at a high velocity, is astonishingly difficult. In fact, the magnitude of acceleration is directly proportional not only to the magnitude of velocity, but to the square of the magnitude of velocity, which means that a car of a certain mass m, to turn when speeding at 100 km/hr, would require four times the centripetal force it would require to turn when traveling at 50 km/hr. Furthermore, the magnitude is inversely proportional to the radius of the circle the arc would have drawn; therefore, the car would require an even greater centripetal force to curve sharply. However, at least the force would be real; centripetal force really exists. Centrifugal force, on the other hand, does not.

What Is Centrifugal Force?
Centrifugal force is often referred to as the equal and opposite reaction to centripetal force. If the centripetal force issued by your hand on one end of the string makes the bucket attached to the other end whirl around you, then it is the centrifugal force that prevents the water in the bucket from spilling out. The smaller the centripetal force, or the slower you rotate the bucket, the smaller the centrifugal force, or the more liable the water is to spill due to gravity. Such an equal and opposite force is also experienced by passengers in a turning car. As the car turns left, the passengers drift to the right. However, while its effects are palpable, physicists assert that the force doesn’t really exist in nature.
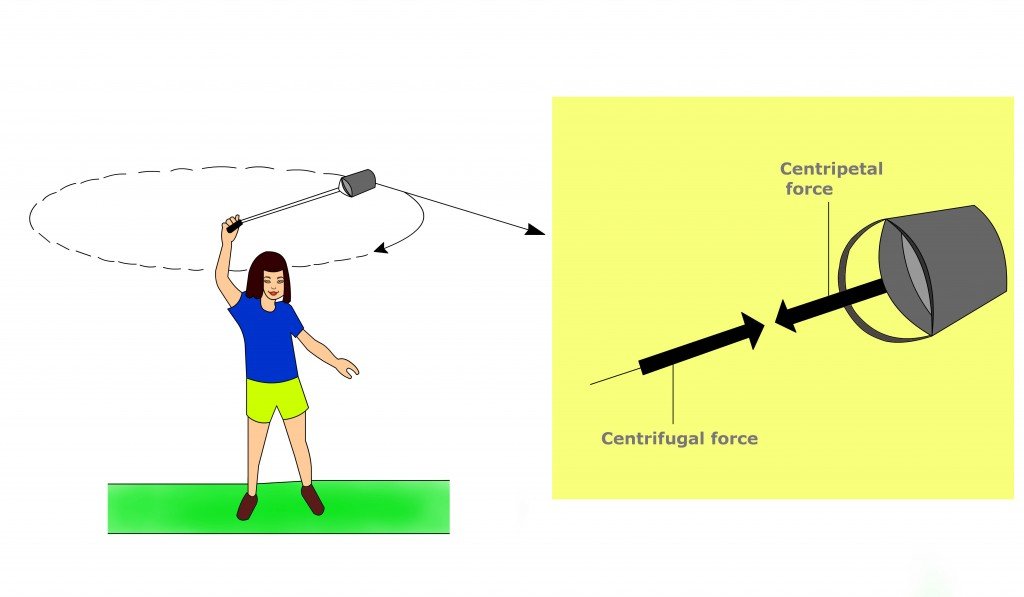
Fundamentally, there exist in the Universe only four forces: strong, weak, electromagnetic and gravitational. Every other force we encounter is actually a manifestation of one or several of these forces. For instance, remember that centripetal force is just a force that acts towards the center or constrains the motion of a body to a circle. It is the electromagnetic interactions between my fingers and the rope that cause the stone attached to its other end to whirl around me. Electromagnetic forces manifest as the centripetal force that constantly pulls the stone towards the center.
Another example of such a manifestation is our orbit around the Sun. It is the Sun’s gravitational force that pulls us towards it, the center of our practically circular orbit, thereby manifesting as centripetal force. This is why centripetal force is deemed real — it is not a new force — but instead, it is any fundamental force acting towards the center of a circle. Centrifugal force is fictitious or apparent because there is no instance where any of the four fundamental forces manifest as centrifugal force. For this reason, it doesn’t exist in nature. It is merely the inevitable consequence of how we do physics.

Merriam-Webster defines a frame of reference as “an arbitrary set of axes with reference to which the position or motion of something is described or physical laws are formulated.” A frame of reference is a system that is subjected to several forces. The problem is that a frame of reference is individualistic — the passenger and an observer observing the turning car from outside each have their own frames of reference.
A frame of reference is inertial when the forces to which it is subjected negate each other, such that the net force experienced by the system is zero, and therefore, so is the acceleration. No acceleration doesn’t necessarily mean no motion – according to Newton’s first law of motion, a system experiences no acceleration when it is either at rest or moving at a constant speed in a straight line. However, remember that even though the car turns at a constant speed – because, to trace a circle, it must change its direction constantly — it is accelerating. Such a frame of reference is therefore non-inertial.
What the passenger inhabits is a non-inertial frame of reference, or more precisely, a rotating frame. And because a non-inertial frame accelerates, it cannot exist without the presence of an additional force. This is the force that causes the passenger to feel that she is being pushed in the opposite direction. Also, because she witnesses a change in direction or trajectory (of the other passengers as well), she’s certain that some force is present. We call this force the centrifugal force.
However, the system appears drastically different to an observer observing the car from outside, or to a person inhabiting an inertial frame of reference. To such an observer, no such push is apparent. What she observes is simply the passenger moving inwards, as directed by the centripetal force — the real force generated by the friction, and more fundamentally, the electromagnetic interactions, between the tires and the road.

A centrifugal force becomes necessary and must be added to non-inertial frames, such as a rotational frame, because it makes calculations much simpler, more convenient and intuitive. A centrifugal force wouldn’t arise if we didn’t study rotational motion with a rotational frame. However, we would find the calculations to be quite tedious and cumbersome, which is why the force is a consequence of how we do physics.
In a rotational frame, it is as equal and opposite in nature as is the pull you feel when the vehicle you’re traveling in suddenly accelerates. The centrifugal force that one feels is just a consequence of one’s inertia, one’s tendency to resist a change in motion. The greater the change, the greater is the “pull”. In fact, you have surely experienced that when a vehicle suddenly accelerates to a very high velocity, the pull is seemingly impossible to overcome. This is why the water doesn’t spill when the bucket is rotated at a high velocity.

Scientists have actually found an ingenious way to exploit the force’s inertial nature. In the same way that centrifugal force pins the water to the bucket’s surface, it can also pin the passengers of a rotating spaceship to its sides and surface. If you’re wondering why the Endurance was so furiously rotating in the film Interstellar, it was doing so to simulate gravity with the centrifugal force derived through the process. The majority of NASA’s gravity-simulating prototypes “roll” ahead or “spin” in place. The merely fictitious or apparent force then emulates a real, fundamental force.