Table of Contents (click to expand)
The Buffer Capacity is a measure of resistant a particular solution is resistant to change in pH when an acid or a base is added to it.
If you remember high school chemistry or took a college course like Chemistry 101, you will have conducted a titration test. Personally, the first time I let the liquid percolate at the bottom of the glass flask, patiently waiting for the solution to turn to a tinge of pink or magenta, it honestly made me feel like a scientist! However, why does this solution change color only when a certain amount of chemicals are added? To get that answer, we must understand the inherent properties of the solution.
Recommended Video for you:
Buffer Capacity: Definition
Before we get into what a buffer capacity is, we should first understand buffers. A buffer is a compound that resists changes in pH when a limited amount of acid or base is added to it. The chemical composition of a buffer solution usually entails a weak acid or a weak base accompanied by its conjugate salt.
Now, Buffer Capacity can be defined as the measure of the efficiency of a buffer in resisting its change in pH. This definition does present a bit of a problem as to ‘what is the significant change?’ Sometimes, a change of 1 unit does not bring about any significant change. At other times, even a 0.1-unit change can cause a significant difference. So, to give a more clear definition, buffer capacity may be defined as the quantity of a strong acid or strong base that must be added to one liter of a solution to change it by one pH unit. The buffer capacity equation is as follows: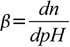
where n is some equivalents of added strong base (per 1 L of the solution). Note that the addition of n moles of acid will change the pH by the same value, but in the opposite direction. We will derive a formula connecting buffer capacity with pH, pKa and buffer concentration.
Calculation Of Buffer Capacity
Now that we have seen how the buffer equation can be written, let’s try to derive it to have a better understanding of how we arrived at the above equation. To make this derivation a bit easier, we shall make the base monoprotic (a base that will accept only one proton). We shall also assume the volume to be one, as this helps us treat concentration and the number of moles interchangeably. The charge balance of the solution we assume is demonstrated by the following equation:
[A–]+[OH+]=[B+]+[H+]
[B+] denotes the presence of a strong base concentration in the solution. The [B+] is also the n present in the first buffer capacity equation. Now the total concentration of the buffer is given by the following equation:
Cbuff =[HA]+[A–]
The [AH] in the above equation can be broken down into smaller constituent elements. This breaking down of a larger, more complex compound into smaller basic elements is known as the dissociation constant. The dissociation constant helps in the easier simplification of the derivation. The Ka in the below equation is the acid dissociation constant. It relates to how easily a molecule will act as an acid.
[HA]=([H+][A–])/Ka
Now, the above equation can be substituted in the buffer concentrate equation, giving the following equation:
Cbuff= ([H+][A–])/Ka + [A–]
Now, if we were to take [A–] as a common factor and LCM to simplify the above equation, we would get the following equation:
[A–]= (Cbuff+Ka)/(Ka+H+)
Before moving forward, we must understand one critical definition that will serve as a prerequisite to neatly wrap this derivation up, known as the water ionization constant or the self-ionization of water. The self-ionization of water is an ionization reaction that occurs in pure water or in an aqueous solution, in which H2O loses the nucleus of one of its hydrogen atoms to become a hydroxide ion, OH−.
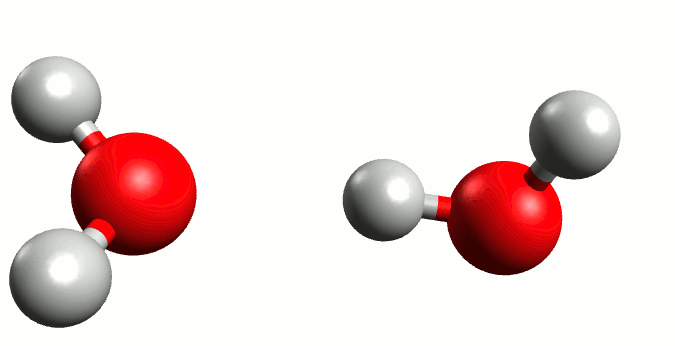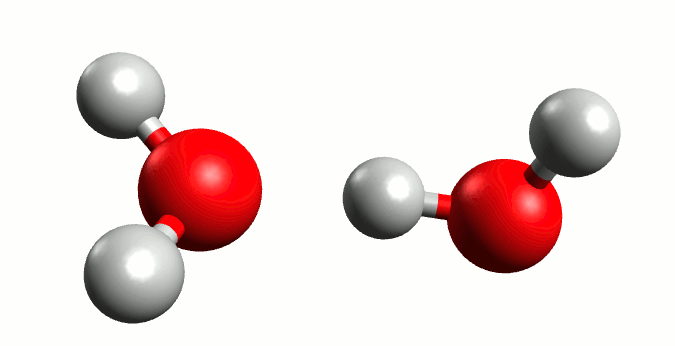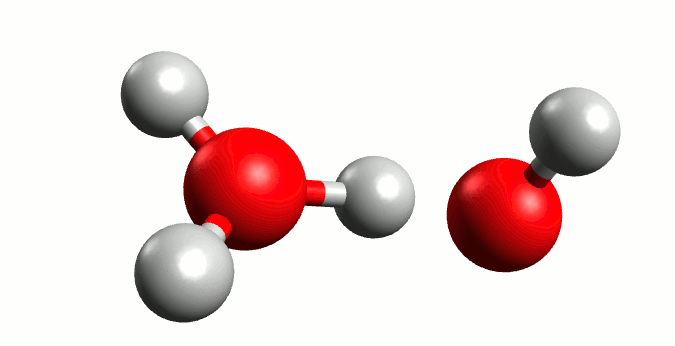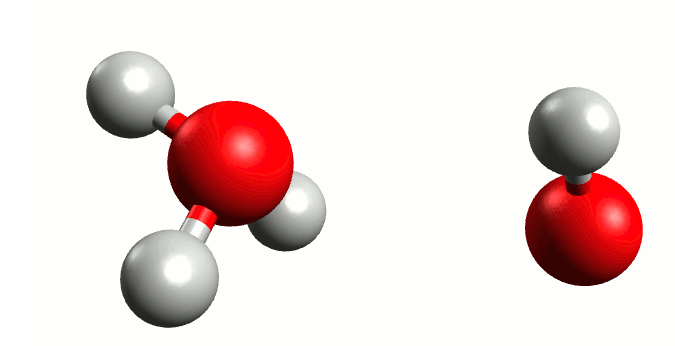
Now, using the charge balance equation, the [A–] equivalent and the water ionization constant, we can come to the following equation:
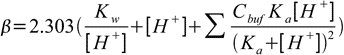The first two terms present in the equation are not dependent on the buffer in the solution. They represent the fact that the solution of high (or low) pH is resistant to pH changes. This indicates that certain solutions with extremities in pH are resistant to changes, even without a buffer solution present.
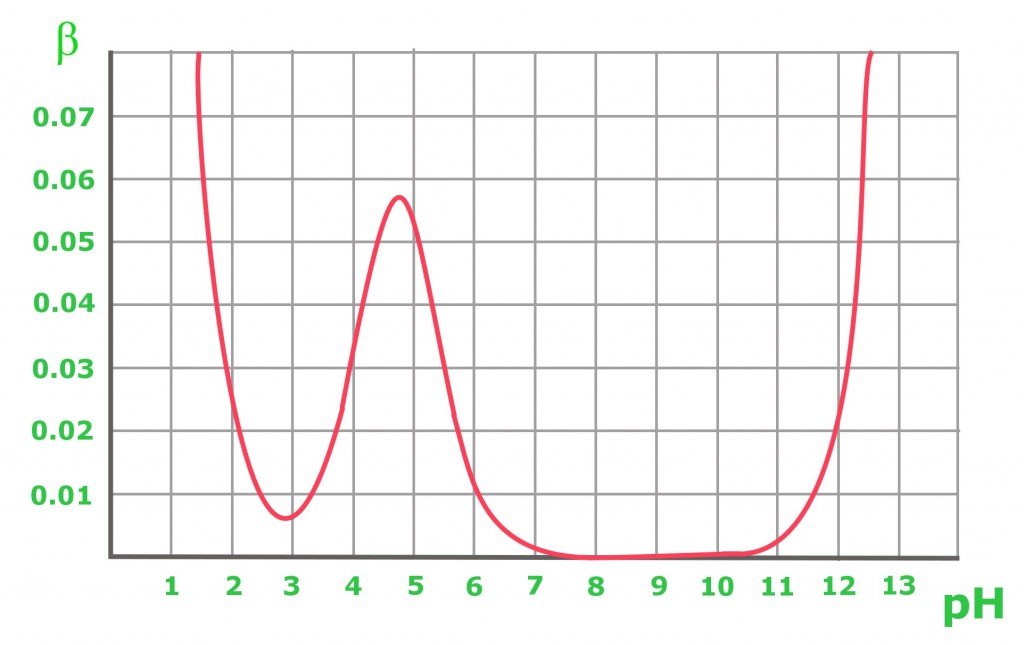The graph above shows the buffer capacity changes in 0.1 M of an acetic buffer. As expected, the buffer resists acid and base addition to maintain an equimolar solution (when pH=pKa). From the graph, it is obvious that the buffer capacity has reasonably high values only for pH close to the pKa value: the further from the optimal value, the lower the buffer capacity of the solution. A solution containing a conjugate base of pH 8-10 has a buffer capacity of zero, while for a higher pH, the presence of the strong base starts to play an important role. In the case of a pure acetic acid solution with a pH below 3, the pH is already low enough to be resistant to changes due to the high concentration of H+ cations.
